一、数据说明
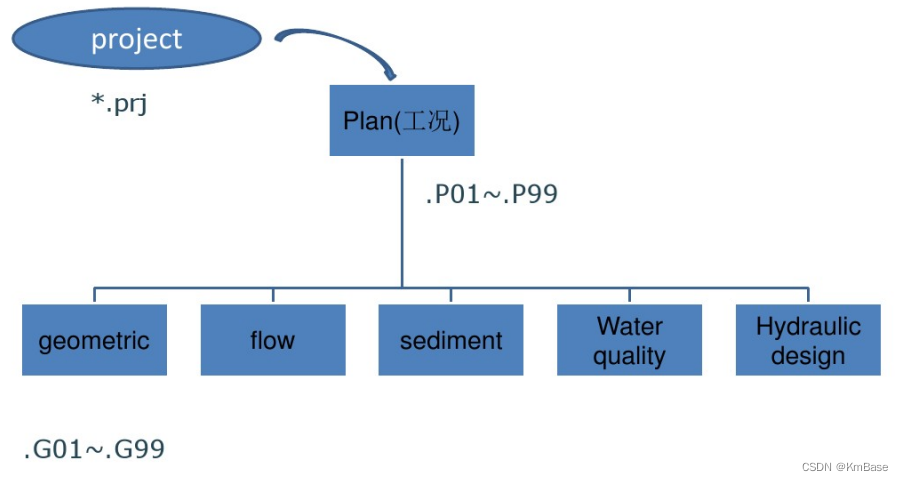
HEC-RAS模型主要由工程文件 (.prj) 文 件 、 河道地形数据文件 ( .g01)、运行文件(p01)、非恒定流文件 ( .u01) 等部分组成。
1. 一般数据
在创建并保存project文件(*.prj)后,其他data文件均会自动以同样的名字保存,但采用不同的后缀来区分各类文件。
"字母+数字"的后缀方案:主要的data命名规则如下:
- One file for each Plan(.P01 to.P99)
- One Run file for each unsteady flow plan(.X01 to .X99)
- One Output file for each plan(.001 to .099)
- One file for each set of Geometry data(.G01 to .G99)
- One file for each set of Unsteady Flow data(.U01 to .U99)
2. 一维几何数据
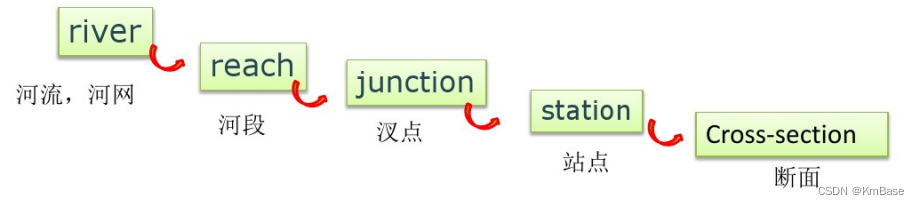
- 每个河网由一个或多个河段(reach)相互连接而成,汇合处称为汊点(junction)。
- Reach以reach name彼此区分,每个reach还有一个其所在河流的river name。
- 以river为单位(注意不是reach)从下游向上游定义距离空间,每个river上的位置都对应于一个数值,即station,自上游往下游数值由大到小,标示断面所处的位置,但数值大小在具体计算中并无意义。
3. 几何数据方向
HecRas中的river线、cross section线都是具有方向的,river线需要从上游向下游绘制,cross section线需从左岸向右岸绘制。
二、一维恒定流原理
1. 概念
如果液体流动时,空间各点处的所有水力要素都不随时间变化,那么这股液体就是恒定流。液体运动时的空间各点的运动要素不随时间发生变化,而不是各点的空间要素相同。
恒定流计算的一些假定
- 流动是恒定的
- 流动是渐变的
- 流动是一维的
- 渠道底坡比较缓,小于1:10
2. 基本原理
能量守恒
Z 2 + Y 2 + α 2 V 2 2 2 g = Z 1 + Y 1 + α 1 V 2 1 2 g + h e Z_2+Y_2+\frac {\alpha _{2}V_{2}^{2}}{2g}=Z_1+Y_1+\frac {\alpha _{1}V_{2}^{1}}{2g}+h_e Z2+Y2+2gα2V22=Z1+Y1+2gα1V21+he
其中 Z Z Z为地面高程, Y Y Y为水深, α V 2 2 g \frac {\alpha V^{2}}{2g} 2gαV2为流速水头, h e h_e he为能量损失由沿程和局部两部分组成.

能量损失
h e = L S ‾ f + C ( α 2 V 2 2 2 g − α 1 V 1 2 2 g ) h_e = L \overline S_{f}+C(\frac {\alpha_{2} V_{2}^{2}}{2g}-\frac {\alpha_{1} V_{1}^{2}}{2g}) he=LSf+C(2gα2V22−2gα1V12)
式中 L L L为流程长, S ‾ f \overline S_{f} Sf为比阻, C C C为局部阻力系数
L = L l o b Q ‾ l o b + L c h Q ‾ v h + L r o b Q ‾ l o b Q ‾ l o b + Q ‾ c h + Q ‾ r o b L=\frac {L_{lob}\overline Q_{lob}+L_{ch}\overline Q_{vh}+L_{rob}\overline Q_{lob}}{\overline Q_{lob}+\overline Q_{ch}+\overline Q_{rob}} L=Qlob+Qch+QrobLlobQlob+LchQvh+LrobQlob
式中 L l o b 、 L c h 、 L r o b L_{lob}、L_{ch}、L_{rob} Llob、Lch、Lrob为断面分别到左岸、河槽和右岸的指定长度; Q ‾ l o b 、 Q ‾ c h 、 Q ‾ r o b \overline Q_{lob}、\overline Q_{ch}、\overline Q_{rob} Qlob、Qch、Qrob为断面到左岸、河槽和右岸的平均流量。
断面过流能力计算
Q = K S f 1 / 2 Q=KS_{f}^{1/2} Q=KSf1/2 K = 1.486 n A R f 2 / 3 K=\frac{1.486}{n}AR_{f}^{2/3} K=n1.486ARf2/3
式中 K K K为流量模数; n n n为曼宁系数; A A A过水面积; R R R水力半径; S ‾ f \overline S_{f} Sf为比阻,即水力坡度 i i i。
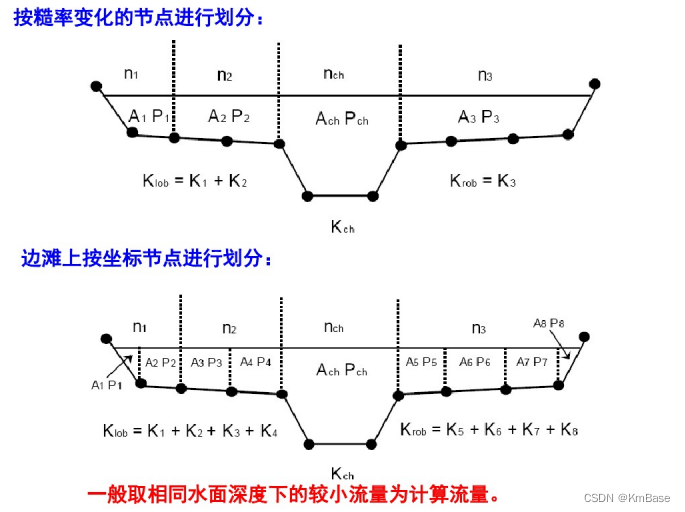
左岸,主槽,右岸采用不同的参数进行计算,三部分相加获得整个断面的流量模数。计算可给出各部分流量的分配结果。
程序将河堤中所有增量流量相加,得到左岸和右岸的流量。主河槽流量通常按流量单元计算。截面的总流量是通过将三个细分流量(左、河槽和右)相加得到的。
HEC-RAS中可用的另一种方法是计算边滩中每个坐标点之间的流量(见下图)。然后对流量求和,得到总的左边滩值和右边滩值。该方法用于美国陆军陆战队HEC-2项目。该方法保留为HEC-RAS内的一个选项,以重现最初与HEC-2一起开发的研究。
当覆盖河岸上的部分有具有显著垂直坡度的地面部分时,这两种计算流量的方法将产生不同的答案。一般来说,HEC-RAS默认方法在相同的水面标高下,流量较小。
一般来说,我们认为HEC-RAS的默认方法更符合曼宁公式和流量单元的概念。需要对观察到的水面线进一步研究,才能对这两种方法的准确性做出结论。
糙率系数的选择
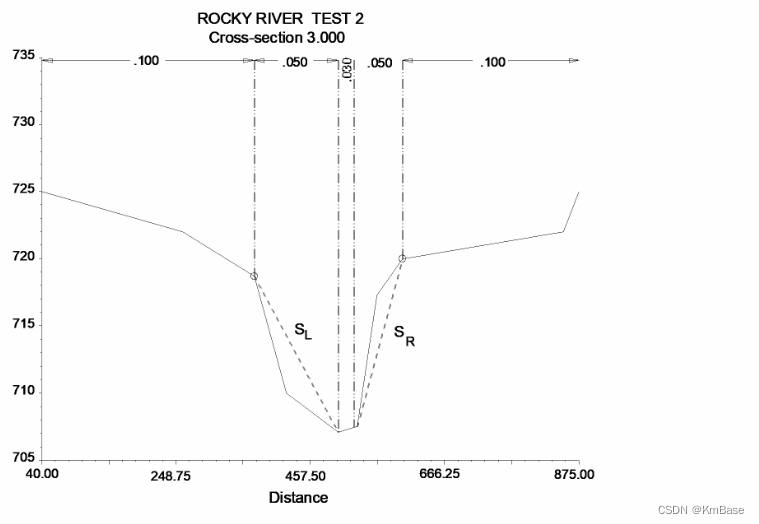
当主槽边坡大于5H:1V,或是主槽有多个糙率的情况,按各部分湿周加权计算得出一个复合糙率:
n c = [ ∑ i = 1 N ( P i n i 1.5 ) P ] 2 / 3 n_c=\left [ \frac {\sum_{i=1}^{N}(P_{i}n_{i}^{1.5})}{P} \right ] ^{2/3} nc=[P∑i=1N(Pini1.5)]2/3
式中 n c n_c nc为复合或等效粗糙系数; P P P为整个主槽的湿周和; P i P_{i} Pi第i个湿周; n i n_{i} ni第i个湿周对应的糙率。
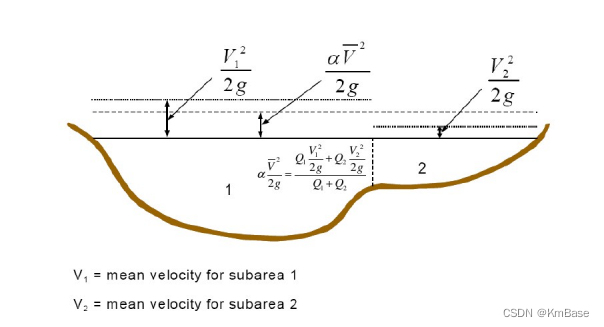
断面平均动能
在1D河段内,每个横截面仅计算单个水面,因此计算单个平均能量。对于给定的水面高程,通过计算横截面三个分段(左岸、主河槽和右岸)的流量加权能量来获得平均能量。下图显示了如何获得具有主河道和右边滩(无左侧边滩)的横截面的平均能量。
α \alpha α为流速系数,按下式计算
α = [ Q 1 V 1 2 + Q 2 V 2 2 + ⋯ Q N V N 2 ] Q V ˉ 2 \alpha=\frac{\left[Q_{1} V_{1}^{2}+Q_{2} V_{2}^{2}+\cdots Q_{N} V_{N}^{2}\right]}{Q \bar{V}^{2}} α=QVˉ2[Q1V12+Q2V22+⋯QNVN2]
也可以用流量模数和面积表示
α = ( A t ) 2 [ K l o b 3 A obb + K c h 3 A c h 2 + K r o b 3 A r o b 2 ] K t 3 \alpha=\frac{\left(A_{t}\right)^{2}\left[\frac{K_{l o b}^{3}}{A_{\text {obb }}}+\frac{K_{c h}^{3}}{A_{c h}^{2}}+\frac{K_{r o b}^{3}}{A_{r o b}^{2}}\right]}{K_{t}^{3}} α=Kt3(At)2[Aobb Klob3+Ach2Kch3+Arob2Krob3]
阻力系数(水力坡度)

水面线计算
- 对于缓流,在上游断面假定一个水深;
- 若是急流,则在下游断面假定一个水深;
- 基于假定的水位,确定对应的总输水流量和速度水头;· 计算损失;
- 求解WS(水面);
- 计算值和估计值进行比较,满足要求即停止;
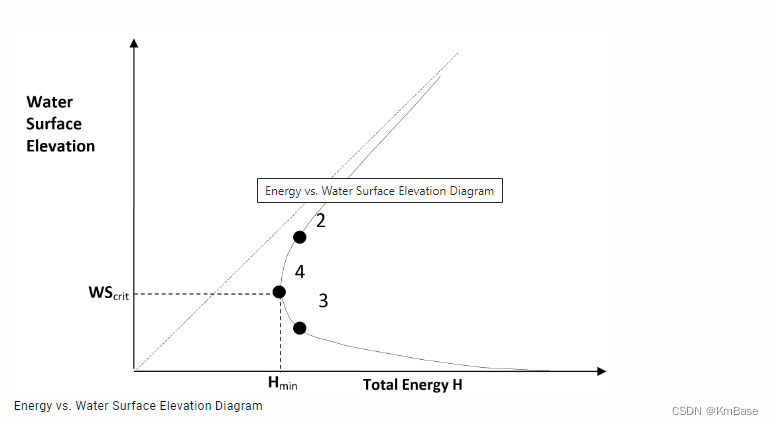
临界水深计算
确定流动是急流还是缓流,便于采用合适的计算方法,并进行流动分析。计算中一般自动计算该项。
断面的总能量:
H = W S + V 2 2 g H=WS+\frac {V^2}{2g} H=WS+2gV2
临界水深的计算方法:
- 抛物线法 对于单个极值
- 割线法 对于多个极值
假定水面高程,采用上述方程获得最小的能量值所对应的临界水深。
动量方程的应用
能量方程适用于渐变流的情况。当水面从急流-缓流,以及缓流-急流的情况下,即在急变流的情况下,如渠道底坡的急剧变化如有水跃发生、通过桥梁、堰、河网节点等情况,能量方程不再使用,此时可采用经验公式,但很多情况下必须采用动量方程加以求解。
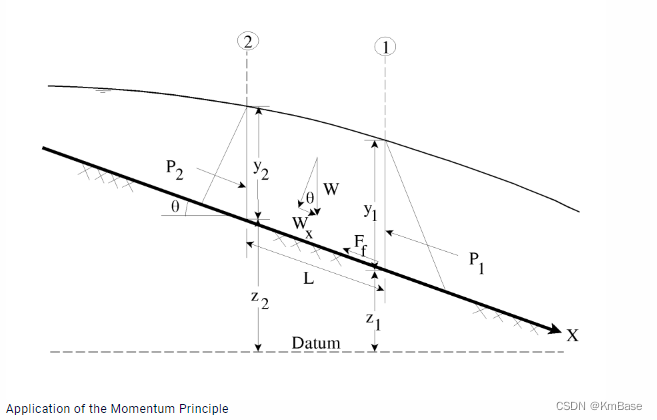
牛顿第二定律:
∑ F x = m a \sum F_{x}=ma ∑Fx=ma
代入各项力,即得:
P 2 − P 1 + W x − F x = Q ρ Δ V x P_2-P_1+W_x-F_x=Q\rho\Delta V_{x} P2−P1+Wx−Fx=QρΔVx
P 2 − P 1 P_2-P_1 P2−P1为压力项,1、2处的静水压力差; W x W_{x} Wx为重力项, − F x -F_{x} −Fx阻力项, Δ V x \Delta V_{x} ΔVx为x方向的流速变化。
HEC-RAS中所用的动量方程形式:
Q 2 2 β 2 g A 2 + A 2 Y ˉ 2 + A 1 + A 2 2 L S 0 − A 1 + A 2 2 L S ˉ f = Q 1 2 β 1 g A 1 + A 1 Y ˉ 1 \frac{Q_2^2\beta_2}{gA_2}+A_2\bar{Y}_2+\frac{A_1+A_2}{2}LS_0-\frac{A_1+A_2}{2}L\bar{S}_f=\frac{Q_1^2\beta_1}{gA_1}+A_1\bar{Y}_1 gA2Q22β2+A2Yˉ2+2A1+A2LS0−2A1+A2LSˉf=gA1Q12β1+A1Yˉ1
其中, β \beta β为动量系数; L L L为断面1、2距离; S 0 S_{0} S0为河底坡度; S ˉ f \bar{S}_f Sˉf为水力坡度; Y Y Y为水面到横截面积质心的深度。
高速掺气水流
对于高流速河流,由于水体掺气,水面可能略高于其他预期,特别是弗劳德数大于1.6时。HEC-RAS考虑了这一点。
弗劳德数 F ≥ 8.2 F\ge8.2 F≥8.2时:
D a = 0.906 D ( e ) 0.061 F D_a=0.906D(e)^{0.061F} Da=0.906D(e)0.061F
弗劳德数 F ≤ 8.2 F\le8.2 F≤8.2时:
D a = 0.620 D ( e ) 0.1051 F D_a=0.620D(e)^{0.1051F} Da=0.620D(e)0.1051F
其中, D a D_a Da为掺气水深; D D D为不考虑掺气的水深; e e e为自然常数, 2.718282; F F F为弗劳德数。
三、一维非恒定流原理
1. 概念
如果液体流动时,空间各点处的水力要素随时间变化,那么这股液体就是非恒定流。
2. 基本原理
连续性方程:
∂ A T ∂ t + ∂ Q ∂ x = q t \frac {\partial A_T}{\partial t}+\frac {\partial Q}{\partial x}=q_t ∂t∂AT+∂x∂Q=qt
动量方程:
∂ Q ∂ t + ∂ ( Q V ) ∂ x + g A ( ∂ z s ∂ x + S f ) = 0 \frac {\partial Q}{\partial t}+\frac {\partial (QV)}{\partial x}+gA(\frac{\partial z_{s}}{\partial x}+S_f)=0 ∂t∂Q+∂x∂(QV)+gA(∂x∂zs+Sf)=0
3. 公式推导
连续性方程
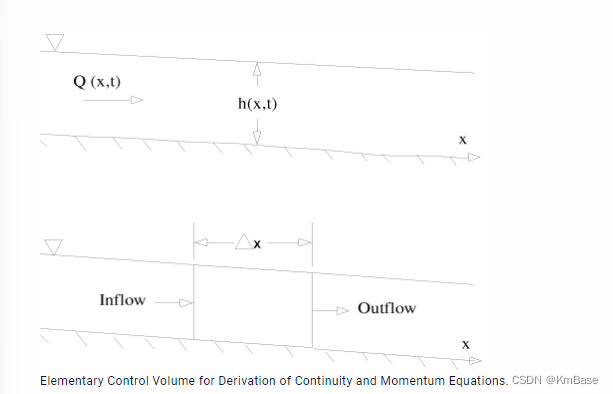
单位时间 Δ x \Delta x Δx河段入流为:
Q − ∂ Q ∂ x Δ x 2 Q-\frac {\partial Q}{\partial x}\frac {\Delta x}{2} Q−∂x∂Q2Δx
出流为:
Q + ∂ Q ∂ x Δ x 2 Q+\frac {\partial Q}{\partial x}\frac {\Delta x}{2} Q+∂x∂Q2Δx
从流量单位体积变化求得控制体体积为:
∂ A T ∂ t Δ x \frac {\partial A_T}{\partial t}\Delta x ∂t∂ATΔx
假设 Δ x \Delta x Δx很小,控制体中的质量变化为:
ρ ∂ A T ∂ t Δ x = ρ [ ( Q − ∂ Q ∂ x Δ x 2 ) − ( Q + ∂ Q ∂ x Δ x 2 ) + Q l ] \rho \frac {\partial A_T}{\partial t}\Delta x=\rho \left[(Q-\frac {\partial Q}{\partial x}\frac {\Delta x}{2})-(Q+\frac {\partial Q}{\partial x}\frac {\Delta x}{2})+Q_l\right] ρ∂t∂ATΔx=ρ[(Q−∂x∂Q2Δx)−(Q+∂x∂Q2Δx)+Ql]
其中, Q l Q_l Ql为侧向流, ρ \rho ρ为流体密度。
化简后得到:
∂ A T ∂ t + ∂ Q ∂ x = q t \frac {\partial A_T}{\partial t}+\frac {\partial Q}{\partial x}=q_t ∂t∂AT+∂x∂Q=qt
其中, q t q_t qt为单位长度的侧向流。
动量方程

根据牛顿第二定律:
∑ F x = m a \sum F_{x}=ma ∑Fx=ma
动量(MV)是流体质量乘以流动方向上的速度矢量。将考虑三种力:(1)压力,(2)重力,(3)边界阻力,或摩擦力。
控制体积的压力之和为:
F P n = − ρ g A ∂ h ∂ x Δ x (1) F_{Pn}=−ρgA\frac {\partial h}{\partial x}\Delta x \tag{1} FPn=−ρgA∂x∂hΔx(1)
控制体积内流体在x方向上的重力为:
F g = − ρ g A ∂ z 0 ∂ x Δ x (2) F_g=−ρgA\frac{∂z_0}{∂x}Δx\tag{2} Fg=−ρgA∂x∂z0Δx(2)
边界阻力的以下表达式:
F s = − ρ g A S f Δ x (3) F_s=-ρgAS_fΔx\tag{3} Fs=−ρgASfΔx(3)
其中,水力坡度摩擦斜率必须与流量和水位有关。传统上,使用Manning和Chezy摩擦方程。曼宁公式可以写成:
S f = Q ∣ Q ∣ n 2 2.208 R 4 / 3 A 2 S_f=\frac{Q|Q|n^2}{2.208R^{4/3}A^2} Sf=2.208R4/3A2Q∣Q∣n2
流入控制体积的通量可以写成:
ρ [ Q V − ∂ Q V ∂ x Δ x 2 ] \rho \left[QV-\frac{\partial QV}{\partial x}\frac {\Delta x}{2}\right] ρ[QV−∂x∂QV2Δx]
流出控制体积的通量可以写成:
ρ [ Q V + ∂ Q V ∂ x Δ x 2 ] \rho \left[QV+\frac{\partial QV}{\partial x}\frac {\Delta x}{2}\right] ρ[QV+∂x∂QV2Δx]
因此,进入控制体积的动量净速率(动量通量)为:
− ∂ Q V ∂ x Δ x (4) -\frac{\partial QV}{\partial x} {\Delta x}\tag{4} −∂x∂QVΔx(4)
由于流体在控制体积中的动量为ρQΔx,动量的积累速率可写成
∂ ∂ t ( ρ Q Δ x ) = ρ Δ x ∂ Q ∂ t (5) \frac {\partial}{\partial t}(\rho Q\Delta x)=\rho \Delta x\frac {\partial Q}{\partial t}\tag{5} ∂t∂(ρQΔx)=ρΔx∂t∂Q(5)
进入体积(4)的动量的净速率(动量通量)加上作用在体积上的所有外力的总和[(1)+(2)+(3)]等于动量的累积速率(5)。因此
ρ Δ x ∂ Q ∂ t = − ρ ∂ Q V ∂ x Δ x − ρ g A ∂ h ∂ x Δ x − ρ g A ∂ z 0 ∂ x Δ x − ρ g A S f Δ x \rho \Delta x\frac {\partial Q}{\partial t}=-\rho\frac{\partial QV}{\partial x} {\Delta x}−ρgA\frac {\partial h}{\partial x}\Delta x−ρgA\frac{∂z_0}{∂x}Δx-ρgAS_fΔx ρΔx∂t∂Q=−ρ∂x∂QVΔx−ρgA∂x∂hΔx−ρgA∂x∂z0Δx−ρgASfΔx
由于水面高程 z z z等于 z 0 + h z_0+h z0+h,因此:
∂ z z ∂ x = ∂ h ∂ x + ∂ z 0 ∂ x \frac{∂z_z}{∂x}=\frac{∂h}{∂x}+\frac{∂z_0}{∂x} ∂x∂zz=∂x∂h+∂x∂z0
合并上述两式,简化后可得:
∂ Q ∂ t + ∂ ( Q V ) ∂ x + g A ( ∂ z s ∂ x + S f ) = 0 \frac {\partial Q}{\partial t}+\frac {\partial (QV)}{\partial x}+gA(\frac{\partial z_{s}}{\partial x}+S_f)=0 ∂t∂Q+∂x∂(QV)+gA(∂x∂zs+Sf)=0
四、一维非恒定流方程离散形式及求解
1. HEC-RAS中使用的连续性方程和动量方程
HEC-RAS模型考虑河漫滩储水条件下的河道水流连续性方程为:
∂ A T ∂ t + ∂ S ∂ t + ∂ Q ∂ x = q t \frac {\partial A_T}{\partial t}+\frac {\partial S}{\partial t}+\frac {\partial Q}{\partial x}=q_t ∂t∂AT+∂t∂S+∂x∂Q=qt
其中, S S S为漫滩储水
动量方程为:
∂ Q ∂ t + ∂ ( Q V ) ∂ x + g A ( ∂ z s ∂ x + S f ) = 0 (1) \frac {\partial Q}{\partial t}+\frac {\partial (QV)}{\partial x}+gA(\frac{\partial z_{s}}{\partial x}+S_f)=0\tag{1} ∂t∂Q+∂x∂(QV)+gA(∂x∂zs+Sf)=0(1)
∂ Q c ∂ t + ∂ ( Q c V c ) ∂ x c + g A c ( ∂ z s ∂ x c + S f c ) = M f (2) \frac {\partial Q_c}{\partial t}+\frac {\partial (Q_cV_c)}{\partial x_c}+gA_c(\frac{\partial z_{s}}{\partial x_c}+S_{fc})=M_f\tag{2} ∂t∂Qc+∂xc∂(QcVc)+gAc(∂xc∂zs+Sfc)=Mf(2)
∂ Q f ∂ t + ∂ ( Q f V f ) ∂ x f + g A f ( ∂ z s ∂ x f + S f f ) = M c (3) \frac {\partial Q_f}{\partial t}+\frac {\partial (Q_fV_f)}{\partial x_f}+gA_f(\frac{\partial z_{s}}{\partial x_f}+S_{ff})=M_c\tag{3} ∂t∂Qf+∂xf∂(QfVf)+gAf(∂xf∂zs+Sff)=Mc(3)
其中,Mc和Mf分别是河道和漫滩之间单位距离交换的动量通量。注意,在(2)和(3)中,水面高程没有下标。这些方程中的一个假设是,在垂直于水流的任何横截面上,水面都是水平的。因此,在给定横截面上,河道和漫滩的水面高程相同。
2. 方程离散形式及求解
HEC-RAS模型在河流汊点处通过连续性方程和能量方程进行衔接:
连续性方程:
∑ i = 1 l S g i Q i = 0 \sum _{i=1}^{l}S_{gi}Q{i}=0 i=1∑lSgiQi=0
式中, l l l为连入同一汊点河流的数量; S g Sg Sg为-1时,表示支流 i i i流入汊点;Sgi 为1时,表示支流 i i i流出汊点;Q, 为支流 i i i的流量。
能量方程:
z 1 = z c z_1= z_c z1=zc
式中, z 1 z_1 z1为支流 k k k汉点边界水位; z c z_c zc河流汉点处的边界水位。
HEC-RAS模型应用Preissmann 四点隐式有限差分法对连续性方程和运动方程进行求解。
Preissmann隐式差分格式如图所示,它是一种四点偏心隐式格式,因此也称四点隐式差分法,是普莱士曼 (Preissmann)1961年提出,它主要是对因变量 f f f及其一阶偏微商在相邻点和相邻时间层采用加权平均进行离散,即对时间 t t t的偏微商分别取点 j j j和 j + 1 j+1 j+1 的差商平均值,对空间 x x x的偏微商则是分别取 n △ t n△t n△t和 ( n + 1 ) △ t (n+1)△t (n+1)△t时间层的差商加权平均值,因变量 f f f采用同一网格周围四个相邻点的加权平均值进行逼近。
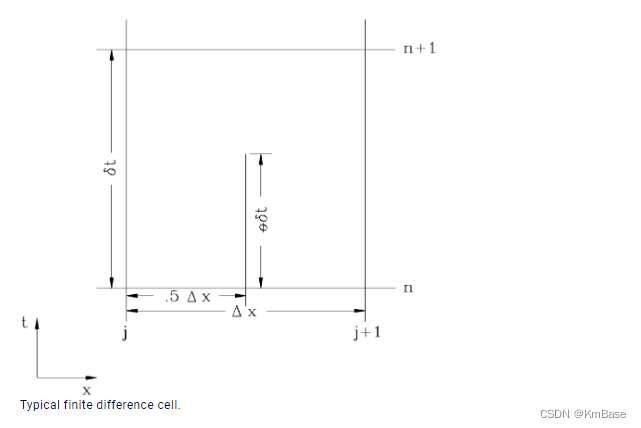
对于任意因变量及其导数可以写成如下的差分格式:
∂ f ∂ t ≈ Δ f Δ t = 0.5 ( Δ f j + 1 + Δ f j ) Δ t \frac {\partial f}{\partial t}\approx \frac {\Delta f}{\Delta t}=\frac{0.5(\Delta f_{j+1}+\Delta f_{j})}{\Delta t} ∂t∂f≈ΔtΔf=Δt0.5(Δfj+1+Δfj) ∂ f ∂ x ≈ Δ f Δ x = ( Δ f j + 1 − Δ f j ) + θ ( Δ f j + 1 − Δ f j ) Δ x \frac {\partial f}{\partial x}\approx \frac {\Delta f}{\Delta x}=\frac{(\Delta f_{j+1}-\Delta f_{j})+\theta(\Delta f_{j+1}-\Delta f_{j})}{\Delta x} ∂x∂f≈ΔxΔf=Δx(Δfj+1−Δfj)+θ(Δfj+1−Δfj) f ≈ f ‾ = ( Δ f j + 1 + Δ f j ) + 0.5 θ ( ( Δ f j + 1 + Δ f j ) f\approx \overline f=(\Delta f_{j+1}+\Delta f_{j})+0.5\theta((\Delta f_{j+1}+\Delta f_{j}) f≈f=(Δfj+1+Δfj)+0.5θ((Δfj+1+Δfj)
基于以上差分格式,对圣维南方程组进行离散化和线性化处理,得到连续性方程和运动方程:
C Q 1 j Δ Q j + C Z 1 j Δ z j + C Q 2 j Δ Q j + 1 + C Z 2 j Δ z j + 1 = C B j (4) CQ_{1j}\Delta Q_j+CZ_{1j}\Delta z_j+CQ_{2j}\Delta Q_{j+1}+CZ_{2j}\Delta z_{j+1}=CB_j\tag{4} CQ1jΔQj+CZ1jΔzj+CQ2jΔQj+1+CZ2jΔzj+1=CBj(4) M Q 1 j Δ Q j + C Z 1 j Δ z j + M Q 2 j Δ Q j + 1 + M Z 2 j Δ z j + 1 = M B j (5) MQ_{1j}\Delta Q_j+CZ_{1j}\Delta z_j+MQ_{2j}\Delta Q_{j+1}+MZ_{2j}\Delta z_{j+1}=MB_j\tag{5} MQ1jΔQj+CZ1jΔzj+MQ2jΔQj+1+MZ2jΔzj+1=MBj(5)
第 j j j差分网格中连续性方程(4)和运动方程方程(5)组成的方程组,该方程组对于河段数为m的计算河流可以建立 m m m个连续方程和 m m m个运动方程,而 m m m个河段有 m + 1 m+1 m+1个断面,每个断面中有流速、水位两个未知数,总计为 2 ( m + 1 ) 2(m+1) 2(m+1)个未知数,但可以根据上下游边界条件补充建立2个方程,就有 2 ( m + 1 ) 2(m+1) 2(m+1)个方程,于是便可以联立方程组进行求解。
应用差分格式对微分方程组进行离散化,用差商代替微分,待求方程组便由微分形式转化为差商形式,故可以通过对线性方程组进行求解实现对原微分方程组求解。现在普遍应用追赶法对上述方程组求解,在应用该方法时应考虑迭代的收敛性和稳定性。当求得的差分方程精确解为 x x x",在计算河段任意点 ( j , n ) (j,n) (j,n)上,当离散差分格的步长 ( △ x ,△ t ) (△x,△t) (△x,△t)趋于零时,只有差分方程组精确解趋近于微分方程组的解,方程组便收敛。求解线性方程组的解是逐点计算的,当计算过程中所引入的误差随时间和空间步长的变长而不断积累,最终差分方程的解被引入的误差所“淹没”,则这种数值解是不稳定的。应用Preissmann四点隐式有限差分法得到的差分方程,对于系数θ的任意值,具有对 △ x △x △x的一阶精度, θ = 0.5 θ=0.5 θ=0.5 时,具有二阶精度,当 0.5 < θ ≤ 1 0.5<θ≤1 0.5<θ≤1时,差分格式是稳定的。
参考文献:
曾玉红:Hec_RAS应用
HEC-RAS模型官方文档