目录
1. 多元高斯分布
1.1 标准高斯分布
1.2 一元高斯函数（一元高斯分布概率密度）
1.3 多元高斯分布
2. 协方差矩阵的计算
2.1 问题定义
2.2 室内外温度的例子
参考：
1. 多元高斯分布
1.1 标准高斯分布
标准高斯函数（正态分布）的标准形式有：
这个函数描述了变量x xx的一种分布特性，即为标准正态分布 x ∼ N ( 0 , 1 ) x\sim N(0,1)x∼N(0,1)，变量x xx的分布有如下特点：
- 均值为 0
- 方差为 1
- 概率密度和为 1
1.2 一元高斯函数（一元高斯分布概率密度）
一元高斯函数一般形式为：
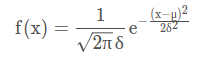
1.3 多元高斯分布
参考：数学_多元高斯分布_数学表达公式_惊鸿一博的博客-CSDN博客
回到多元正态分布，先从各维度不相关的多元高斯（正态）分布入手，数据点通过 d 维的列向量描述
，各个维度的均值方差分别为
来描述，高斯概率密度函数可以表示为：
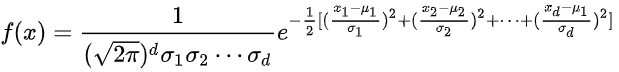
前面多出的项是为了让概率之和为1，其实这个方程可以这样子去解读：
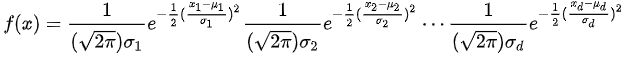
这样，各个维度之间不相关的多元正态分布概率密度其实就是各个维度的正态分布概率密度函数的乘积，其实是因为各变量之间互不相关，因此联合概率密度等于各自概率密度的乘积，我们来把她写的漂亮点：
其中， 
是协方差矩阵，里面的第 i 行第 j 列元素表示第 i 个变量第 j 个变量的协方差，由于假设了各个维度之间不相关，因此协方差矩阵只有在对角线的位置有值，代表不同变量的方差大小。这里面用到了 
（行列式的计算，对角行列式等于对角线上元素的乘积）。
2. 协方差矩阵的计算
2.1 问题定义
x为多维变量（SLAM问题中待求解的状态量），当求解x时，会用到协方差矩阵。当待求解的状态量（未知数）维数很大时，对应的协方差矩阵也很大，导致矩阵计算的计算量巨大。对于服从高斯分布的状态量，可以使用条件概率将有相关性的变量变成条件独立的情况，然后利用贝叶斯公式对求解过程进行简化，这个过程就用到了信息矩阵（协方差矩阵的逆）的边缘化。
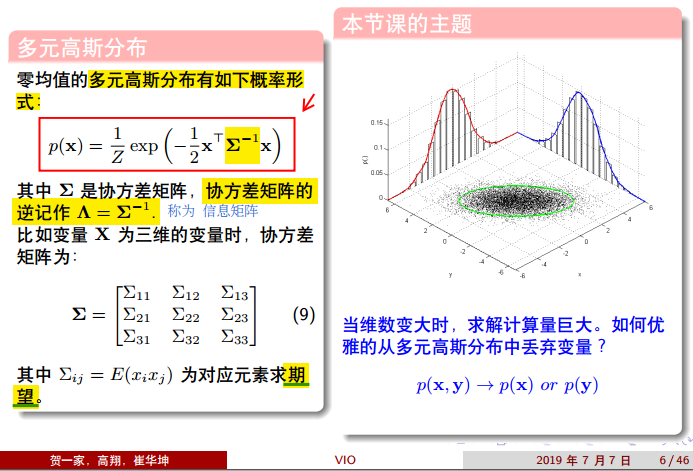
2.2 室内外温度的例子
a. 定义3个变量x1,x2,x3, 以及其表达式，假设其值服从高斯分布：
b. 根据协方差的公式 （其实就是计算期望），计算协方差矩阵中的各个元素（3x3=9个）：
c. 根据联合高斯分布求解信息矩阵（协方差矩阵的逆）：
d. 根据1.3节中，多元高斯分布的公式 可知 信息矩阵 为：
参考：
深蓝 VIO课程
多元高斯分布_均值和方差为0的高斯分布_aliphantom的博客-CSDN博客
期望E与高斯分布的期望_高斯分布的期望和方差_惊鸿一博的博客-CSDN博客
二维随机向量的数学期望E与协方差σ_惊鸿一博的博客-CSDN博客
