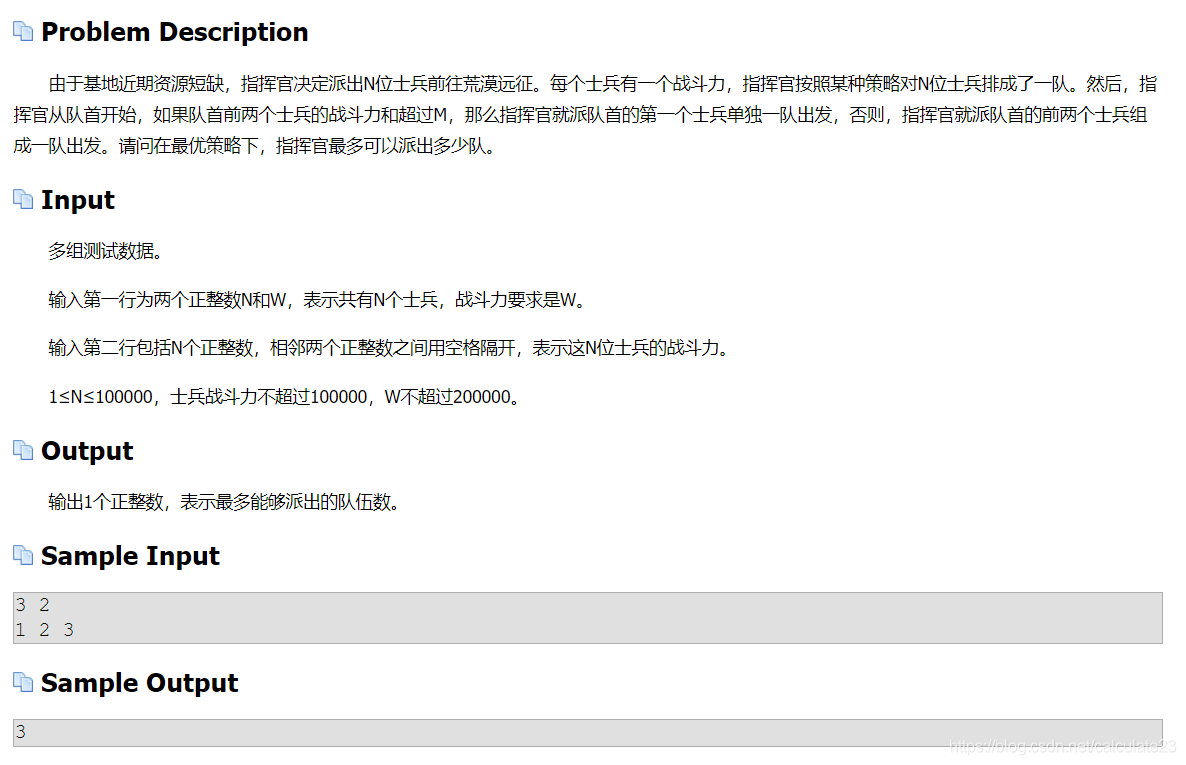
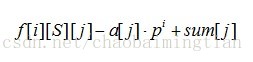题目链接：https://www.dotcpp.com/oj/problem2306.html 

这里说明一下后缀表达式(做这个题之前，我不太理解后缀表达式)。

后缀表达式，又称逆波兰式，指的是不包含括号，运算符放在两个运算对象的后面，所有的计算按运算符出现的顺序，严格从左向右进行（不再考虑运算符的优先规则）。

 

后缀表达式计算：
后缀表达式计算与前缀表达式类似，只是顺序是从左至右，具体过程如下：
从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 op 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果

例如：后缀表达式为“2 3 + 4 × 5 -”计算过程如下：
  （1）从左至右扫描，将 2 和 3 压入堆栈；
  （2）遇到 + 运算符，因此弹出 3 和 2（ 3 为栈顶元素，2 为次顶元素，注意与前缀表达式做比较），计算出 3+2 的值，得 5，再将 5 入栈；
  （3）将 4 入栈；
  （4）接下来是 × 运算符，因此弹出 4 和 5，计算出 4 × 5 = 20，将 20 入栈；
  （5）将 5 入栈；
  （6）最后是-运算符，计算出 20-5 的值，即 15，由此得出最终结果。

 

中缀表达式转后缀表达式：
与转换为前缀表达式相似，步骤如下：
  （1）初始化两个栈：运算符栈s1和储存中间结果的栈s2；
  （2）从左至右扫描中缀表达式；
  （3）遇到操作数时，将其压s2；
  （4）遇到运算符时，比较其与 s1 栈顶运算符的优先级：
    a：如果 s1 为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
    b：否则，若优先级比栈顶运算符的高，也将运算符压入 s1（注意转换为前缀表达式时是优先级较高或相同，而这里则不包括相同的情况）;
    c：否则，将 s1 栈顶的运算符弹出并压入到 s2 中，再次转到（4）-（1）与s1中新的栈顶运算符相比较；
  （5）遇到括号时：
    a：如果是左括号“(”，则直接压入 s1；
    b：如果是右括号“)”，则依次弹出 s1 栈顶的运算符，并压入 s2 ，直到遇到左括号为止，此时将这一对括号丢弃；
  （6）重复步骤（2）至（5），直到表达式的最右边；
  （7）将 s1 中剩余的运算符依次弹出并压入 s2；
  （8）依次弹出 s2 中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式（转换为前缀表达式时不用逆序）

例如，将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程如下：

扫描到的元素	s2(栈底->栈顶)	s1 (栈底->栈顶)	说明
1	1	空	数字，直接入栈
+	1	+	s1为空，运算符直接入栈
(	1	+ (	左括号，直接入栈
(	1	+ ( (	同上
2	1 2	+ ( (	数字
+	1 2	+ ( ( +	s1栈顶为左括号，运算符直接入栈
3	1 2 3	+ ( ( +	数字
)	1 2 3 +	+ (	右括号，弹出运算符直至遇到左括号
×	1 2 3 +	+ ( ×	s1栈顶为左括号，运算符直接入栈
4	1 2 3 + 4	+ ( ×	数字
)	1 2 3 + 4 ×	+	右括号，弹出运算符直至遇到左括号
-	1 2 3 + 4 × +	-	-与+优先级相同，因此弹出+，再压入-
5	1 2 3 + 4 × + 5	-	数字
到达最右端	1 2 3 + 4 × + 5 -	空	s1中剩余的运算符

得到的最终结果为：“ 1 2 3 + 4 × + 5 - ”

题目描述

给定 N 个加号、M 个减号以及 N + M + 1 个整数 A1, A2, · · · , AN+M+1，小 明想知道在所有由这 N 个加号、M 个减号以及 N + M + 1 个整数凑出的合法的 后缀表达式中，结果最大的是哪一个?

请你输出这个最大的结果。
例如使用1 2 3 + -，则 “2 3 + 1 -” 这个后缀表达式结果是 4，是最大的。

输入

第一行包含两个整数 N 和 M。
第二行包含 N + M + 1 个整数 A1, A2, · · · , AN+M+1。

输出

输出一个数，表示答案

样例输入

1 1
1 2 3

样例输出

4

提示

对于所有评测用例，0 ≤ N, M ≤ 100000，−109 ≤ Ai

 

题目思路：只要理解了后缀表达式如何计算，就简单了。

讨论：len表示数的个数，n表示+的数目，m表示-的数目，ans表示负数的个数

这个题目需要考虑的是负号的使用，会使负数转为正数。

1. m==0时，所有的数之和就是最后的结果，因为无负号。

2.ans==0时，最大值为 最大的len-1个非负数之和减去最小的非负数。

例如:5 4 3 2 1,n=2,m=2;  此时 5+4+3-(1-2)=5+4+3+2-1

3.ans!=0时。

①ans!=len时。最大值为所有数的绝对值之和。

例如：5 4 -3 -2 -1，n=2,m=2; 此时 5+4-((-3)+(-2))-(-1)=5+4+3+2+1

5 4 3 -2 -1, n=1,m=3; 此时 5+4-((-2)-3)-(-1)=5+4+3+2+1

②ans==len时。此时全为负数。最大值为 绝对值最大的len-1个数的绝对值之和减去绝对值最小的数的绝对值。

AC代码： 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<vector>
#include<string>
#define cla(a, sum) memset(a, sum, sizeof(a))
#define rap(i,m,n) for(i=m;i<=n;i++)
#define rep(i,m,n) for(i=m;i>=n;i--)
#define PI acos(-1)
using namespace std;
typedef long long ll;
typedef pair<ll,ll>P;
const int Inf=0x3f3f3f3f;
const double eps=1e-6;
const int maxn=2e5+5;ll n,m;
ll a[maxn],sum;
ll ans,len;int main()
{cin>>n>>m;ll i,j,k;sum=0;ans=0;len=n+m+1;rap(i,1,len){scanf("%lld",&a[i]);sum+=a[i];if(a[i]<0)ans++;}if(m==0){cout<<sum<<endl;return 0;} sort(a+1,a+len+1);if(!ans){sum-=2*a[1];}else{if(ans==len){//全为负数 rap(i,1,ans-1)sum-=2*a[i]; }else rap(i,1,ans)sum-=2*a[i];}cout<<sum<<endl;return 0;
}