本文来自公众号“AI大道理”
Network Slimming剪枝是比较广泛的一种模型剪枝方法,作者来自清华大学、英特尔中国实验室、复旦大学和科内尔大学。

1、Network Slimming剪枝理论
Network Slimming剪枝是结构性剪枝,是通道剪枝,是静态剪枝。
Network Slimming利用了BN层中的缩放因子γ来控制通道的重要性。
BN层:
BN层是归一化操作,将数据归一化到均值为0,方差为1上,防止数值逐步变大,不利于神经网络的训练。
通常插入在卷积和全连接之后,在非线性处理前。
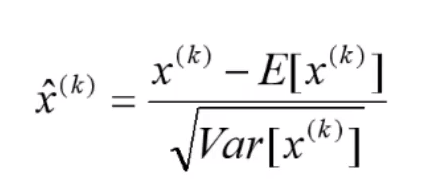
若都是线性的,神经网络将失去意义。
因此,需要在BN后再次进行变换,以提供一定的非线性。
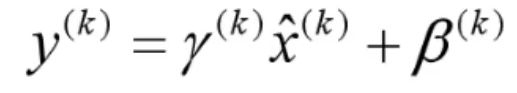
BN引入了两个可训练的参数γ和β。
随着𝛾更新, 约束项会将𝛾拉向0,从而判断这个通道不重要,进行剪枝。
(灵魂的拷问:γ参数控制着谁的通道?通道剪枝是剪枝谁的通道?是特征图的通道,还是卷积核的通道?)
答:先卷积,再BN,是对特征图里面的数据进行求均值,方差。
γZ依然在控制特征图的数据,根据γ判断通道重要性,是控制特征图的通道。
是对特征图的通道进行剪枝。
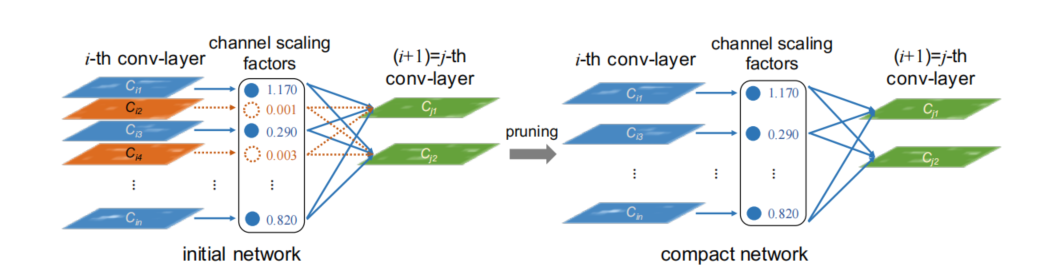
将缩放因子(参数γ)与卷积层中的每个通道相关联。
在训练期间对这些缩放因子施加稀疏正则化,以自动识别不重要的通道。
具有较小缩放因子值的通道将被剪枝。
剪枝后,获得紧凑模型,然后对其进行微调以达到与正常训练的网络相当(甚至更高)的精度。
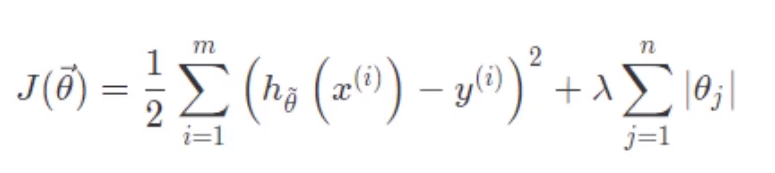
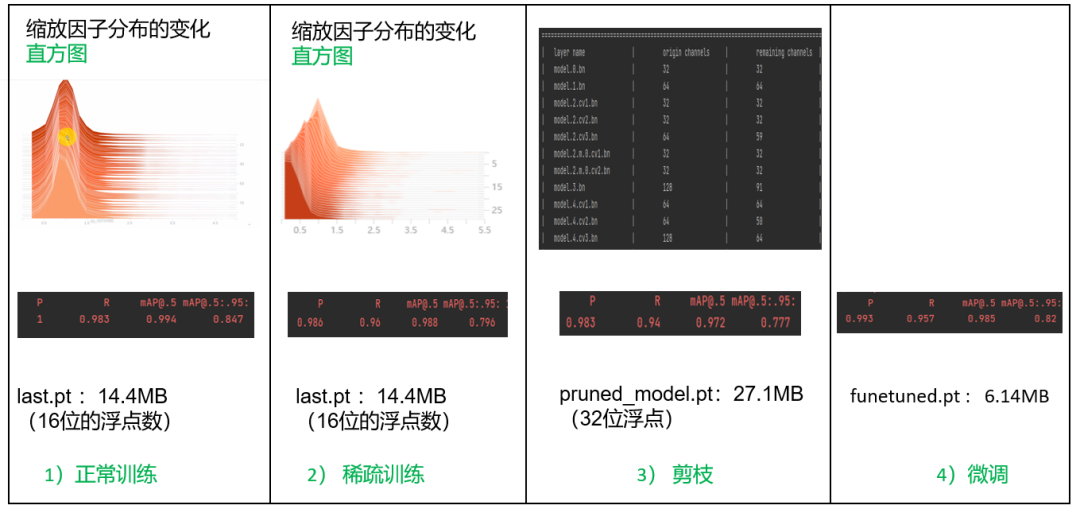
稀疏训练后,剪掉一个BN层,需要将对应上一层的卷积核裁剪掉,同时将BN层后下一层卷积核对应的通道减掉。
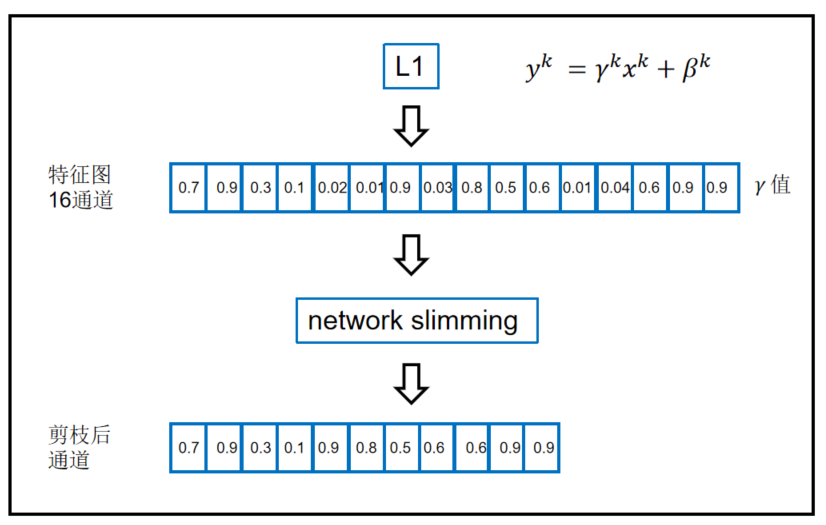
γ越小,对应的通道越不重要。
(灵魂的拷问:L1为什么能达到稀疏正则化的效果?)
L1正则化:
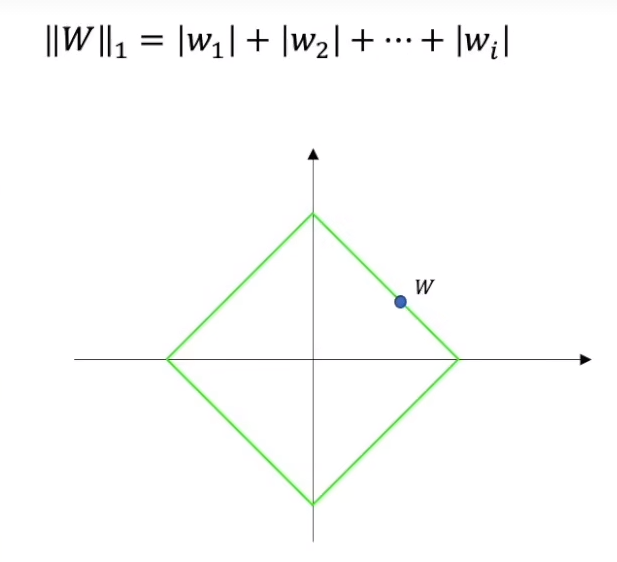
L1范数:
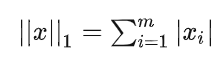
即向量元素绝对值之和,x 到零点的曼哈顿距离。
L1范数就是所有元素绝对值的和。
把L1范数相同的点组和在一起就是一个正方形。
添加L1正则化的损失函数为:
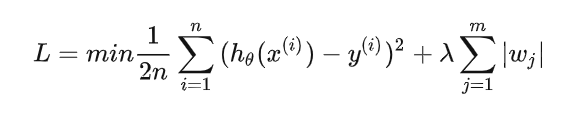
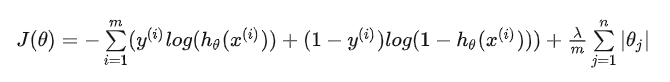
其中,后面这项就是L1范数,也就是原来损失函数的惩罚项。
所谓惩罚项,其实就是和原来的损失函数竞争,现在要满足两者的最小值才是真正的最小值。
其中,L1正则化项的损失函数是一个个正方形,而原来的损失函数是一个个椭圆,只有两者的交点才使得整体损失最小。
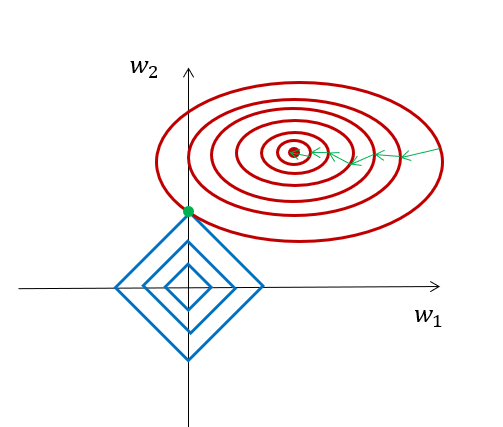
这样就会产生很多0值,达到稀疏化的效果。

2、模型剪枝流程
1)正常训练
从头开始训练网络作为基线。
2) 稀疏训练
使用L1稀疏正则化进行训练时,控制经验损失和稀疏性之间的折中的超参数 。
3) 剪枝
需要确定比例因子的修剪阈值。使用全局修剪阈值。修剪阈值由所有比例因子中的百分比来确定,例如,40%或 60%的通道被修剪。通过建立一个新的更窄的模型并从用稀疏度训练的模型中复制相应的权重来训练。
4)微调
修剪后,获得了一个更窄、更紧凑的模型,然后对其进行微调。

3、Network Slimming剪枝实战
为了加速运算,我们通常将BN层和卷积层融合起来。
现在为了能够控制通道的重要性,Network Slimming在训练的时候BN层不能融合起来训练,而应该拆开。
yolov5会通过model.fuse()将卷积层和bn层融合。
为了对bn层剪枝,训练和保存的时候先不要做融合。
剪枝实战:
1)正常训练
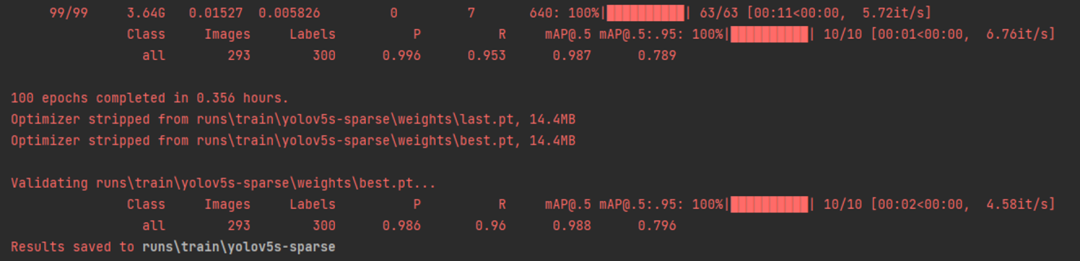
YOLOv5s的常规训练,训练100epoch作为基准。
缩放因子分布的变化:

训练结果与指标:

last.pt大小为14.4MB(16位的浮点数)。
2) 稀疏训练
YOLOv5s的稀疏训练,训练100epoch。
缩放因子分布的变化:

训练结果与指标:
last.pt :14.4MB(16位的浮点数)。
可以看到bn训练中缩放因子分布的变化,随着训练(纵轴从上往下)进行,直方图逼近0附近,说明大多数bn已经变得稀疏。
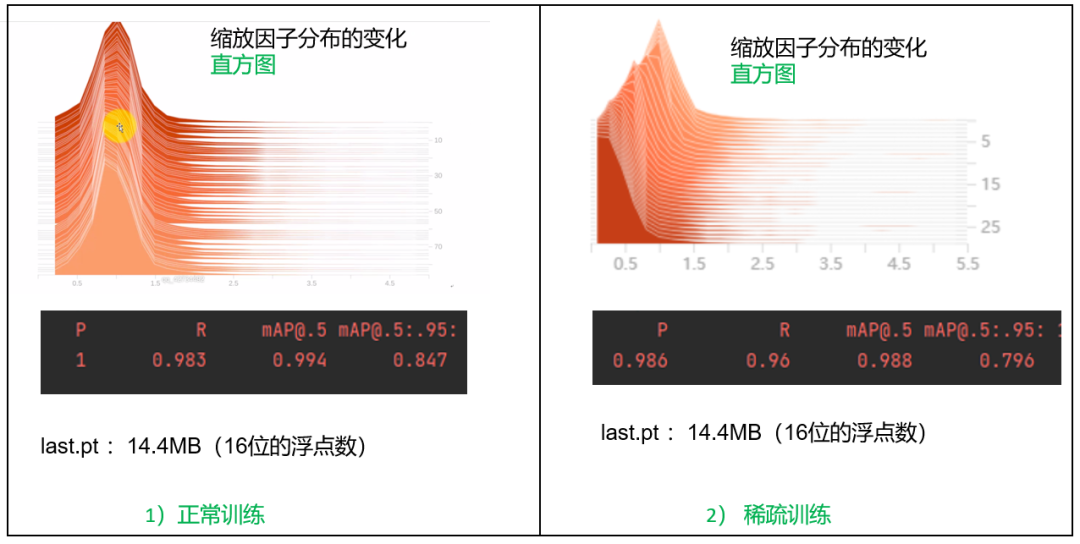
稀疏训练之后模型指标在下降。
3) 剪枝
剪枝率0.5。
剪枝后的网络情况:
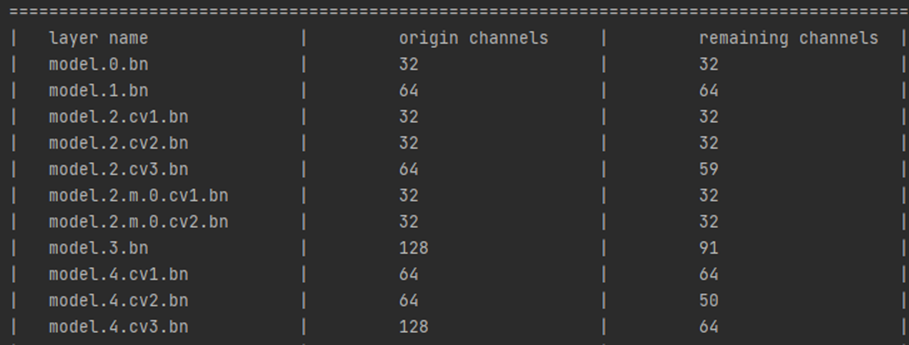
可见通道数的确在变少。
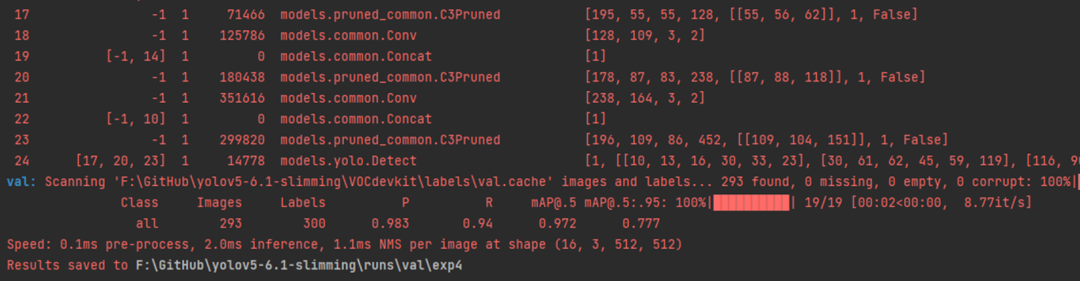
剪枝后会生成pruned_model.pt模型,大小27.1MB(32位浮点)
original_model.pt->pruned_model.pt(32位浮点)
4)微调
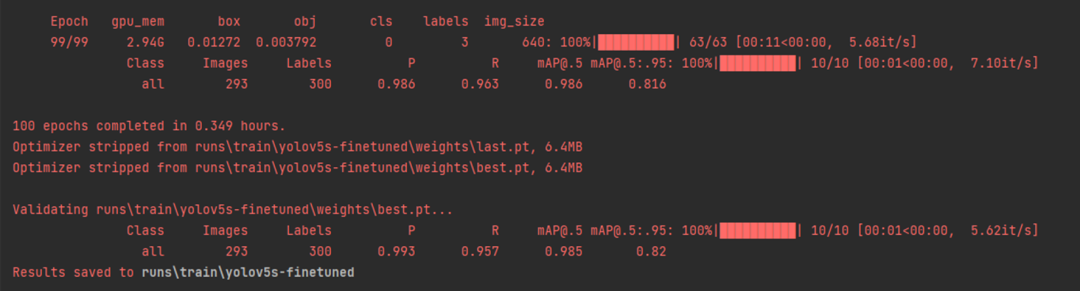
funetuned.pt : 6.14MB(16位的浮点数)
可见经过微调后,精度和召回率等指标又上升了一点,逼近未剪枝之前的指标。

4、Network Slimming剪枝效果评估
网络变化:
通道变少。
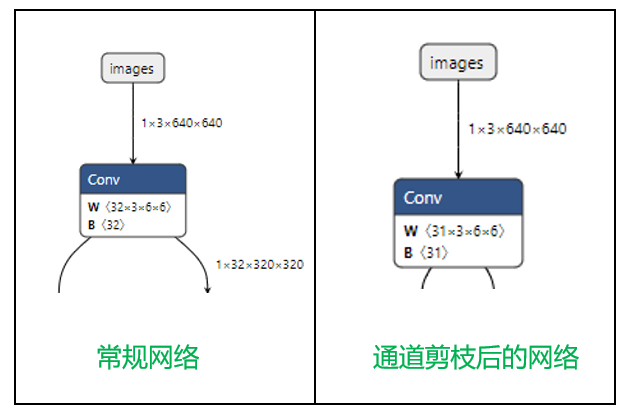
模型大小变化:
减小了57.4%

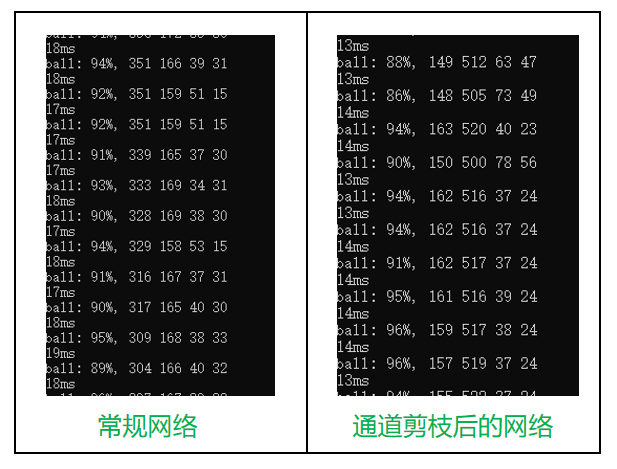
速度变化:
变快了27.8%

5、总结
Network Slimming剪枝是结构性剪枝,是通道剪枝,是静态剪枝。
Network Slimming利用了BN层中的缩放因子γ来控制通道的重要性。
Network Slimming剪枝后模型通道变少,模型大小变小,推理速度变快。

——————
浅谈则止,细致入微AI大道理
扫描下方“AI大道理”,选择“关注”公众号
—————————————————————
—————————————————————
投稿吧 | 留言吧