噪声分类

热噪声(Thermal Noise)：最基本的一种噪声，就像冬日里北方的霾一样，可以说是无处不在的。热噪声又称为Johanson或Nyquist噪声，是由电子的热运动产生的。在绝对零度(0 K)以上，就会存在自由电子的热运动。因此，几乎所有的器件/设备，都会产生热噪声。热噪声的功率谱密度不随频率变化，称为白噪声，又因服从Gauss概率密度分布，所以又称为高斯白噪声。
散粒噪声(Shot Noise)：由电子管或半导体固态设备中载流子的随机波动产生的，比如PN结二极管，当级间存在电压差时，就会发生电子和空穴的移动，此过程中就会产生散粒噪声。其功率谱密度也不随频率变化，也是一种白噪声。散粒噪声是半导体器件所特有的，无源器件(比如衰减器)是不产生散粒噪声的。
闪烁噪声(Flicker Noise)：产生于真空管(阴极氧化涂层)或半导体(半导体晶体表面缺陷)固态设备。噪声功率主要集中在低频段，其功率谱密度与频率成反比，所以又称为1/f 噪声。高于一定频率时，其噪声功率谱非常微弱，但是平坦的。因此，有时也称为pink noise.
等离子体噪声(Plasma Noise)：因电离化气体中电荷的随机运动产生，如电离层中或电火花接触时，就会产生等离子体噪声。
量子噪声(Quantum Noise)：因载流子或光子的量子化特性所产生。
对于电子器件而言，相对其它三种噪声，最后两种噪声是可以忽略的。

噪声系数的定义

电阻(无源器件)的输出噪声功率

将一个电阻置于温度为T (开尔文温度)的环境中，电阻中的自由电子随机运动，动能与温度T成正比。电子的随机运动会产生小的随机电压波动，此时电阻相当于一个噪声源，输出波形如图1所示，该噪声在足够长时间内的算术平均值为0，但RMS平均值值不为零。
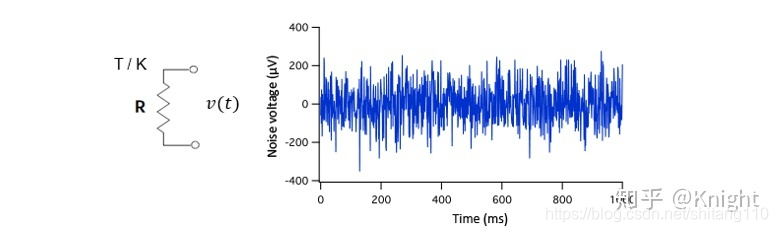在这里插入图片描述图1. 电阻产生的随机噪声
噪声电压的有效值可以简化为： $V_{n} =\sqrt{4kTBR}$
上式可以看出，噪声电压有效值与频率无关，且为常数，是一种白噪声。

可将电阻等效为一个内阻为R的噪声源，当构成图2所示的共轭匹配电路时，其可输出最大噪声功率为:
$P_{n,max} =(\frac{V_{n} }{2R} )^2R=KTB$
在这里插入图片描述
由上式可知，电阻输出的最大噪声功率只与当前温度及系统带宽有关，与电阻值无关。
对于衰减器等无源器件而言，因其内部只有电子热运动，只产生热噪声，所以情况与电阻类似。

半导体器件

基于半导体的器件，虽然产生的噪声种类相对多一些，但是可以将所有的噪声等效为热噪声，其输出最大噪声功率的能力，使用等效噪声温度Te表征。
在这里插入图片描述图3. 将有源器件等效为热噪声源
共轭匹配时，器件输出的最大噪声功率为： $N_{o} =KT_{e}B$
式中， $T_{e}$ 为器件的等效噪声温度。

放大器

对于放大器，等效噪声电路如图4所示，放大器本身可以产生噪声，为了引入等效噪声温度，假设输入端连接了一个电阻R，但是在绝对温度0K时，该电阻并不产生噪声功率，放大器的输出噪声功率只源自于自身。等效之后，放大器只有增益G而不会产生噪声功率，而输入端提供一个 $KT_{e}B$ 的等效噪声输入功率，此时放大器输出噪声功率为： $N_{o} =KT_{e}BG$
在这里插入图片描述
图4. 放大器的等效噪声电路

噪声因子

IEEE给出的噪声因子定义为：在290K温度下，器件输出的总噪声功率与仅仅输入噪声功率引起的输出噪声功率的比值。
通常情况下，工程师们更习惯于朗朗上口的定义：噪声因子为器件或系统的输入与输出信噪比之比。很显然，噪声因子表征了信号经过器件后信噪比的恶化程度。
$F=\frac{S_{i} /N_{i} }{S_{o} /N_{o} } =\frac{N_{i} \cdot G+N_{a} }{N_{i} \cdot G}$
式中 $N_{i}$ 为290K温度下对应的噪声输入功率， $N_{o}$ 为总输出噪声功率， $N_{a}$ 为器件本身引入的输出噪声功率， $G$ 为器件增益。
在这里插入图片描述
图5. 放大器的等效噪声电路
IEEE对噪声因子的定义基于两个条件：290K开尔文温度下，且端口阻抗匹配。通常所说的噪声因子或噪声系数都是在这两个条件下定义的。后续篇章涉及到的数学公式推导及噪声系数的测试都是基于这两个条件。
在 $T_{0}$ =290K温度下，放大器的输入噪声功率为 $KBT_{0}$ ，假设其等效噪声温度为 $T_{e}$ ，则噪声因子F为:
$F=\frac{N_{i} \cdot G+N_{a} }{N_{i} \cdot G} =\frac{KBT_{0} G+KBT_{e} G}{KBT_{0} G}$
进一步化简得: $F=1+\frac{T_{e} }{T_{0} }$

噪声系数NF

$N F = 10 l g F$

无源器件的噪声系数

但凡从事RF/µW相关职业的工程师，对于无源器件的噪声系数都有一个共识：噪声系数与插入损耗相同。比如6dB的衰减器，其噪声系数就是6dB。其实这个共识也有一个非常重要的前提——290K（ $T_{0}$ ）温度下。
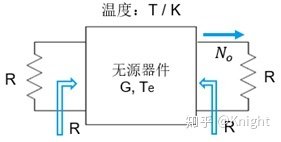
在这里插入图片描述
图6. 无源器件的等效噪声电路

图6给出了无源器件的等效噪声电路，假设输入、输出都是匹配的，当前温度为T，无源器件的增益和等效噪声温度分别为G和 $T_{e}$ （290K下计算出的值），因为整个系统处于热平衡状态，所以其输出的噪声功率为 $KBT_{}$ ，且满足如下关系式： $N_{o} =KBTG+KBT_{e} G=KBT$
化简得到: $T_{e} =(\frac{1}{G}-1 )\cdot T$
依据等效噪声温度与噪声因子的关系可以得到: $F=1+\frac{T_{e} }{T_{0} }=1+(\frac{1}{G}-1 )\cdot \frac{T}{T_{0}}$
当 $T=T_{0}$ 时，上式可化简为: $F=\frac{1}{G}$ $NF=10lg(\frac{1}{G})=-10lg(G)$
也就是说，只有在T0=290K温度下，无源器件的噪声系数才等于其插入损耗。

值得一提的是，无源混频器的噪声系数并不等于变频损耗，因为除了产生热噪声外，还会产生散粒噪声和闪烁噪声，不满足上面提到的热平衡状态，只有仅仅产生热噪声的器件才会达到热平衡态。

噪声系数的级联

在这里插入图片描述
图7. 两级器件级联及噪声输出示意图
图7给出了两级放大器级联示意图，级联后输出的总噪声功率为： $N_{o} =KTBG_{1} G_{2} +N_{a1} G_{2} +N_{a2} =KTBG_{1} G_{2} +KT_{e1} BG_{1} G_{2} +KBT_{e2} G_{2}$ 式中，Te1、Te2分别为两个放大器的等效噪声温度。当然，处于同一个链路中，也认为两个器件的带宽B是相同的。

如果将两个级联DUT的总等效噪声温度设为Te，则总输出噪声功率为: $N_{o} =KTBG_{1} G_{2} +KT_{e} BG_{1} G_{2}$ 从而得到两级联后的总等效噪声温度和噪声因子: $T_{e}=T_{e1}+\frac{T_{e2}}{G_{1}} \Rightarrow F=F_{1} +\frac{F_{2} -1}{G_{1} }$ 以此类推，对于N级器件级联后，则满足如下关系: $T_{e}=T_{e1}+\frac{T_{e2}}{G_{1} } +\cdots +\frac{T_{eN}}{G_{1}G_{2}\cdots G_{N} }$ $F=F_{1} +\frac{F_{2} -1}{G_{1} } +\cdots +\frac{F_{N} -1}{G_{1}G_{2}\cdots G_{N} }$ 公式表明，第一级器件的选择对于整个链路的NF有比较大的影响，这也是为什么在接收机链路中第一级采用LNA的原因。

噪声系数对系统的影响

绝大多数情况下，器件或系统产生的噪声都是有害的，当然也有例外，比如噪声源就是专门产生宽带噪声的设备，用于NF测试，或者验证系统的抗噪声性能。

在绝对零度以上，任何器件均会产生噪声，那么当信号经过器件时，必然会导致信噪比SNR的降低，就好比一张清晰的图片，引入噪声后却变得模糊。
在这里插入图片描述图8. 噪声系数导致SNR恶化

射频收发链路中，通常接收机链路更加关注噪声系数，因为这决定了接收机的灵敏度，噪声系数越低，接收灵敏度越高，二者存在如下关系。
在这里插入图片描述
从应用的角度讲，接收机噪声系数对雷达和通信系统性能至关重要。较高的噪声系数直接限制了雷达最远探测距离，类似地，对于目前广泛应用的宽带通信系统，往往采用高阶、复杂的数字调制，这类调制信号对于SNR要求更高，如果接收机灵敏度不够高，会导致误码的产生，从而影响数据的有效传输。
在这里插入图片描述