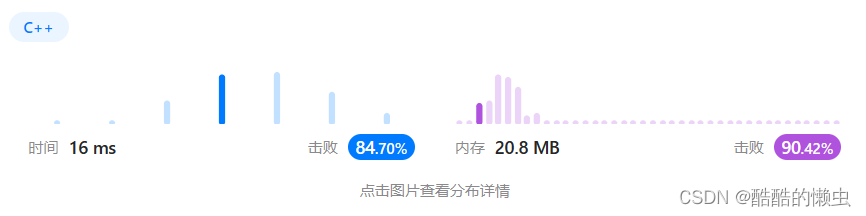
修改图中的边权【LC2699】

给你一个 n 个节点的 无向带权连通 图，节点编号为 0 到 n - 1 ，再给你一个整数数组 edges ，其中 edges[i] = [ai, bi, wi] 表示节点 ai 和 bi 之间有一条边权为 wi 的边。

部分边的边权为 -1（wi = -1），其他边的边权都为 正 数（wi > 0）。

你需要将所有边权为 -1 的边都修改为范围 [1, 2 * 109] 中的 正整数 ，使得从节点 source 到节点 destination 的 最短距离 为整数 target 。如果有 多种 修改方案可以使 source 和 destination 之间的最短距离等于 target ，你可以返回任意一种方案。

如果存在使 source 到 destination 最短距离为 target 的方案，请你按任意顺序返回包含所有边的数组（包括未修改边权的边）。如果不存在这样的方案，请你返回一个 空数组 。

**注意：**你不能修改一开始边权为正数的边。

这两天为啥那么难

• 思路

  • 首先题意要求最短路径为target，如果$\lceil$不包含-1的边时最短距离小于target$\rfloor$或者$\lceil$当所有-1的边修改为1时最短距离大于target$\rfloor$，那么此时无解

  • 通过两次Dijkstra 算法判断是否有合法路径存在，以及如果存在边值为多少

    设第一次/第二次Dijkstra 算法时起点至点$i$的距离分别为$d_{i,0},d_{i,1}$

    • 第一次：将所有-1边的值改为1，通过Dijkstra 算法找到起点至终点的最短距离，如果大于target，那么无解，直接返回空数组；否则进行第二次最短路径搜索。

    • 第二次：通过第一次的结果可知，我们可以增大某一条-1的边使最短路径增大至target，我们需要按照某一种顺序修改边值，并且修改后不会使之后的路径值更小，否则会影响最终的最短路径。那么可以再一次使用Dijkstra 算法，保证每次拿到的点的最短路就是最终的最短路。

      当遇到一条可以修改边值的边$x-y$时，假设修改后的值为$w$，那么我们需要达到的目标使路径$source-X-Y-destination$的路径值为target
      $$d_{x,0}+w+d_{destination,0}-d_{y,0}=target$$
      那么w为
      $$target-d_{x,0}-d_{destination,0}+d_{y,0}$$
      此时还存在一种情况：如果修改完所有的值，最短路径仍小于target，此时也返回空数组

• 实现

  • 由于最后需要更改数组中的权值，因此构建邻接数组时需要记录边的下标
  • 第二次Dijkstra 算法时，当修改不在最短路径上的边$X-Y$的权值时，不会对答案产生影响
  • 最后可能会有部分边权值为-1，因为第一次Dijkstra 算法时没有将数组中的值改为1，或者有些边不影响最短路，把这些边都改成 1 就行。

  class Solution {public int[][] modifiedGraphEdges(int n, int[][] edges, int source, int destination, int target) {List<int[]> g[] = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for (int i = 0; i < edges.length; i++) {int x = edges[i][0], y = edges[i][1];g[x].add(new int[]{y, i});g[y].add(new int[]{x, i}); // 建图，额外记录边的编号}var dis = new int[n][2];for (int i = 0; i < n; i++)if (i != source)dis[i][0] = dis[i][1] = Integer.MAX_VALUE;dijkstra(g, edges, destination, dis, 0, 0);int delta = target - dis[destination][0];if (delta < 0) // -1 全改为 1 时，最短路比 target 还大return new int[][]{};dijkstra(g, edges, destination, dis, delta, 1);if (dis[destination][1] < target) // 最短路无法再变大，无法达到 targetreturn new int[][]{};for (var e : edges)if (e[2] == -1) // 剩余没修改的边全部改成 1e[2] = 1;return edges;}// 朴素 Dijkstra 算法// 这里 k 表示第一次/第二次private void dijkstra(List<int[]> g[], int[][] edges, int destination, int[][] dis, int delta, int k) {int n = g.length;var vis = new boolean[n];for (; ; ) {// 找到当前最短路，去更新它的邻居的最短路// 根据数学归纳法，dis[x][k] 一定是最短路长度int x = -1;for (int i = 0; i < n; ++i)if (!vis[i] && (x < 0 || dis[i][k] < dis[x][k]))x = i;if (x == destination) // 起点 source 到终点 destination 的最短路已确定return;vis[x] = true; // 标记，在后续的循环中无需反复更新 x 到其余点的最短路长度for (var e : g[x]) {int y = e[0], eid = e[1];int wt = edges[eid][2];if (wt == -1)wt = 1; // -1 改成 1if (k == 1 && edges[eid][2] == -1) {// 第二次 Dijkstra，改成 wint w = delta + dis[y][0] - dis[x][1];if (w > wt)edges[eid][2] = wt = w; // 直接在 edges 上修改}// 更新最短路dis[y][k] = Math.min(dis[y][k], dis[x][k] + wt);}}}
  }作者：灵茶山艾府
  链接：https://leetcode.cn/problems/modify-graph-edge-weights/solutions/2278296/xiang-xi-fen-xi-liang-ci-dijkstrachou-mi-gv1m/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
  

  • 复杂度
    • 时间复杂度：$\mathcal{O}(n^2)$，在稠密图（本题最坏情况）中，算法的时间复杂度与边的数量 $\mathcal{O}(n^2)$成正比。
    • 空间复杂度：$\mathcal{O}(m)$