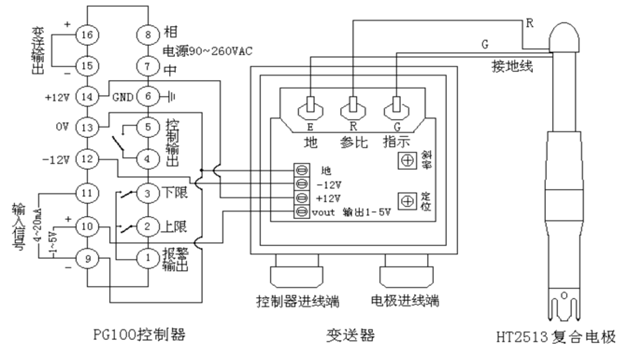
无源RC滤波器“滤除”不需要的信号,因为它们分离并允许仅通过其频率的正弦输入信号,最简单的是无源低通滤波器网络。
在低频应用(高达100kHz)中,无源滤波器通常使用简单的RC(电阻-电容)网络构建,而高频滤波器(高于100kHz)通常由RLC(电阻-电感-电容)元件制成。
无源滤波器由电阻器、电容器和电感器等无源元件组成,没有放大元件(晶体管、运算放大器等),因此没有信号增益,因此它们的输出电平始终小于输入。
滤波器是根据它们允许通过它们的信号的频率范围来命名的,同时阻挡或“衰减”其余部分。最常用的滤波器设计是:
- 低通滤波器 – 低通滤波器仅允许从 0Hz 到其截止频率 ƒc 点的低频信号通过,同时阻断任何更高的信号。
- 高通滤波器 – 高通滤波器仅允许来自其截止频率ƒc点和更高到无穷大的高频信号通过,同时阻挡那些更低的信号。
- 带通滤波器 – 带通滤波器允许落在两点之间的特定频带设置内的信号通过,同时阻挡该频段两侧的较低和较高频率。
简单的一阶无源滤波器(一阶)可以通过在输入信号(Vin) 与滤波器的输出, ( Vout)取自这两个分量的交界处。
根据我们连接电阻的方式,电容器相对于输出信号决定了滤波器结构的类型,从而产生低通滤波器或高通滤波器。
由于任何滤波器的功能都是允许给定频率带的信号不改变地通过,同时衰减或减弱所有其他不需要的信号,因此我们可以通过使用四种基本滤波器类型的理想频率响应曲线来定义理想滤波器的幅度响应特性,如图所示。
理想滤波器响应曲线

滤波器可分为两种不同的类型:有源滤波器和无源滤波器。有源滤波器包含放大装置以增加信号强度,而无源滤波器不包含放大装置以增强信号。由于无源滤波器设计中有两个无源元件,输出信号的幅度小于其相应的输入信号,因此无源RC滤波器衰减信号并且增益小于1(单位)。
低通滤波器可以是电容、电感或电阻的组合,旨在产生高于指定频率的高衰减,而低于该频率的衰减很小或没有衰减。发生转换的频率称为“截止”或“转角”频率。
最简单的低通滤波器由电阻和电容器组成,但更复杂的低通滤波器具有串联电感器和并联电容器的组合。在本教程中,我们将介绍最简单的类型,即无源双分量RC低通滤波器。
低通滤波器
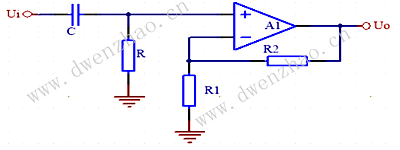
一个简单的无源RC低通滤波器或LPF可以很容易地通过串联单个电阻器和单个电容器来制造,如下所示。在这种类型的滤波器布置中,输入信号( Vin) 应用于串联组合(电阻器和电容器一起),但输出信号 ( Vout) 仅在电容器上取。
这种类型的滤波器通常被称为“一阶滤波器”或“单极点滤波器”,为什么是一阶或单极点?,因为它在电路中只有“一个”无功分量,即电容器。

如前面的容性电抗教程所述,电容器的电抗随频率变化相反,而电阻的值随频率变化而保持恒定。在低频下,容性电抗(XC)的电容器将与电阻的电阻值R相比非常大。
这意味着电压电位,VC两端的电容会比电压降大得多,VR在电阻器两端展开。在高频下,V则相反C小而VR由于容抗值的变化而变大。
虽然上面的电路是RC低通滤波器电路,但它也可以被认为是一个频率相关的可变电位分压器电路,类似于我们在电阻教程。在该教程中,我们使用以下等式来计算串联连接的两个单个电阻器的输出电压。

我们还知道,交流电路中电容器的容抗给出如下:

交流电路中电流的对冲称为阻抗,符号Z,对于由单个电阻器与单个电容器串联组成的串联电路,电路阻抗计算公式为:

后,通过将上面的阻抗方程代入电阻电位分压器方程,得到:
RC 电位分配器方程

因此,通过使用两个串联电阻的电位分压方程并代入阻抗,我们可以计算出任何给定频率下RC滤波器的输出电压。
低通滤波器示例1
一个由一个 4k7Ω 电阻器与一个 47nF 电容器串联而成的低通滤波器电路连接在一个 10v 正弦电源上。计算输出电压 (V外) 的频率为 100Hz,频率为 10,000Hz 或 10kHz。
频率为 100Hz 时的电压输出。

频率响应
从上面的结果中我们可以看出,当施加到RC网络的频率从100Hz增加到10kHz时,电容器上的电压下降,因此输出电压(V外)从电路从9.9v降低到0.718v。
通过将网络输出电压与不同的输入频率值进行绘制,可以找到低通滤波器电路的频率响应曲线或波特图函数,如下所示。
一阶低通滤波器的频率响应

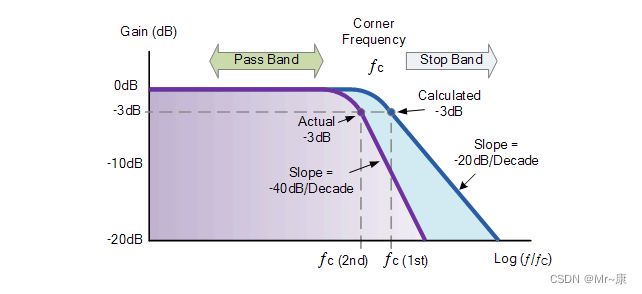
波特图显示滤波器的频率响应在低频时几乎是平坦的,并且所有输入信号都直接传递到输出,导致增益接近1,称为单位,直到达到其截止频率点(ƒc)。这是因为电容器的电抗在低频时很高,并阻挡了流过电容器的任何电流。
在此截止频率点之后,电路的响应在-20dB/十倍或(-6dB/倍频程)的斜率下降至零。请注意,斜率的角度,对于任何RC组合,这个-20dB /十年滚降将始终相同。
施加到该截止频率点以上的低通滤波电路上的任何高频信号都会变得非常衰减,即它们迅速下降。发生这种情况是因为在非常高的频率下,电容器的电抗变得如此之低,以至于它对输出端子产生短路条件的影响,从而导致零输出。
然后,通过仔细选择正确的电阻-电容组合,我们可以创建一个RC电路,允许低于特定值的频率范围不受影响地通过电路,同时施加到高于该截止点的电路的任何频率被衰减,从而产生通常称为低通滤波器。
对于这种类型的“低通滤波器”电路,低于此截止点ƒc的所有频率均未改变,几乎没有衰减,并且据说位于滤波器通带区。此通带区还表示滤波器的带宽。任何高于该截止点的信号频率一般都说是在滤波器阻带区,它们会被大大衰减。
该“截止”、“转角”或“断点”频率定义为容抗和电阻相等的频率点,R = Xc = 4k7Ω。发生这种情况时,输出信号衰减至输入信号值的70.7%或输入的-3dB(20对数(Vout/Vin))。虽然R = Xc,但输出不是输入信号的一半。这是因为它等于两者的向量和,因此是输入的0.707。
由于滤波器包含一个电容器,输出信号的相位角(Φ)落后于输入信号,在-3dB截止频率(ƒc)处为-45o异相。这是由于随着输入电压的变化,对电容器的板充电所花费的时间,导致输出电压(电容器两端的电压)“滞后”于输入信号的电压。施加到滤波器的输入频率越高,电容器滞后越多,电路变得越来越“异相”。
截止频率点和相移角可以通过以下公式找到:
截止频率和相移

然后,对于上面的“低通滤波器”电路的简单示例,截止频率(ƒc)给出为720Hz,输出电压为输入电压值的70.7%,相移角为-45°。
二阶低通滤波器
到目前为止,我们已经看到,简单的一阶RC低通滤波器可以通过将单个电阻器与单个电容器串联来制造。这种单极点排列使我们在截止点以上的频率衰减的滚降斜率为-20dB/十倍ƒ-3分贝.然而,有时在滤波电路中,这种-20dB/十倍频程(-6dB/倍频程)的斜率角可能不足以消除不需要的信号,然后可以使用两级滤波,如图所示。

上述电路使用两个无源一阶低通滤波器连接或“级联”在一起,形成二阶或双极点滤波器网络。因此,我们可以看到,一阶低通滤波器只需向其添加一个额外的RC网络即可转换为二阶类型,我们添加的RC级越多,滤波器的阶数就越高。
如果将许多(n)个这样的RC级联在一起,则得到的RC滤波器电路将被称为“n千-订单”滚降斜率为“n x -20dB/十倍”的滤波器。
例如,二阶滤波器的斜率为-40dB/倍频程(-12dB/倍频程),四阶滤波器的斜率为-80dB/十倍频程(-24dB/倍频程),依此类推。这意味着,随着滤波器阶数的增加,滚降斜率变得更陡峭,滤波器的实际阻带响应接近其理想的阻带特性。
二阶滤波器非常重要,广泛用于滤波器设计,因为当与一阶滤波器结合使用时,任何高阶n千-值过滤器可以使用它们进行设计。例如,三阶低通滤波器是通过串联或级联一个一阶和二阶低通滤波器而形成的。
但是,RC滤波器级联在一起也有一个缺点。虽然可以形成的滤波器的顺序没有限制,但随着阶次的增加,最终滤波器的增益和精度会下降。
当相同的RC滤波器级联在一起时,随着滚降斜率的增加,所需截止频率(ƒc)处的输出增益会降低(衰减)一个量。我们可以使用以下公式定义所选截止频率下的衰减量。
ƒc 时的无源低通滤波器增益

其中“n”是滤波器级的数目。
因此,对于二阶无源低通滤波器,拐角频率ƒc处的增益将等于0.7071 x 0.7071 = 0.5Vin (-6dB),三阶无源低通滤波器将等于0.353Vin (-9dB),四阶将等于0.25Vin (-12dB)依此类推。二阶无源低通滤波器的转折频率ƒc由电阻/电容(RC)组合决定,并给出为。
二阶滤波器转折频率

二阶低通滤波器 -3dB 频率

其中 ƒc 是计算的截止频率,n 是滤波器阶数,并且ƒ-3分贝是新的-3dB通带频率,由于滤波器阶数的增加。
然后,假设相同的-3dB截止点,二阶低通滤波器的频率响应(波特图)如下所示:
二阶低通滤波器的频率响应
在实践中,将无源滤波器级联在一起以产生大阶滤波器很难准确实现,因为每个滤波器阶的动态阻抗会影响其相邻网络。但是,为了降低负载效应,我们可以使每个后续阶段的阻抗是前一阶段的10倍,因此R2 = 10 x R1和C2 = 1/10th C1。二阶及以上滤波器网络通常用于运算放大器的反馈电路中,在RC振荡器电路中称为有源滤波器或相移网络。
低通滤波器摘要
总而言之,低通滤波器具有从DC(0Hz)到指定截止频率的恒定输出电压,ƒC) 点。该截止频率点为 0.707 或 -3dB ( dB = –20log*V出/入) 允许通过的电压增益。
频率范围“低于”此截止点ƒC通常被称为通带,因为输入信号允许通过滤波器。“高于”该截止点的频率范围通常被称为阻带,因为输入信号被阻挡或停止通过。
可以使用单个电阻器与输入信号 Vin 上的单个非极化电容器(或任何单个无功分量)串联来制作简单的一阶低通滤波器,而输出信号 Vout 则从电容器两端获取。
截止频率或-3dB点可以使用标准公式ƒc = 1/(2πRC)找到。输出信号在 ƒc 处的相位角为-45o用于低通滤波器。
滤波器或任何滤波器的增益通常以分贝表示,是输出值除以其相应输入值的函数,并给出为:

无源低通滤波器的应用是音频放大器和扬声器系统,用于将较低频率的低音信号定向到较大的低音扬声器,或减少任何高频噪声或“嘶嘶声”型失真。在音频应用中这样使用时,低通滤波器有时被称为“高切”或“高音切”滤波器。
如果我们要反转电阻和电容器在电路中的位置,以便输出电压现在从电阻两端获取,我们将得到一个电路,该电路产生类似于高通滤波器的输出频率响应曲线,这将在下一个教程中讨论。
时间常数
到目前为止,我们一直对低通滤波器在受到正弦波形时的频率响应感兴趣。我们还看到,滤波器截止频率(ƒc)是电路中电阻(R)和电容(C)相对于某个指定频率点的乘积,并且通过改变两个组件中的任何一个来改变这个截止频率点,要么增加它,要么减少它。
我们还知道,电路的相移滞后于输入信号的相移,因为随着正弦波的变化,对电容器充电然后放电所需的时间。这种R和C的组合对电容器产生充电和放电效应,称为电路的时间常数(τ),如RC电路教程所示,使滤波器在时域中响应。
时间常数 tau (τ) 与截止频率 ƒc 的关系为:

或用截止频率表示,ƒc表示为:

输出电压,V外取决于时间常数和输入信号的频率。正弦信号随时间平滑变化,电路表现为简单的一阶低通滤波器,如上图所示。
但是,如果我们将输入信号更改为具有几乎垂直步进输入的“方波”形状的“ON/OFF”型信号,那么我们的滤波电路现在会发生什么。电路的输出响应将发生巨大变化,并产生另一种类型的电路,通常称为积分器。
RC 集成商
积分器基本上是一个在时域中工作的低通滤波电路,当电容器充电和放电时,它将方波“阶跃”响应输入信号转换为三角形波形输出。三角形波形由交替但相等的正斜率和负斜率组成。
如下图所示,如果RC时间常数与输入波形的时间段相比较长,则得到的输出波形将是三角形的,输入频率越高,与输入频率相比,输出幅度就越低。
RC 积分器电路

这使得这种类型的电路非常适合将一种类型的电子信号转换为另一种类型的电子信号,以用于波产生或波形整形电路。