一、说明

其实实现凸包问题至少有五个方法，这里只介绍Graham-Scan经典算法。本文就该算法用代码实现，为了增加有趣性，我们用python实现。

二、算法描述

2.1 假设问题

假如您在楼下的A处，在G处有个电话亭，问您从哪个路径到达电话亭路程最短？

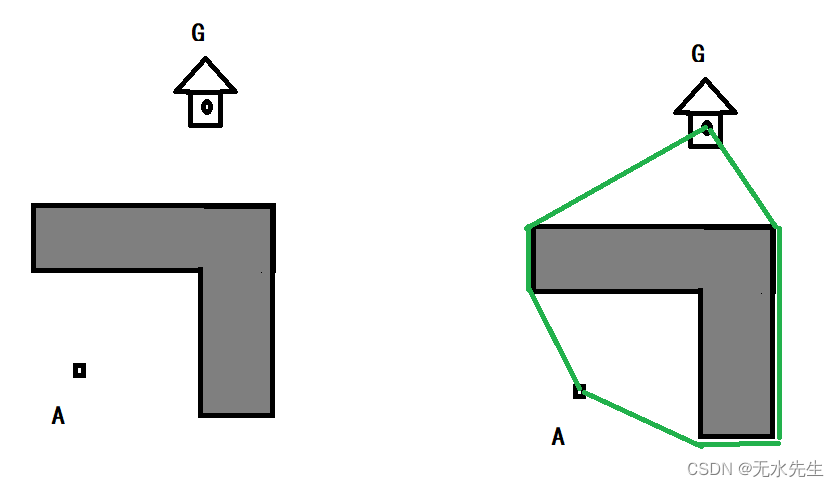
分析：（如上图）您从A，G以及楼的边角，可以抽象出（右图）绿色路径构成一个多边形。从A无论顺时针和逆时针都可以到达G，其中最短者就是最短路径。

2.2 引出凸包络问题

对于给定的若干个点，求覆盖所有点的多边形凸包络。如图：

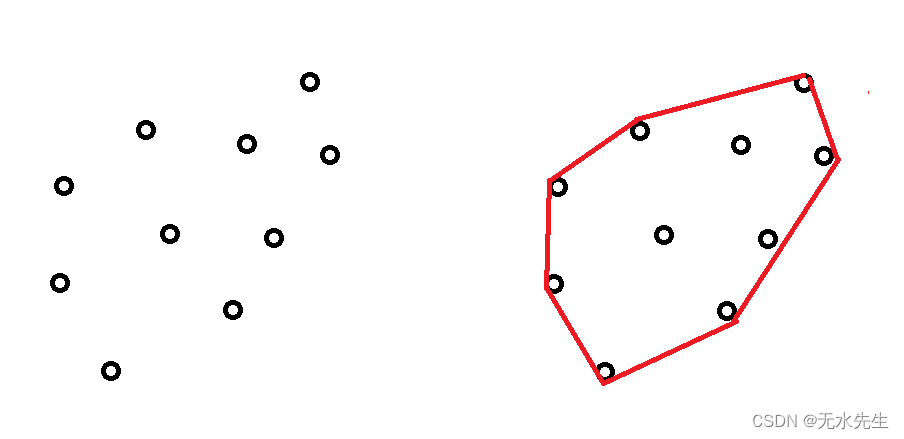
2.3 这里有必要先介绍凸包的概念

在空间上的集合Ω，如果集合内任意两个点的连线段，该线段上所有的点均在集合Ω内部，那么Ω就是一个凸集。读者按照这个定义，不难判定下图中，谁是凸集。

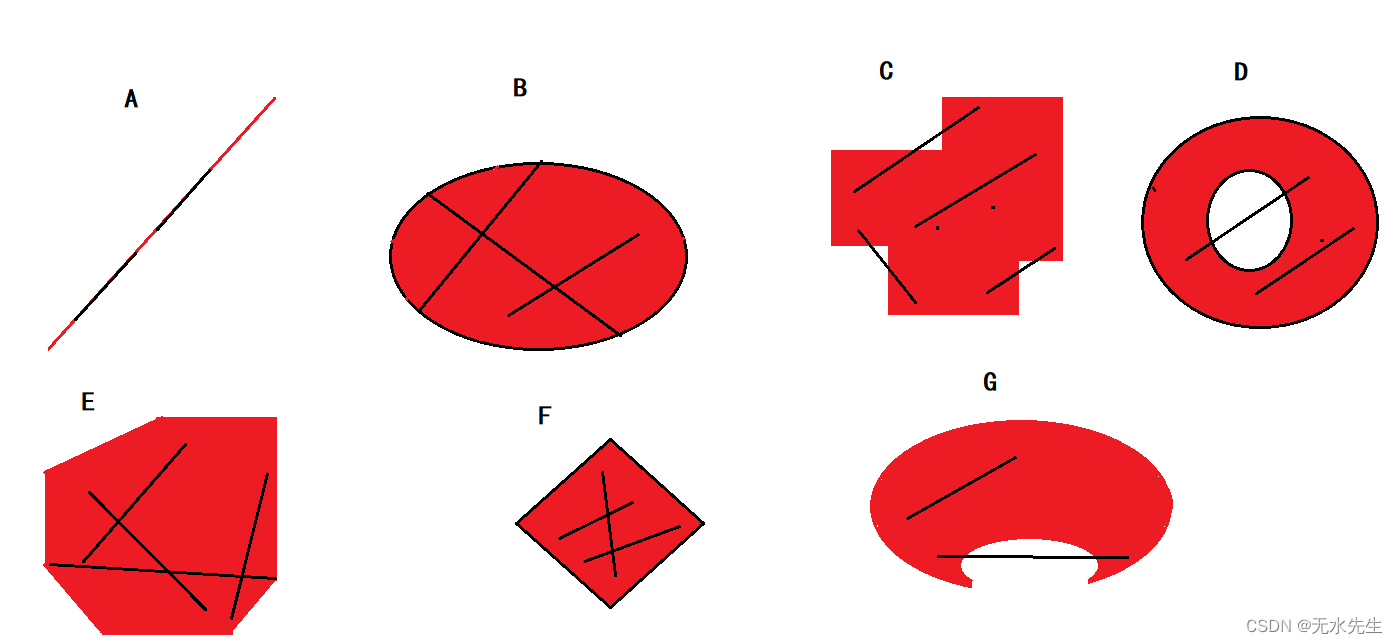
进一步说，什么是凸多边形？就是既是凸集，又是多边形的图形区域。

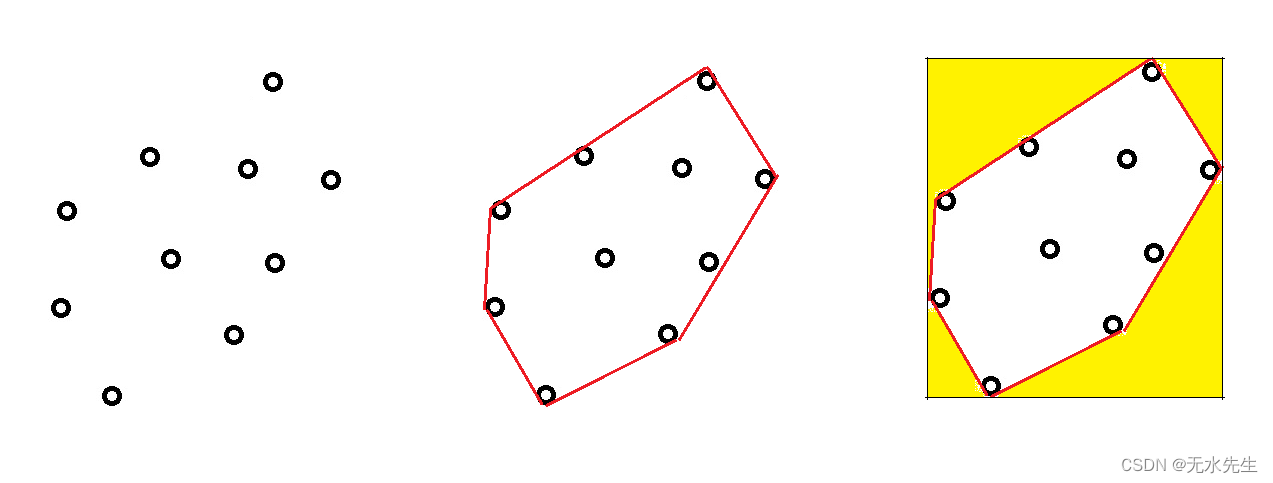
2.4 什么是Graham-Scan算法

一句话：就是从空间中一丛点中，找到覆盖它们的最小凸多边形。

A）算法描述:

Step 1) 找到一个顶点，如最左端的点.
Step 2) 循环执行：在我们不回到第一个（或最左边）点p时执行以下操作.
2.1) 下一个点q是点，使得三元组（p，q，r）对于任何其他点r都是逆时针方向。

为了找到这个点，我们简单地将 q 初始化为下一个点，然后我们遍历所有点。

对于任何点 i，如果 i 更逆时针，即 orientation(p, i, q) 是逆时针的，那么我们将 q 更新为 i。

我们 q 的最终值将是最逆时针的点。
2.2) next[p] = q（在输出凸包中存储 q 作为 p 的下一个）
2.3) p = q（将p设置为q用于下一次迭代）。

B）程序描述

Graham-Scan算法是一种灵活的凸包算法，时间复杂度是O(nlogn)
基本理念

初始化将包含凸包点的空堆栈。
选择一个起点并将其添加到堆栈中。（选出最左下角的点（排序：x最小，其次是y最小））
围绕起点到其余点做极角，按逆时针顺序对其余点进行排序。（在极角相等的情况下距离极点(p[0])最近的优先）
扫描排序的点。用叉积判断新点和栈顶头两个点形成的拐向。顺时针就弹出栈顶元素，继续判断。否则逆时针压入新点p[i]
最初将每个新点添加到堆栈中，然后检查以确保新点的外壳仍然是凸的。
删除任何创建凹角的点 - 这些点位于船体内部。（最终栈内元素就是凸包点。）

三、Graham-Scan算法代码实现

3.1 实验代码1：（c++代码）

// A C++ program to find convex hull of a set of points. Refer
// https://www.geeksforgeeks.org/orientation-3-ordered-points/
// for explanation of orientation()
#include <bits/stdc++.h>
using namespace std;struct Point
{int x, y;
};// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(Point p, Point q, Point r)
{int val = (q.y - p.y) * (r.x - q.x) -(q.x - p.x) * (r.y - q.y);if (val == 0) return 0;  // collinearreturn (val > 0)? 1: 2; // clock or counterclock wise
}// Prints convex hull of a set of n points.
void convexHull(Point points[], int n)
{// There must be at least 3 pointsif (n < 3) return;// Initialize Resultvector<Point> hull;// Find the leftmost pointint l = 0;for (int i = 1; i < n; i++)if (points[i].x < points[l].x)l = i;// Start from leftmost point, keep moving counterclockwise// until reach the start point again.  This loop runs O(h)// times where h is number of points in result or output.int p = l, q;do{// Add current point to resulthull.push_back(points[p]);// Search for a point 'q' such that orientation(p, q,// x) is counterclockwise for all points 'x'. The idea// is to keep track of last visited most counterclock-// wise point in q. If any point 'i' is more counterclock-// wise than q, then update q.q = (p+1)%n;for (int i = 0; i < n; i++){// If i is more counterclockwise than current q, then// update qif (orientation(points[p], points[i], points[q]) == 2)q = i;}// Now q is the most counterclockwise with respect to p// Set p as q for next iteration, so that q is added to// result 'hull'p = q;} while (p != l);  // While we don't come to first point// Print Resultfor (int i = 0; i < hull.size(); i++)cout << "(" << hull[i].x << ", "<< hull[i].y << ")\n";
}// Driver program to test above functions
int main()
{Point points[] = {{0, 3}, {2, 2}, {1, 1}, {2, 1},{3, 0}, {0, 0}, {3, 3}};int n = sizeof(points)/sizeof(points[0]);convexHull(points, n);return 0;
}

3.2 实验代码2：（ python代码1)

# Python3 program to find convex hull of a set of points. Refer 
# https://www.geeksforgeeks.org/orientation-3-ordered-points/
# for explanation of orientation()# point class with x, y as point 
class Point:def __init__(self, x, y):self.x = xself.y = ydef Left_index(points):'''Finding the left most point'''minn = 0for i in range(1,len(points)):if points[i].x < points[minn].x:minn = ielif points[i].x == points[minn].x:if points[i].y > points[minn].y:minn = ireturn minndef orientation(p, q, r):'''To find orientation of ordered triplet (p, q, r). The function returns following values 0 --> p, q and r are collinear 1 --> Clockwise 2 --> Counterclockwise '''val = (q.y - p.y) * (r.x - q.x) - \(q.x - p.x) * (r.y - q.y)if val == 0:return 0elif val > 0:return 1else:return 2def convexHull(points, n):# There must be at least 3 points if n < 3:return# Find the leftmost pointl = Left_index(points)hull = []'''Start from leftmost point, keep moving counterclockwise until reach the start point again. This loop runs O(h) times where h is number of points in result or output. '''p = lq = 0while(True):# Add current point to result hull.append(p)'''Search for a point 'q' such that orientation(p, q, x) is counterclockwise for all points 'x'. The idea is to keep track of last visited most counterclock- wise point in q. If any point 'i' is more counterclock- wise than q, then update q. '''q = (p + 1) % nfor i in range(n):# If i is more counterclockwise # than current q, then update q if(orientation(points[p], points[i], points[q]) == 2):q = i'''Now q is the most counterclockwise with respect to p Set p as q for next iteration, so that q is added to result 'hull' '''p = q# While we don't come to first pointif(p == l):break# Print Result for each in hull:print(points[each].x, points[each].y)# Driver Code
points = []
points.append(Point(0, 3))
points.append(Point(2, 2))
points.append(Point(1, 1))
points.append(Point(2, 1))
points.append(Point(3, 0))
points.append(Point(0, 0))
points.append(Point(3, 3))convexHull(points, len(points))# This code is contributed by 
# Akarsh Somani, IIIT Kalyani

3.3 实验代码3：（ python代码2 )

import random"""
Computes the Convex Hull with the Graham Scan algorithm
Use:h = ConvexHull()print(h.hull)
"""class ConvexHull:def __init__(self, points):if not points:self.points = [(random.randint(0,100),random.randint(0,100)) for i in range(50)]else:self.points = pointsself.hull = self.compute_convex_hull()def get_cross_product(self,p1, p2, p3):return ((p2[0] - p1[0])*(p3[1] - p1[1])) - ((p2[1] - p1[1])*(p3[0] - p1[0]))def get_slope(self,p1, p2):if p1[0] == p2[0]:return float('inf')else:return 1.0*(p1[1]-p2[1])/(p1[0]-p2[0])def compute_convex_hull(self):hull = []self.points.sort(key=lambda x:[x[0],x[1]])start = self.points.pop(0)hull.append(start)self.points.sort(key=lambda p: (self.get_slope(p,start), -p[1],p[0]))for pt in self.points:hull.append(pt)while len(hull) > 2 and self.get_cross_product(hull[-3],hull[-2],hull[-1]) < 0:hull.pop(-2)return hullimport numpy as np
import matplotlib.pyplot as pltfig = plt.figure()
ax1 = fig.add_subplot(111)
#设置标题
ax1.set_title('Scatter Plot')
#设置X轴标签
plt.xlabel('X')
#设置Y轴标签
plt.ylabel('Y')
#画散点图
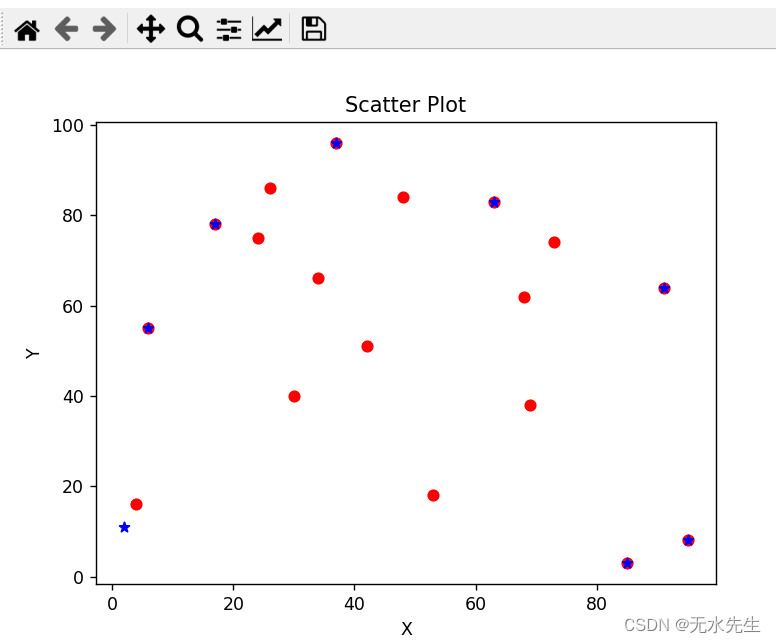
for pt in MakePoint.points:ax1.scatter(pt[0],pt[1],c = 'r',marker = 'o')
for pt in sidePoint:ax1.scatter(pt[0],pt[1],c = 'b',marker = '*')
#设置图标
plt.legend('x1')
#显示所画的图
plt.show()

测试图：

四、其它实现

4.1 用openCV进行

范例调用opencv库

import cv2
import numpy as np# 新建512*512的空白图片
img = np.zeros((512,512,3), np.uint8)
# 平面点集
pts = np.array([[200,250], [250,300], [300, 270], [270,200], [120, 240]], np.int32)
pts = pts.reshape((-1,1,2))
# 绘制填充的多边形
cv2.fillPoly(img, [pts], (255,255,255))
# 保存图片
cv2.imwrite('F://polygon.png', img)

import cv2# 读取图片并转至灰度模式
imagepath = 'F://convex.png'
img = cv2.imread(imagepath, 1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 二值化
ret, thresh = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
# 图片轮廓
image, contours, hierarchy = cv2.findContours(thresh, 2, 1)
cnt = contours[0]
# 寻找凸包并绘制凸包（轮廓）
hull = cv2.convexHull(cnt)
print(hull)length = len(hull)
for i in range(len(hull)):cv2.line(img, tuple(hull[i][0]), tuple(hull[(i+1)%length][0]), (0,255,0), 2)# 显示图片
cv2.imshow('line', img)
cv2.waitKey()

4.2 用网上一个代码，也很有趣！


import sys
import random
import matplotlibmatplotlib.use('Qt5Agg')
from PyQt5 import QtCore, QtWidgets
from PyQt5.QtGui import QIcon
from PyQt5.QtWidgets import QApplication, QMainWindow, QMenu, QVBoxLayout, QHBoxLayout, QSizePolicy, QWidget, \QTextBrowser, QLineEdit, QPushButton, QMessageBox
from matplotlib.backends.backend_qt5agg import FigureCanvasQTAgg as FigureCanvas
from matplotlib.figure import Figure
from matplotlib.animation import FuncAnimation
import matplotlib.pyplot as pltxx = [random.randint(1, 10) for i in range(10)]
yy = [random.randint(1, 10) for i in range(10)]class MyMplCanvas(FigureCanvas):def __init__(self, parent=None, width=12, height=6, dpi=100):fig = Figure(figsize=(9, 7), dpi=100)self.ax = fig.add_subplot(1, 1, 1)FigureCanvas.__init__(self, fig)self.setParent(parent)FigureCanvas.setSizePolicy(self,QtWidgets.QSizePolicy.Expanding,QtWidgets.QSizePolicy.Expanding)FigureCanvas.updateGeometry(self)class ApplicationWindow(QtWidgets.QMainWindow):def __init__(self):QtWidgets.QMainWindow.__init__(self)self.index = 0self.dic = {}self.pointsSize = 30self.upper = 100self.lower = -100self.xx = [random.randint(self.lower, self.upper) for i in range(self.pointsSize)]self.yy = [random.randint(self.lower, self.upper) for i in range(self.pointsSize)]self.points = [[self.xx[i], self.yy[i]] for i in range(self.pointsSize)]self.points.sort(key=lambda x: (x[0], x[1]))self.setAttribute(QtCore.Qt.WA_DeleteOnClose)self.setWindowTitle("分治法生成凸包演示by18070542孙泽坤")self.main_widget = QtWidgets.QWidget(self)self.xs = []self.ys = []self.pointers = 0self.game_start()vbox = QtWidgets.QVBoxLayout(self.main_widget)self.canvas = MyMplCanvas(self.main_widget, width=6, height=6, dpi=100)  ###attention###vbox.addWidget(self.canvas)hbox = QtWidgets.QHBoxLayout(self.main_widget)self.textBrowser = QTextBrowser(self)self.button = QPushButton("下一步")self.quitButton = QPushButton("退出")self.introduceButton = QPushButton("查看凸包问题原理介绍")self.introduceButton.clicked.connect(self.introduce)self.button.clicked.connect(self.choice_point)self.quitButton.clicked.connect(self.exit_pragram)vbox.addWidget(self.button)vbox.addWidget(self.quitButton)vbox.addWidget(self.introduceButton)vbox.addWidget(self.textBrowser)self.setLayout(vbox)self.main_widget.setFocus()self.setCentralWidget(self.main_widget)self.ani = FuncAnimation(self.canvas.figure, self.update_line, interval=15)self.textBrowser.append("先把最左边和最右边的两个边界点({},{})和({},{})连接起来".format(self.points[0][0], self.points[0][1], self.points[self.pointsSize - 1][0], self.points[self.pointsSize - 1][1]))def caculate(self, x1, y1, x2, y2, x3, y3):return x1 * y2 + x3 * y1 + x2 * y3 - x1 * y3 - x2 * y1 - x3 * y2def judge(self, x1, x2, y1, y2):pta = tuple([x1, y1])ptb = tuple([x2, y2])numa = self.dic.get(pta, [])numb = self.dic.get(ptb, [])if ptb in numa or pta in numb:return Falsenuma.append(ptb)numb.append(pta)self.dic[pta] = numaself.dic[ptb] = numbreturn Truedef findUpperMax(self, x1, y1, x2, y2):flag = FalseupperMax = 0upperx = uppery = 0for i in self.points:if i[0] == x1 and i[1] == y1 or i[0] == x2 and i[1] == y2:continueareaData = self.caculate(x1, y1, x2, y2, i[0], i[1])if areaData > 0:if areaData > upperMax:flag = TrueupperMax = areaDataupperx = i[0]uppery = i[1]if flag == False:if self.judge(x1, x2, y1, y2) == False:returnself.xs.append([x1, x2])self.xs.append([y1, y2])returnif self.judge(x1, upperx, y1, uppery) == False:returnself.xs.append([x1, upperx])self.xs.append([y1, uppery])if self.judge(x2, upperx, y2, uppery) == False:returnself.xs.append([x2, upperx])self.xs.append([y2, uppery])self.findUpperMax(x1, y1, upperx, uppery)self.findUpperMax(upperx, uppery, x2, y2)def findBottomMin(self, x1, y1, x2, y2):flag = FalselowerMax = 0lowerx = lowery = 0for i in self.points:if i[0] == x1 and i[1] == y1 or i[0] == x2 and i[1] == y2:continueareaData = self.caculate(x1, y1, x2, y2, i[0], i[1])if areaData < 0:if areaData < lowerMax:flag = TruelowerMax = areaDatalowerx = i[0]lowery = i[1]if flag == False:if self.judge(x1, x2, y1, y2) == False:returnself.xs.append([x1, x2])self.xs.append([y1, y2])returnif self.judge(x1, lowerx, y1, lowery) == False:returnself.xs.append([x1, lowerx])self.xs.append([y1, lowery])if self.judge(x2, lowerx, y2, lowery) == False:returnself.xs.append([x2, lowerx])self.xs.append([y2, lowery])self.findBottomMin(x1, y1, lowerx, lowery)self.findBottomMin(lowerx, lowery, x2, y2)def scatter_points(self):self.canvas.ax.plot([self.points[0][0], self.points[self.pointsSize - 1][0]],[self.points[0][1], self.points[self.pointsSize - 1][1]], color='black')for i in range(0, self.pointsSize):self.canvas.ax.scatter(self.xx[i], self.yy[i], color='k', s=20)def game_start(self):self.findUpperMax(self.points[0][0], self.points[0][1], self.points[self.pointsSize - 1][0],self.points[self.pointsSize - 1][1])self.findBottomMin(self.points[0][0], self.points[0][1], self.points[self.pointsSize - 1][0],self.points[self.pointsSize - 1][1])def choice_point(self):self.textBrowser.clear()if self.pointers == len(self.xs):self.textBrowser.append("凸包生成完毕！点击退出键退出")returnself.ys.append(self.xs[self.pointers])self.ys.append(self.xs[self.pointers + 1])# print(self.xs[self.pointers][0], self.xs[self.pointers + 1][0],#             self.xs[self.pointers][1], self.xs[self.pointers + 1][1])text = "选择点({0},{1})和点({2},{3})，把它们连接起来" \.format(self.xs[self.pointers][0], self.xs[self.pointers + 1][0],self.xs[self.pointers][1], self.xs[self.pointers + 1][1])self.textBrowser.append(text)self.pointers += 2def update_line(self, i):self.canvas.ax.clear()self.scatter_points()for i in range(0, len(self.ys), 2):a = self.ys[i]b = self.ys[i + 1]if i == len(self.ys) - 2:self.canvas.ax.plot(a, b, color='red')else:self.canvas.ax.plot(a, b, color='black')if i == len(self.ys) - 2:self.canvas.ax.scatter(self.ys[i][0], self.ys[i + 1][0], color='red')self.canvas.ax.scatter(self.ys[i][1], self.ys[i + 1][1], color='red')def introduce(self):text = "第一步：把所有点在横坐标方向上按从小到大顺序排列，左右两个端点必定是凸包上的点\n第二步：在上凸包集合点中找一个距离直线最远的点，将它与左右端点连接起来\n第三步：重复递归求解到上半凸包的边\n第四步：下半凸包同理，通过递归求解，最终得到整个凸包"reply = QMessageBox.information(self, '分治法凸包问题原理介绍', text, QMessageBox.Yes)def exit_pragram(self):sys.exit(0)if __name__ == "__main__":App = QApplication(sys.argv)aw = ApplicationWindow()aw.show()App.exit()sys.exit(App.exec_())