前置知识
注意力机制
见 这篇
二维 TSP 问题
给定二维平面上 nnn 个点的坐标 S={xi}i=1nS=\{x_i\}_{i=1}^nS={xi}i=1n,其中 xi∈[0,1]2x_i\in [0,1]^2xi∈[0,1]2,要找到一个 1∼n1\sim n1∼n 的排列 π\piπ ,使得目标函数
L(π∣s)=∥xπ1−xπn∥2+∑i=1n−1∥xπi−xπi+1∥2L(\pi|s)=\Vert x_{\pi_1}-x_{\pi_n} \Vert_2+\sum_{i=1}^{n-1}\Vert x_{\pi_{i}}-x_{\pi_{i+1}}\Vert_2L(π∣s)=∥xπ1−xπn∥2+i=1∑n−1∥xπi−xπi+1∥2
尽可能小。
Pointer Networks
论文链接
随意选择 π1\pi_1π1 ,然后依次预测 π2,π3,...,πn\pi_2,\pi_3,...,\pi_nπ2,π3,...,πn 。
预测方式利用了注意力机制(加性模型):
uji=vTtanh(W1ej+W2di)u_j^i=v^T\tanh(W_1e_j+W_2d_i)uji=vTtanh(W1ej+W2di)
其中 v,W1,W2v,W_1,W_2v,W1,W2 是可学习的参数,eje_jej 是(节点 jjj 的)encoder 隐状态,did_idi 是(已选 i−1i-1i−1 个点的图的) decoder 隐状态。然后,直接将 softmax 后的 uiu^iui 作为输出:
P(πi∣π1:i−1,P)=softmax(ui)P(\pi_i|\pi_{1:i-1},\mathcal{P})=\text{softmax}(u^i)P(πi∣π1:i−1,P)=softmax(ui)
encoder 和 decoder 的实现使用了单层 LSTM,训练使用 SGD。
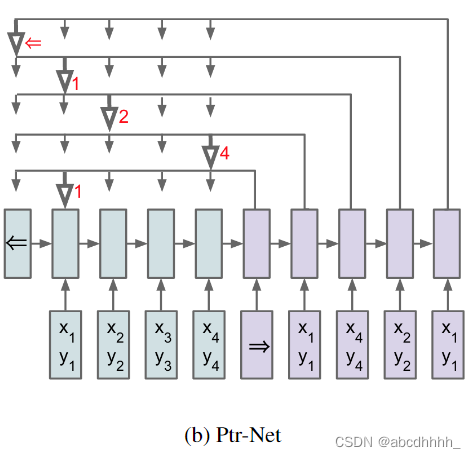
效果如下:
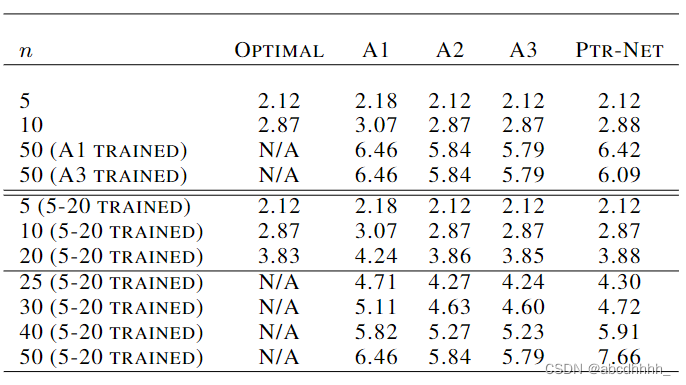
传统的 RNN 的输出是固定词汇表上的分布,因此不能应对 nnn 比训练集大的情况。而 Pointer Networks 的输出是输入序列上的分布,因此可以应对任意大小的 nnn 。
Attention, Learn to Solve Routing Problems!
论文链接
引入强化学习,学习策略函数 pθ(π∣s)=∏t=1npθ(πt∣s,π1:t−1)p_{\theta}(\pi|s)=\prod_{t=1}^np_{\theta}(\pi_t|s,\pi_{1:t-1})pθ(π∣s)=∏t=1npθ(πt∣s,π1:t−1)。
encoder 和 decoder 套用 Transformer 结构。