一. Actor Critic

1.基本概念
Actor Critic 为类似于Policy Gradient 和 Q-Learning 等以值为基础的算法的组合。

a. 其中Actor 类似于Policy Gradient，以状态s为输入，神经网络输出动作actions，并从在这些连续动作中按照一定的概率选取合适的动作action。
b. Critic 类似于 Q-Learning 等以值为基础的算法，由于在Actor模块中选择了合适的动作action，通过与环境交互可得到新的状态s_, 奖励r，将状态 s_作为神经网络的输入，得到v_，而原来的状态s通过神经网络输出后得到v。
c. 通过公式$ \ td_{error}= r+\gamma v_{-} \ - v$得到状态之间的差 $t{d}_{error}$，最后通过状态s，动作action，以及误差 $t{d}_{e}rror$ 更新Actor网络的参数，实现单步更新。
d. 将s_ 状态赋予给 s 状态。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EvkooAOX-1581478026600)(https://morvanzhou.github.io/static/results/reinforcement-learning/6-1-1.png)]
所以，Actor Critic 结合了 Policy Gradient（Actor）和 Function Approximation Critic）。Actor 基于概率选择行为，Critic 基于 Actor 的行为评判行为的得分，Actor 根据 Critic 的评分修改选择行为。

**Actor Critic 方法的优势：**可以进行单步更新，比传统的Policy Gradient 要快。
**Actor Critic 方法的劣势：**取决于Critic的价值判断，但是Critic难收敛，再加上Actor的更新，就更难收敛了。为了解决收敛的问题，有改进版的 Deep Deterministic Policy Gradient （DDPG），不仅仅融合了DQN的优势，同时解决了难收敛的问题。

2.代码框架
Actor：

class Actor(object):def __init__(self, sess, n_features, n_actions, lr=0.001):# 用 tensorflow 建立 Actor 神经网络,# 搭建好训练的 Graph.def learn(self, s, a, td):# s, a 用于产生 Gradient ascent 的方向,# td 来自 Critic, 用于告诉 Actor 这方向对不对.def choose_action(self, s):# 根据 s 选 行为 a

Critic

class Critic(object):def __init__(self, sess, n_features, lr=0.01):# 用 tensorflow 建立 Critic 神经网络,# 搭建好训练的 Graph.def learn(self, s, r, s_):# 学习 状态的价值 (state value), 不是行为的价值 (action value),# 计算 TD_error = (r + v_) - v,# 用 TD_error 评判这一步的行为有没有带来比平时更好的结果,# 可以把它看做 Advantagereturn # 学习时产生的 TD_error

Actor 想要最大化期望的 reward，在Actor Critic算法中，我们用“比平常好多少”（td_error）来当做reward，所以就是：

with tf.variable_scope('exp_v'):log_prob = tf.log(self.acts_prob[0, self.a])    # log 动作概率self.exp_v = tf.reduce_mean(log_prob * self.td_error)   # log 概率 * TD 方向
with tf.variable_scope('train'):# 因为我们想不断增加这个 exp_v (动作带来的额外价值),# 所以我们用过 minimize(-exp_v) 的方式达到# maximize(exp_v) 的目的self.train_op = tf.train.AdamOptimizer(lr).minimize(-self.exp_v)

Critic 更新很简单，就是像Q Learning 那样更新现实和估计的误差(td_error)就好了

with tf.variable_scope('squared_TD_error'):self.td_error = self.r + GAMMA * self.v_ - self.vself.loss = tf.square(self.td_error)    # TD_error = (r+gamma*V_next) - V_eval
with tf.variable_scope('train'):self.train_op = tf.train.AdamOptimizer(lr).minimize(self.loss)

完整代码见：莫烦PYTHON Actor Critic

二. Deep Deterministic Policy Gradient (DDPG)

1.基本概念

DDPG 可以分为 ‘DEEP’ 和 ‘Deterministic Policy Gradient’，然后‘Deterministic Policy Gradient’ 又能被细分为 ‘Deterministic’ 和 ‘Policy Gradient’。

其中 DEEP 就是走向更深层次，使用一个记忆库和俩套结构相同，但是参数更新频率不同的神经网络有效促进学习。采用的神经网络类似于DQN，但是DDPG的神经网络形式比DQN要复杂一点点。

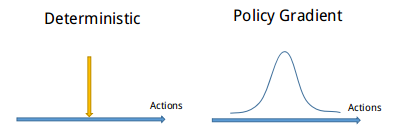
接着是 Deterministic Policy Gradient，如上图所示，相比其他强化学习方法，Policy gradient 能被用来在连续动作上进行动作的筛选，而且筛选的时候是根据所学习到的动作分布随机进行筛选。而Deterministic 改变了输出动作的过程，旨在连续动作上输出一个动作值。

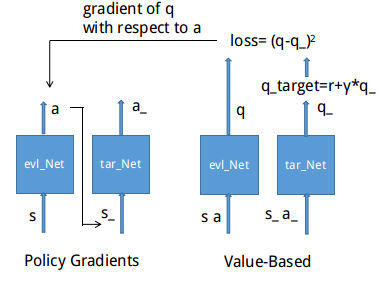
DDPG用到的神经网络是怎么样的？它其实有点类似于Actor-Critic，也需要有基于策略Policy 的神经网络 和 基于价值 Value 的神经网络，但是为了体现DQN的思想，每种神经网络我们都需要再细分成俩个。Policy Gradient 这边有估计网络和现实网络，估计网络用来输出实时的动作，而现实网络则是用来更新价值网络系统的。再看看价值系统这边，我们也有现实网络和估计网络，他们都在输出这个状态的价值，而输入端却有不同，状态现实网络这边会拿着当时actor施加的动作当做输入。在实际运用中，DDPG的这种做法的确带来了更有效的学习过程。

$\triangledown_{\theta \mu J}\approx \frac{1}{N}\sum_{i}\triangledown_{a}Q(s,a|\theta^{Q})|{s=s{i},a=u(s_{i})} \bigtriangledown_{\theta \mu}\mu(s|\theta^{u})|s_{i} $

DDPG 的更新公式可从上面得出，关于Actor 部分，他的参数更新会涉及到 Critic， 上面是关于 Actor 参数的更新，它的前半部分 grad[Q] 是从Critic 来的，阐述了Actor 的动作要怎么移动，才能获得更大的 Q。而后半部分 grad[u] 是从Actor来的，阐述了 Actor 要怎么样修改自身参数，才使得Actor 有可能做这个动作，所以俩者阐述了Actor 要朝着更有可能获取Q的方向修改动作参数。

2.代码框架
Actor:

#Building network, same architecture but with different parametersdef _build_net(self, s, scope, trainable):   with tf.variable_scope(scope):init_w = tf.contrib.layers.xavier_initializer()init_b = tf.constant_initializer(0.001)net = tf.layers.dense(s, 100, activation=tf.nn.relu,kernel_initializer=init_w, bias_initializer=init_b, name='l1',trainable=trainable)net = tf.layers.dense(net, 20, activation=tf.nn.relu,kernel_initializer=init_w, bias_initializer=init_b, name='l2',trainable=trainable)with tf.variable_scope('a'):actions = tf.layers.dense(net, self.a_dim, activation=tf.nn.tanh, kernel_initializer=init_w,name='a', trainable=trainable)   #action [-1,1]scaled_a = tf.multiply(actions, self.action_bound, name='scaled_a')  # Scale output to -action_bound to action_boundreturn scaled_adef learn(self, s):   # batch updateself.sess.run(self.train_op, feed_dict={S: s})if self.t_replace_counter % self.t_replace_iter == 0:self.sess.run([tf.assign(t, e) for t, e in zip(self.t_params, self.e_params)])  #Assign the latter value to the former valueself.t_replace_counter += 1def choose_action(self, s): # after traineds = s[np.newaxis, :]    # single state  np.newaxis:[1,2,3,4,5]->[[1,2,3,4,5]]return self.sess.run(self.a, feed_dict={S: s})[0]  # single actiondef add_grad_to_graph(self, a_grads): #gradientwith tf.variable_scope('policy_grads'):self.policy_grads = tf.gradients(ys=self.a, xs=self.e_params, grad_ys=a_grads)with tf.variable_scope('A_train'):opt = tf.train.RMSPropOptimizer(-self.lr)  # (- learning rate) for ascent policyself.train_op = opt.apply_gradients(zip(self.policy_grads, self.e_params))

Critic:

class Critic(object):def __init__(self, sess, state_dim, action_dim, learning_rate, gamma, t_replace_iter, a, a_):self.sess = sessself.s_dim = state_dimself.a_dim = action_dimself.lr = learning_rateself.gamma = gammaself.t_replace_iter = t_replace_iterself.t_replace_counter = 0with tf.variable_scope('Critic'):# Input (s, a), output qself.a = aself.q = self._build_net(S, self.a, 'eval_net', trainable=True)# Input (s_, a_), output q_ for q_targetself.q_ = self._build_net(S_, a_, 'target_net', trainable=False)    # target_q is based on a_ from Actor's target_netself.e_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic/eval_net')self.t_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic/target_net')with tf.variable_scope('target_q'):self.target_q = R + self.gamma * self.q_   #real value, which is treated as ground trurhwith tf.variable_scope('TD_error'):self.loss = tf.reduce_mean(tf.squared_difference(self.target_q, self.q))with tf.variable_scope('C_train'):self.train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)with tf.variable_scope('a_grad'):self.a_grads = tf.gradients(self.q, a)[0]

其实总的思路是为：

1. 始化机器人所处的位置s，通过DEEP模块(使用神经网络)输出动作a，由于有了动作a，我们自然可以根据环境预测状态s_, 而通过状态s_, 我们再一次可以得到a_

2.得到状态s, s_, a, a_ 后，在Deterministic Policy Gradient模块中，我们可以计算出q 和 q_, 然后我们可以通过公式得到q真实值 $target_q: target_{-}q=r+\gamma*q_{-} $, 通过代价函数 $loss=(targe{t}_{-}q-q{)}^2$, 其中从q = tf.layers.dense(net, 1, kernel_initializer=init_w, bias_initializer=init_b, trainable=trainable) 可以看出，q的维度为1。

3.通过代价函数以及反向传播，可以得到q对a的导数即a_grads，紧接着通过链式法则，可以求出a对DEEP模块中神经网络参数的梯度，并进行参数更新。而对于target_net 中的网络，并非实时更新，而是通过一定频率的从 evl_net 中拷贝参数给 target_net 。

整个过程基本上就是这个样子，但是至于怎么跟环境交互。个人觉得这个是比较难的。

三. Asynchronous Advantage Actor-Critic (A3C)

1. 基本概念
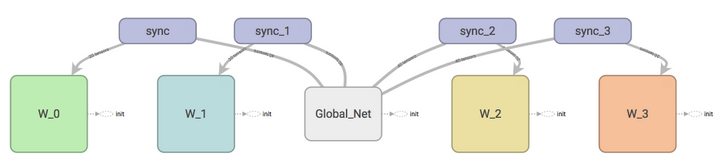
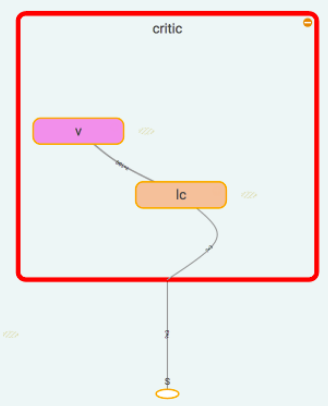
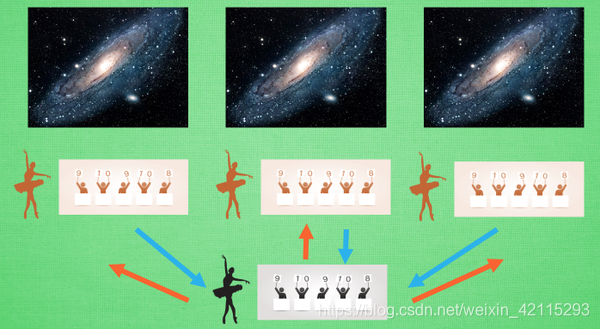
A3C 其实采用了Actor-Critic 的形式，但是引入了并行计算的概念。为了训练一对Actor 和 Critic，我们将Actor 和 Critic 复制成多份，然后放在不同的核中进行训练。其中需要声明一个主要的Actor-Critic (global)，不断从多个副本中更新的参数进行学习，获得新的参数，同时副本中的参数也不断从 Actor-Critic (global) 中获得并更新。

A3C 是Google DeepMind 提出的一种解决 Actor Critic 不收敛问题的算法。A3C会创建多个并行的环境，让多个拥有副结构的 agent 同时在这些并行环境上更新主结构中的参数。并行中的 agent 们互不干扰，而主结构的参数更新受到副结构提交更新的不连续性干扰，所以更新的相关性被降低，收敛性提高。

2. 伪代码（pseudocode）

3. 代码结构（pseudocode）
为了实现A3C, 我们要有俩套体系，可以看做中央大脑拥有global net 和它的参数，每位玩家有一个 global net 的副本 local net，可以定时向global net 推送更新，然后定时从global net获得综合版的更新，如下所示:

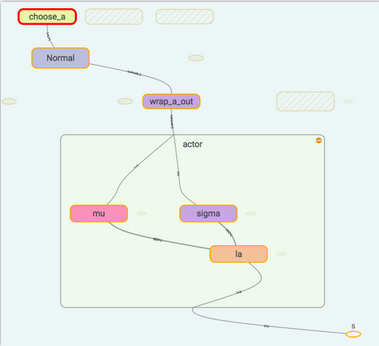
在 [莫凡PYTHON A3C](https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/6-3-A3C /)使用了Normal distribution 来选择动作，所以在搭建神经网络的时候，actor 要输出动作的均值和方差，然后放入Normal distribution 来选择动作。计算actorloss 的时候我们还需要使用到critic 提供的TD_error 作为gradient ascent 的导向。

Critic 比较简单，只需要得到他对于state的价值就行了，用于计算TD_error

具体代码见 莫凡PYTHON Asynchronous Advantage Actor-Critic (A3C)