LED的电路图
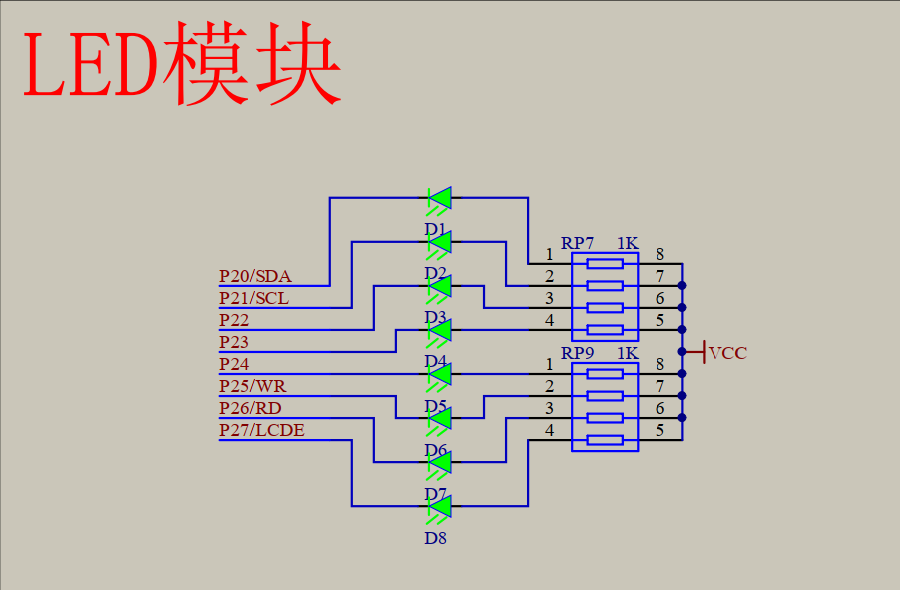
通过原理图看出,LED灯是接单片机芯片的P20~P27的
一共有8个LED,51单片机也是8字节的
P2=0x01
0xFE————1111 1110
P2=0xFE可以表示把在P2端的第一个灯点亮
1 表示高电平
0表示低电平
当为0的时候形成一个完整回路,电流从高电平流向低电平
所以我们要把LED灯对应的引脚置为0,这样就可以点亮LED灯了
点亮第一个LED灯
我们知道了点亮LED灯需要把对应的引脚置为0,下面我们来通过代码实现


从图片我们可以看出,我们确实点亮了第一个LED灯
那么我们点亮全部的LED灯的操作一个是 0000 0000 对应的16进制是0x00


我们现在通过控制P2端的8个位来控制LED灯,我们也可以通过控制一个位来控制灯的亮灭



这两个操作,都可以将第五个LED灯点亮
LED灯的闪烁
通常我们在大街小巷可以看到闪烁的LED灯,然后他们的闪烁周期也不相同,我们如何通过单片机控制
我们引入时间延时的概念
时间延时的设置我们可以在STC-ISP生成
我们来演示一下
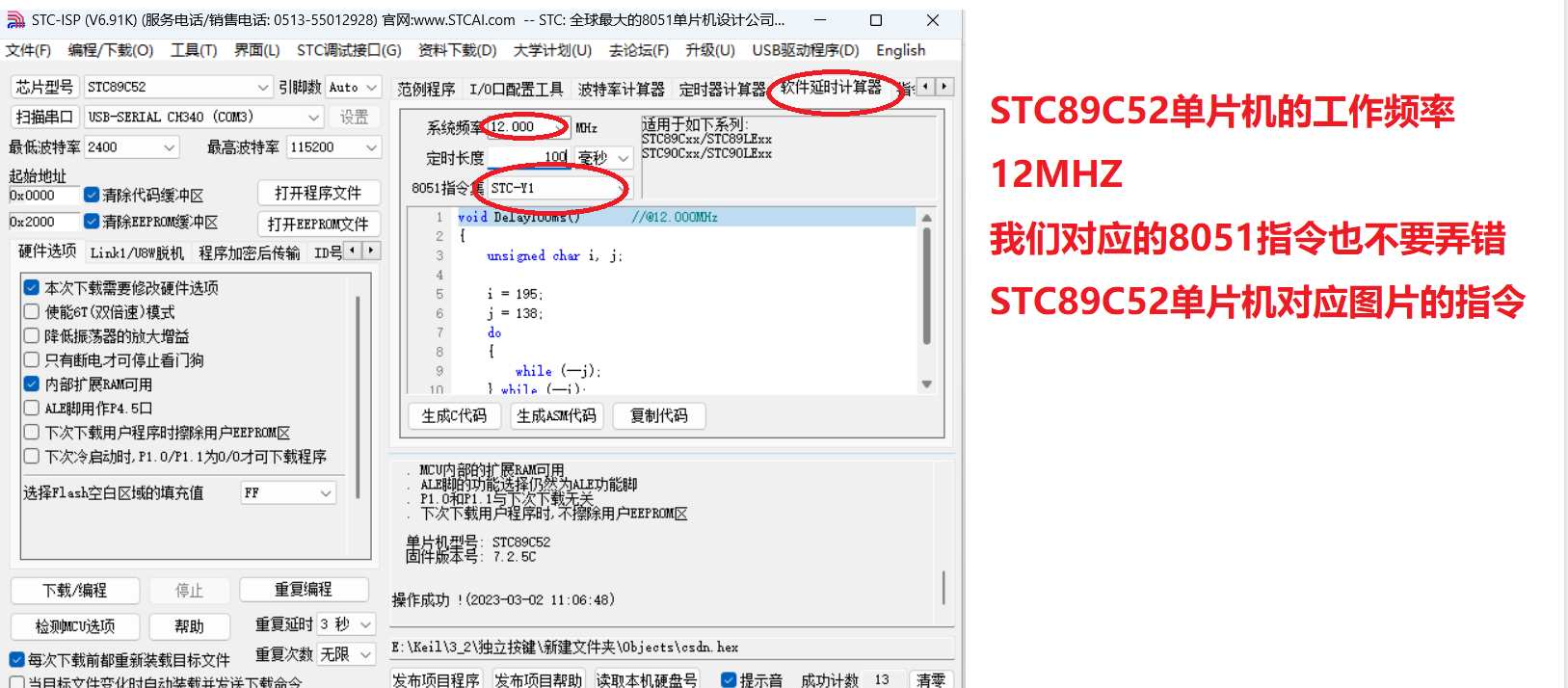
生成了代码我们拷贝到软件上
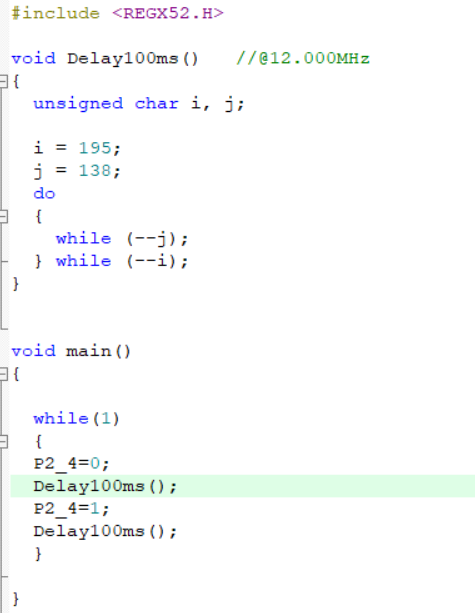
这个代码就可以不停的闪烁我们的第五个LED灯
我们设计不同周期的闪烁每次都去STC-ISP生成会比较麻烦,那么我们是不是可以设计一个自定义的函数来实现你想要的闪烁时间
自定义延时的设计
首先我们在STC-ISP生成一个1毫秒的延时
void Delay1ms() //@12.000MHz
{unsigned char i, j;i = 2;j = 239;do{while (--j);} while (--i);
}我们通过修改这个1毫秒的延时来实现
#include <REGX52.H>void Delay(long xms) //@12.000MHz
{unsigned char i, j;while(xms--){i = 2;j = 239;do{while (--j);} while (--i);}
}void main()
{while(1){P2_4=0;Delay(500);P2_4=1;Delay(500);}}我们怎么设计的呢,通过传一个常量,常量表示多少毫秒,然后传入1毫秒的函数,让这个函数循环1毫秒的延时,这样就可以做到,自定义延时了
独立按键
了解按键工作的时候,我们先看看它的电路原理图

通俗的说就是当你摁下开关,开关接通,松开开关,开关断开
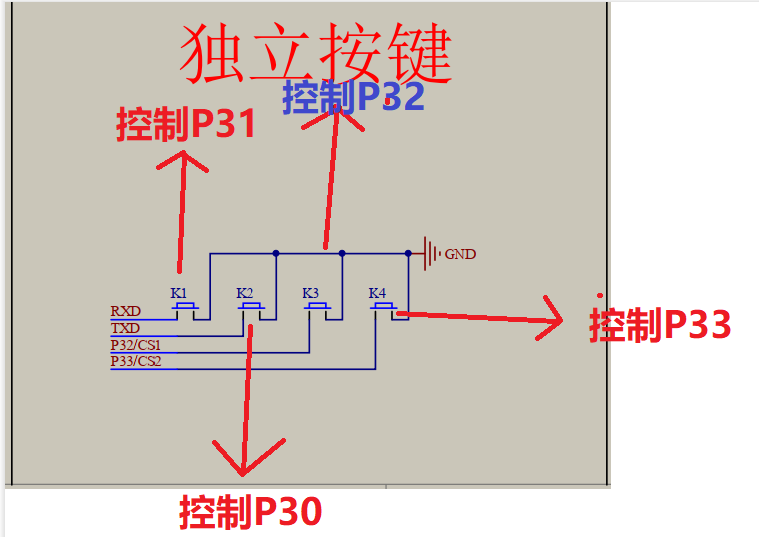
下面我们来编写程序来实现利用独立按键控制灯的亮灭

这个程序的作用就是按一下独立按钮然后第一个灯就亮了
上面就是独立按钮和LED灯的使用
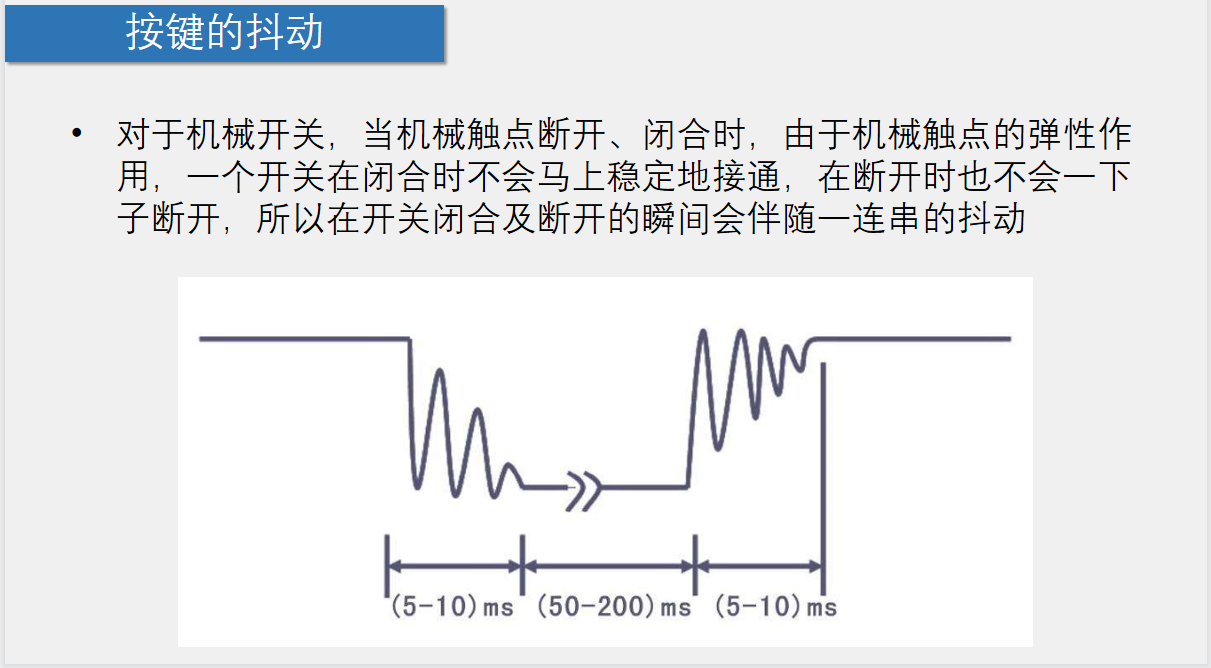
我们如何避免按键的抖动呢,我们可以通过时间延时来消除,按键抖动时的不稳定接通
void Delay(long xms) //@12.000MHz
{unsigned char i, j;while(xms){i = 2;j = 239;do{while (--j);} while (--i);xms--;}
}void main()
{while(1){P2_0=1;if(P3_1==0){Delay(10);while(P3_1==0);Delay(5);P2_0=0;Delay(500);}}
}
LED灯的使用与按钮

#include <REGX52.H>void Delay(long xms) //@12.000MHz
{unsigned char i, j;while(xms){i = 2;j = 239;do{while (--j);} while (--i);xms--;}
}void main()
{while(1){int i=0;int j=0;int ret1=1;int ret2=0x80;for(i=0;i<8;i++){P2=~(ret1<<i);Delay(500);}for(j=0;j<8;j++){P2=~(ret2>>j);Delay(500);}}
}
功能:LED灯从第一个灯依次到第八个灯亮,然后再从第八个灯亮到第一个灯(倒着)