【C++】map和set的封装（红黑树）

news/2024/12/29 2:18:39/

map和set的封装

  • 一、介绍
  • 二、stl源码剖析
  • 三、仿函数获取数值
  • 四、红黑树的迭代器
  • 五、map的[]
    • 5.1 普通迭代器转const迭代器
  • 六、set源码
  • 七、map源码
  • 八、红黑树源码

一、介绍

首先要知道map和set的底层都是用红黑树实现的
【数据结构】红黑树
set只需要一个key，但是map既有key也有val。
那么我们怎么同时兼容呢？

二、stl源码剖析

在这里插入图片描述

从这张图可以看出红黑树的节点里面存的类型是由Value决定的，跟Key无关。

所以我们实现的时候就可以给RBTree添加一个模板参数

template<class K, class T>
class RBTree

T模板参数我们既可以传K也可以传pair<k, V>
map：

template <class K>
class set
{
private:RBTree<K,K> _t;
};

set：

template <class K, class V>
class map
{
private:RBTree<K, pair<const K,V>> _t;
};

既然通过第二个参数就能确定节点的类型，那么第一个参数有什么用呢?

当我们查找的时候，如果是map，第二个参数就是pair类型，不能使用，所以得加上第一个参数，方便查找。

参照stl的方法定义节点：

template <class T>
struct RBTreeNode
{RBTreeNode(const T& data): _data(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}T _data;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;
};

三、仿函数获取数值

我们知道红黑树是搜索树，插入的时候需要比较大小，而我们插入的有可能是K，也有可能是pair<K, V>，导致我们无法直接比较。

而stl的做法就是利用仿函数获取我们需要进行比较的元素。
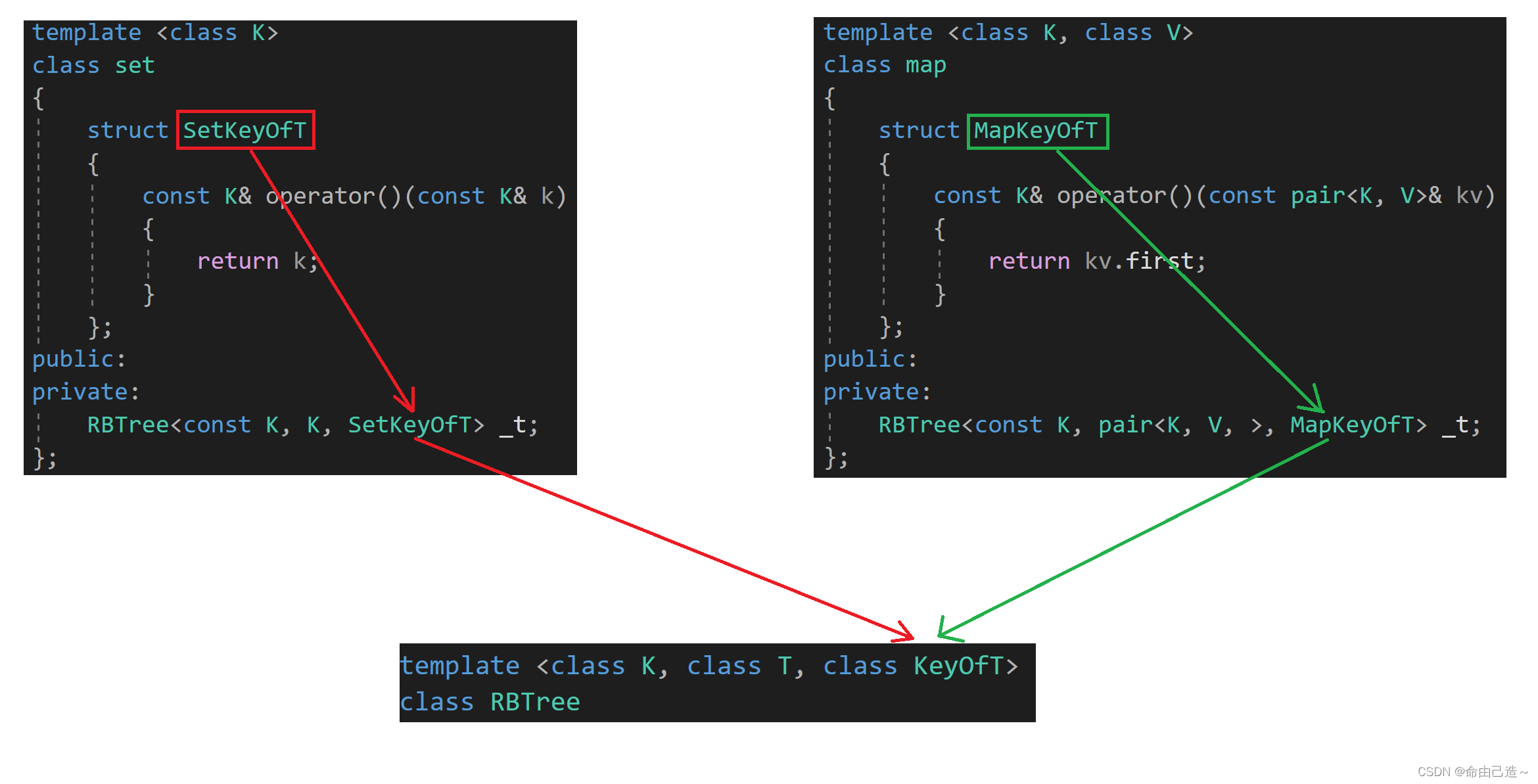
在这里插入图片描述
set：

template <class K>
class set
{struct SetKeyOfT{const K& operator()(const K& k){return k;}};
public:
private:RBTree<K, K, SetKeyOfT> _t;
};

map：

template <class K, class V>
class map
{struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};
public:
private:RBTree<K, pair<K, V, >, MapKeyOfT> _t;
};

在这里插入图片描述
进行大小比较

KeyOfT kot;// 仿函数比较
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_left;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_right;}else return false;
}

四、红黑树的迭代器

template <class T, class Ref, class Ptr>
struct RBTIterator
{typedef RBTreeNode<T> Node;typedef RBTIterator<T, Ref, Ptr> self;RBTIterator(Node* node): _node(node){}Node* _node;
};

*：解引用操作，返回对应结点数据的引用:

Ref operator*()
{return _node->_data;
}

->：访问成员操作符，返回节点数据的地址

Ptr operator->()
{return &_node->_data;
}

!=、== 比较迭代器是否指向同一节点

bool operator!=(const self& it)
{return _node != it._node;
}bool operator==(const self& it)
{return _node == it._node;
}

begin() 和 end()
begin()：返回的是最左节点（中序遍历的第一个节点）
end()：迭代器的end()一般是返回最后一个节点的下一个位置，这里设置为nullptr。

typedef RBTIterator<T, T&, T*> iterator;
typedef RBTIterator<T, const T&, const T*> const_iterator;
iterator begin()
{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);
}iterator end()
{return iterator(nullptr);
}

map里面的begin()与end()

typedef typename RBTree<K, pair<const K, V>, MapKeyOfT >::iterator iterator;
iterator begin()
{return _t.begin();
}iterator end()
{return _t.end();
}

这里注意因为编译的时候编译器不知道RBTree<K, pair<const K, V>, MapKeyOfT >::iterator这是个类型还是静态成员变量，会编译出错，加上typename就是告诉编译器这里是一个类型。

set的begin()和end()

typedef typename RBTree<K, K, SetKeyOfT >::iterator iterator;
iterator begin()
{return _t.begin();
}iterator end()
{return _t.end();
}

这里重要的是迭代器的++和--
++：
寻找中序遍历的下一个节点：
1️⃣ 如果右子树不为空，++就是找右子树的最左节点。
1️⃣ 如果右子树为空，++就是找祖先（孩子是父亲的左的那个祖先）

self& operator++()
{if (_node->_right){Node* min = _node->_right;while (min->_left){min = min->_left;}_node = min;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_right == cur){cur = parent;parent = parent->_parent;}_node = parent;}return *this;
}

--：
跟++刚好是反过来：
1️⃣ 如果左子树不为空，++就是找左子树的最右节点。
1️⃣ 如果左子树为空，++就是找祖先（孩子是父亲的右的那个祖先）

self& operator--()
{if (_node->_left){Node* max = _node->_left;while (max && max->_right){max = max->_right;}_node = max;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_left == cur){cur = parent;parent = parent->_parent;}_node = parent;}return *this;
}

这里还有一个重要的问题：
如果这么写那么set的值也可以被修改。那么如何保证set不能被修改呢？

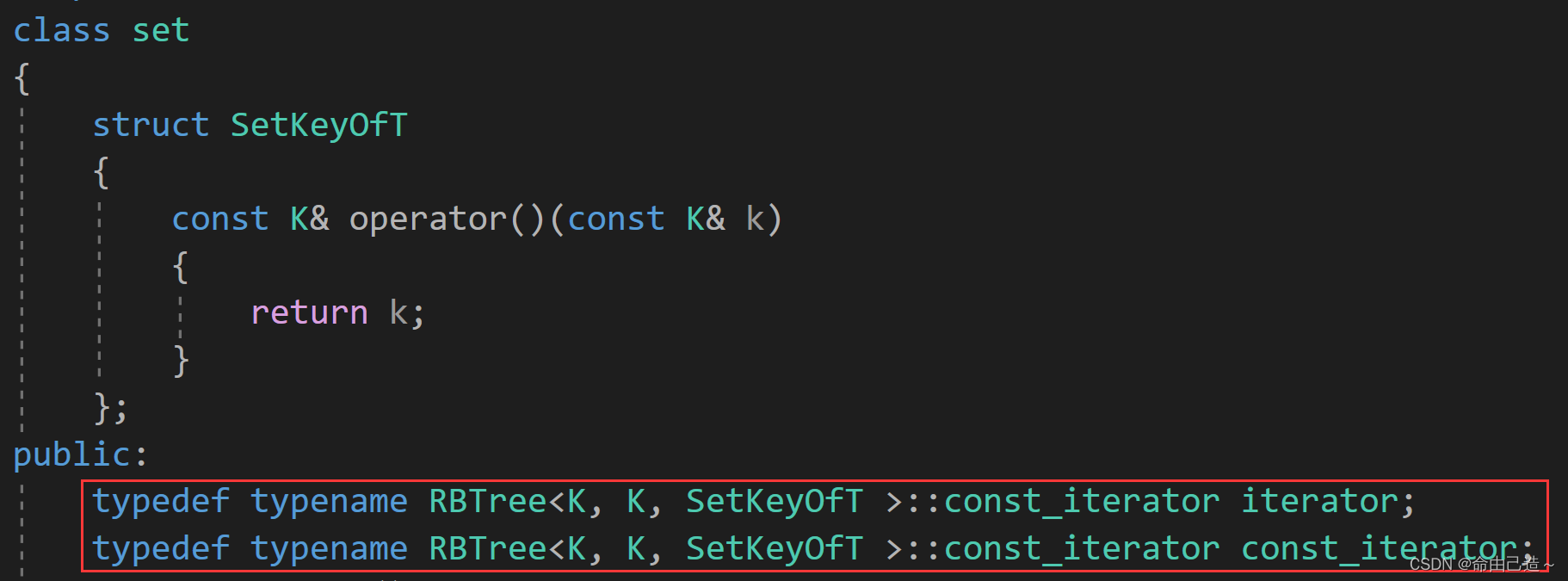
在这里插入图片描述
可以直接把普通迭代器和const迭代器都变成const_iterator。

此时这里会出现问题：

iterator begin()
{return _t.begin();
}iterator end()
{return _t.end();
}

这里_t是普通对象，会调用普通的迭代器，类型不同，无法返回。
在这里插入图片描述

我们只需要在函数后面加上const就可以权限缩小，变成const对象。

iterator begin() const
{return _t.begin();
}iterator end() const
{return _t.end();
}

在红黑树中也要加入对应的const版本begin()和end()

const_iterator begin() const
{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);
}const_iterator end() const
{return const_iterator(nullptr);
}

五、map的[]

当我们想使用map来统计次数的时候，就需要重载[]。
如果想要支持[]，那么insert的返回值就得设置成pair<iterator, bool>。
如果在bool就是false，iterator返回当前节点。

return make_pair(iterator(cur), false);

不在就插入。

return make_pair(iterator(newnode), true);

map：

V& operator[](const K& key)
{pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;
}

这里要注意set：

pair<iterator, bool> insert(const K& k)
{return _t.insert(k);
}

这里的iterator其实是const_iterator，所以导致类型不同。

5.1 普通迭代器转const迭代器

正常情况下普通迭代器不能转化为const迭代器。
为了解决这种情况，我们在迭代器内添加一个拷贝构造即可。
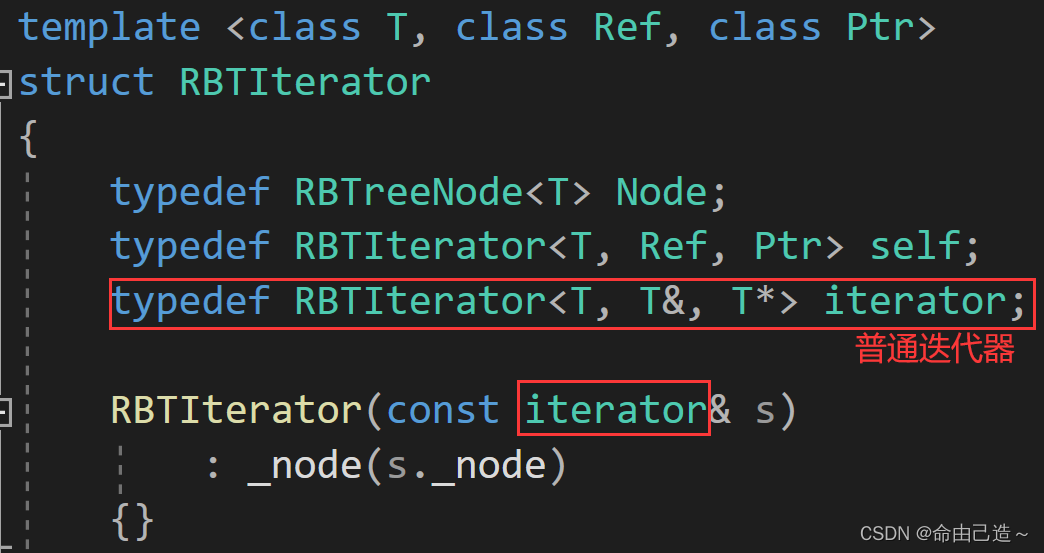
在这里插入图片描述

1️⃣ 当传进来的是普通迭代器的时候，iterator是普通迭代器，这个函数相当于拷贝构造
2️⃣ 当传进来的是const迭代器的时候，iterator依然是普通迭代器，此时该函数就相当于构造函数（普通迭代构造const迭代器）。

其实普通迭代器和const的区别就在operator*和operator->

而set的插入不需要修改：

pair<iterator, bool> insert(const K& k)
{return _t.insert(k);
}

return的时候会调用拷贝构造函数，也就是构造函数，把普通迭代器转化为const迭代器。

六、set源码

#pragma once
#include "RBTree.h"namespace yyh
{template <class K>class set{struct SetKeyOfT{const K& operator()(const K& k){return k;}};public:typedef typename RBTree<K, K, SetKeyOfT >::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT >::const_iterator const_iterator;iterator begin() const{return _t.begin();}iterator end() const{return _t.end();}pair<iterator, bool> insert(const K& k){return _t.insert(k);}private:RBTree<K, K, SetKeyOfT> _t;};
}

七、map源码

#pragma once
#include "RBTree.h"namespace yyh
{template <class K, class V>class map{struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapKeyOfT >::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT >::const_iterator \const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}pair<iterator, bool> insert(const const pair<K, V>& kv){return _t.insert(kv);}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};
}

八、红黑树源码

#pragma once
#include <iostream>
#include <cstdlib>
#include <cassert>
#include <string>using namespace std;enum Colour
{RED,BLACK,
};template <class T>
struct RBTreeNode
{RBTreeNode(const T& data): _data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;
};template <class T, class Ref, class Ptr>
struct RBTIterator
{typedef RBTreeNode<T> Node;typedef RBTIterator<T, Ref, Ptr> self;typedef RBTIterator<T, T&, T*> iterator;RBTIterator(const iterator& s): _node(s._node){}RBTIterator(Node* node): _node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const self& it){return _node != it._node;}bool operator==(const self& it){return _node == it._node;}self& operator++(){if (_node->_right){Node* min = _node->_right;while (min->_left){min = min->_left;}_node = min;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_right == cur){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}self& operator--(){if (_node->_left){Node* max = _node->_left;while (max && max->_right){max = max->_right;}_node = max;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_left == cur){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}Node* _node;
};template <class K, class T, class KeyOfT>
class RBTree
{
public:typedef RBTreeNode<T> Node;typedef RBTIterator<T, T&, T*> iterator;typedef RBTIterator<T, const T&, const T*> const_iterator;iterator begin(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}const_iterator begin() const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);}const_iterator end() const{return const_iterator(nullptr);}pair<iterator, bool> insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(iterator(_root), true);}KeyOfT kot;// 仿函数比较Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else return make_pair(iterator(cur), false);}cur = new Node(data);Node* newnode = cur;if (kot(data) < kot(parent->_data)){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){// 找g 与 uNode* g = parent->_parent;if (parent == g->_left){Node* u = g->_right;// 情况一 u存在且为红if (u && u->_col == RED){parent->_col = u->_col = BLACK;g->_col = RED;// 继续往上处理cur = g;parent = cur->_parent;}else // 情况二或情况三{if (cur == parent->_left)// 情况二{//   g//  p// cRotateR(g);parent->_col = BLACK;g->_col = RED;}else// 情况三{//  g// p//  cRotateL(parent);RotateR(g);//   c// p   gcur->_col = BLACK;g->_col = RED;}break;}}else{Node* u = g->_left;// 情况一if (u && u->_col == RED){u->_col = parent->_col = BLACK;g->_col = RED;cur = g;parent = cur->_parent;}else{// 情况二// g//  p//   cif (cur == parent->_right){RotateL(g);parent->_col = BLACK;g->_col = RED;}else// 情况三{// g//  p// cRotateR(parent);RotateL(g);cur->_col = BLACK;g->_col = RED;}break;}}}// 上面有可能把_root的颜色变为红_root->_col = BLACK;return make_pair(iterator(newnode), true);}void RotateL(Node* parent){Node* top = parent->_parent;Node* right = parent->_right;parent->_right = right->_left;if (right->_left) right->_left->_parent = parent;right->_left = parent;parent->_parent = right;if (top)// 子树{if (parent == top->_left) top->_left = right;else top->_right = right;right->_parent = top;}else// 完整的树{_root = right;_root->_parent = nullptr;}}void RotateR(Node* parent){Node* top = parent->_parent;Node* left = parent->_left;Node* leftR = left->_right;parent->_left = leftR;if (leftR) leftR->_parent = parent;left->_right = parent;parent->_parent = left;if (top){if (parent == top->_left) top->_left = left;else top->_right = left;left->_parent = top;}else{_root = left;_root->_parent = nullptr;}}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << "<=>" << root->_kv.second << endl;_Inorder(root->_right);}void Inorder(){_Inorder(_root);}bool _IsBalance(Node* root, int i, int flag){if (root == nullptr){if (i != flag){cout << "errno: 左右子树黑色节点数目不同" << endl;return false;}return true;}// 红节点时判断父亲if (root->_col == RED){if (root->_parent->_col == RED){cout << "errno: 红-红" << endl;return false;}}if (root->_col == BLACK){i++;}return _IsBalance(root->_left, i, flag) && _IsBalance(root->_right, i, flag);}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}// 找标准值Node* cur = _root;int flag = 0;while (cur){if (cur->_col == BLACK){flag++;}cur = cur->_left;}int i = 0;return _IsBalance(_root, i, flag);}private:Node* _root = nullptr;
};

http://www.ppmy.cn/news/28595.html

相关文章

JAVA中 throw 和 throws 的区别含案例

JAVA中 throw 和 throws 的区别含案例

JAVA中 throw 和 throws 的区别含案例 在 Java 中&#xff0c;throw 和 throws 是两个关键字&#xff0c;它们用于处理异常。 throw 关键字用于抛出一个异常对象。一旦抛出异常&#xff0c;程序将停止执行当前方法的剩余代码&#xff0c;并尝试寻找与该异常匹配的 catch 块来…
阅读更多...
Java反射系列--方法大全

Java反射系列--方法大全

原文网址&#xff1a;Java反射系列--方法大全_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Java反射相关的方法。 Class相关方法 方法 说明 getName() 返回String形式的该类的名称。 newInstance() 根据某个Class对象产生其对应类的实例&#xff0c;它调用的是此类的默认构…
阅读更多...
【手撕面试题】JavaScript（高频知识点二）

【手撕面试题】JavaScript（高频知识点二）

目录 面试官&#xff1a;请你谈谈JS的this指向问题 面试官&#xff1a;说一说call apply bind的作用和区别&#xff1f; 面试官&#xff1a;请你谈谈对事件委托的理解 面试官&#xff1a;说一说promise是什么与使用方法&#xff1f; 面试官&#xff1a;说一说跨域是什么&a…
阅读更多...
【笔记】C# 数据类型转换

【笔记】C# 数据类型转换

文章目录前言类型转换的概念1&#xff0c;隐式转换2&#xff0c;显式转换3&#xff0c;程序类转换结语前言 &#x1f33b; 大家好啊&#xff0c;我是writer桑&#xff0c;本章是关于 C# 数据类型转换的一个总结&#xff0c;其中包含隐式、显示转换和程序类转换&#xff0c;方便…
阅读更多...
微服务框架-学习笔记

微服务框架-学习笔记

1 微服务架构介绍 1.1 系统架构演变历史 单体架构垂直应用架构&#xff1a;按照业务线垂直划分分布式架构&#xff1a;抽出业务无关的公共模块SOA架构&#xff1a;面向服务微服务架构&#xff1a;彻底的服务化1.2 微服务架构概览 1.3 微服务架构核心要素 服务治理&#xff1…
阅读更多...
Benchmark测试——fio——源码分析

Benchmark测试——fio——源码分析

1. main 1.1 parse_options() 解析选项&#xff0c;更新数据结构 1.1.1 fio_init_options() 1.1.2 fio_test_cconv(&def_thread.o) <cconv.c> 1.1.2.1 convert_thread_options_to_cpu() 传递options给数据结构 1.1.3 parse_cmd_line() switch语句多路选择&am…
阅读更多...
mysql数据库之索引

mysql数据库之索引

索引概念 mysql索引的概念 1、索引是一个排序的列表&#xff0c;在这个列表中存储着索引的值和包含这个值的数据所在行的物理地址&#xff08;类似于c语言的链表通过指针指向数据记录的内存地址&#xff09;。 2、使用索引后可以不用扫描全表来定位某行的数据&#xff0c;而是…
阅读更多...
计算结构体大小

计算结构体大小

计算结构体大小 目录计算结构体大小一. 结构体内存对齐1. 简介2. 嵌套结构体二. offsetof三. 内存对齐的意义四. 修改默认对齐数一. 结构体内存对齐 以字节&#xff08;bety&#xff09;为单位 1. 简介 对于结构体成员在内存里的存储&#xff0c;存在结构体的对齐规则&#…
阅读更多...
最新文章

Copyright @ 2022~2023