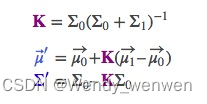原文:The alpha - beta - gamma filter (kalmanfilter.net)
一维卡尔曼滤波
在本章中,我们将在一个维度上推导出卡尔曼滤波。本章的主要目标是简单直观地解释卡尔曼滤波的概念,而不使用可能看起来复杂和令人困惑的数学工具。
我们将逐步推进卡尔曼滤波方程。
在本章中,我们推导出没有过程噪声的卡尔曼滤波方程。在下一章中,我们将添加过程噪声。
无过程噪声的一维卡尔曼滤波
正如我前面提到的,卡尔曼滤波器基于五个方程。我们已经熟悉其中的两个:
- 状态更新公式
- 动态模型方程
在本章中,我们推导出另外三个卡尔曼滤波方程并修正状态更新方程。
与 滤波器一样,卡尔曼滤波器采用“测量、更新、预测”算法。
与 滤波器相反,卡尔曼滤波器将测量值、当前状态估计和下一个状态估计(预测)视为正态分布的随机变量。随机变量由均值和方差描述。
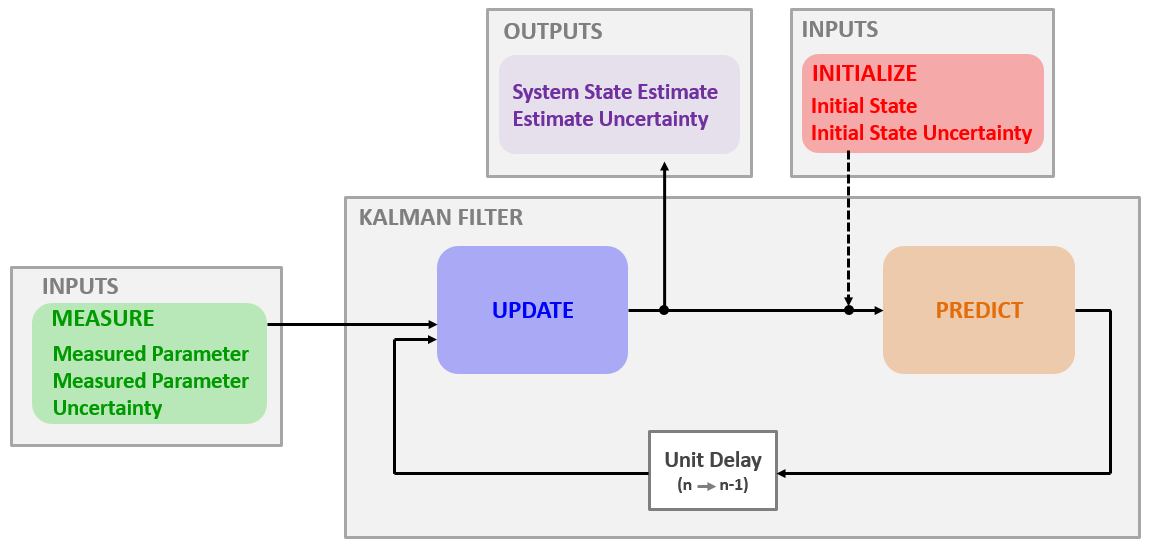
下图提供了卡尔曼滤波算法的低级示意图描述:
让我们回顾一下我们的第一个示例(金条重量测量);我们进行了多次测量,并通过平均计算了估计值。
我们得到了以下结果:
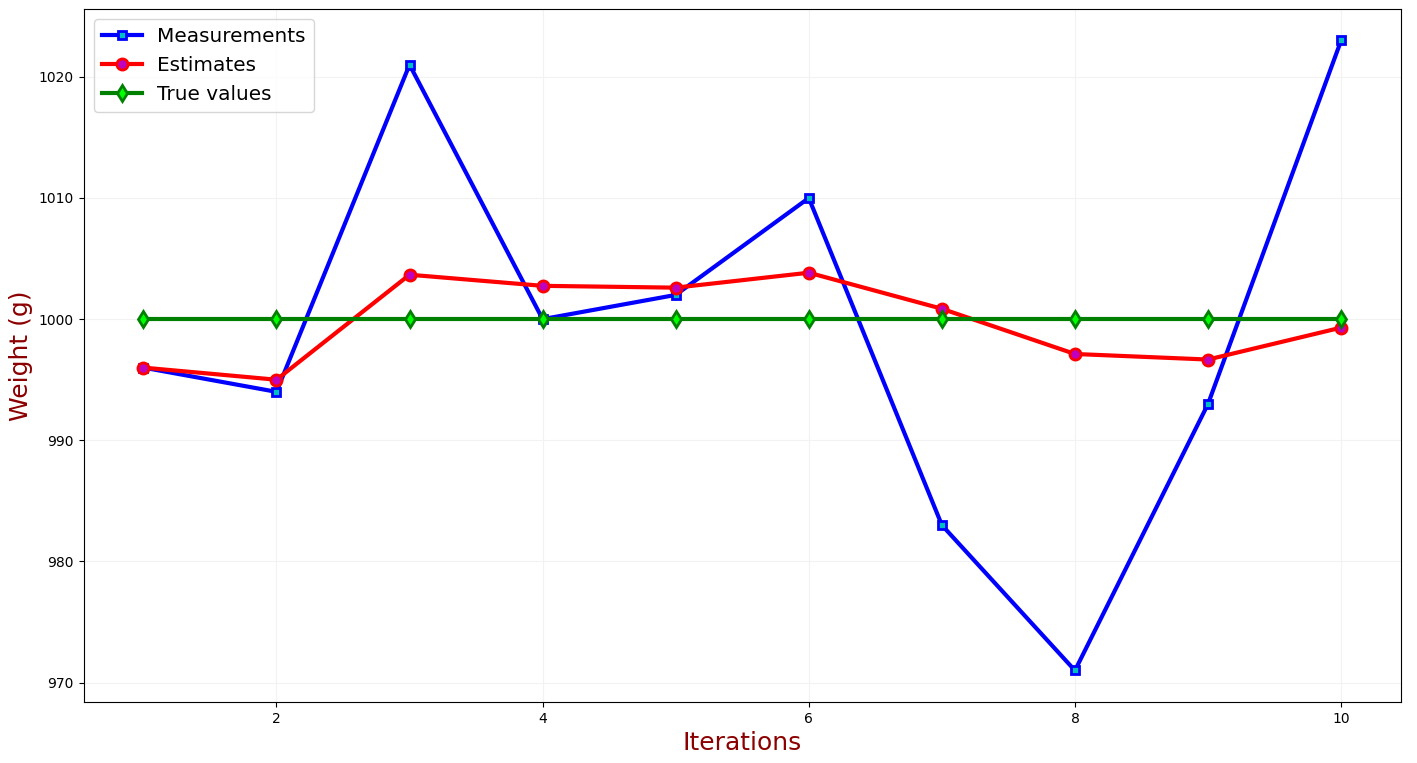
上图显示了真实值、测量值和估计值与测量次数的关系。
估计为随机变量
估计值(红线)和真值(绿线)之间的差值是估计误差。如您所见,当我们进行额外的测量时,估计误差会变小,并且它收敛于零,而估计值收敛于真实值。我们不知道估计误差,但我们可以估计状态不确定性。
我们用 p 表示状态估计方差。
作为随机变量进行测量
测量误差是测量值(蓝色样本)和真实值(绿线)之间的差异。由于测量误差是随机的,我们可以通过方差来描述它们。测量误差的标准偏差 (
) 是测量误差是测量值(蓝色样本)和真实值(绿线)之间的差异。
注意:在一些文献中,测量不确定度也称为测量误差。
我们用 r 表示测量方差。
测量误差的方差可以由测量设备供应商提供,计算或通过校准程序凭经验得出。
例如,在使用秤时,我们可以通过对具有已知重量的物品进行多次测量来校准秤,并根据经验得出标准偏差。秤供应商还可以提供测量不确定度参数。
对于雷达等高级传感器,测量不确定度取决于几个参数,如SNR(信噪比)、波束宽度、带宽、目标时间、时钟稳定性等。每个雷达测量都有不同的SNR、波束宽度和目标时间。因此,雷达计算每次测量的不确定性并将其报告给跟踪器。
让我们看一下权重测量PDF(概率密度函数)。
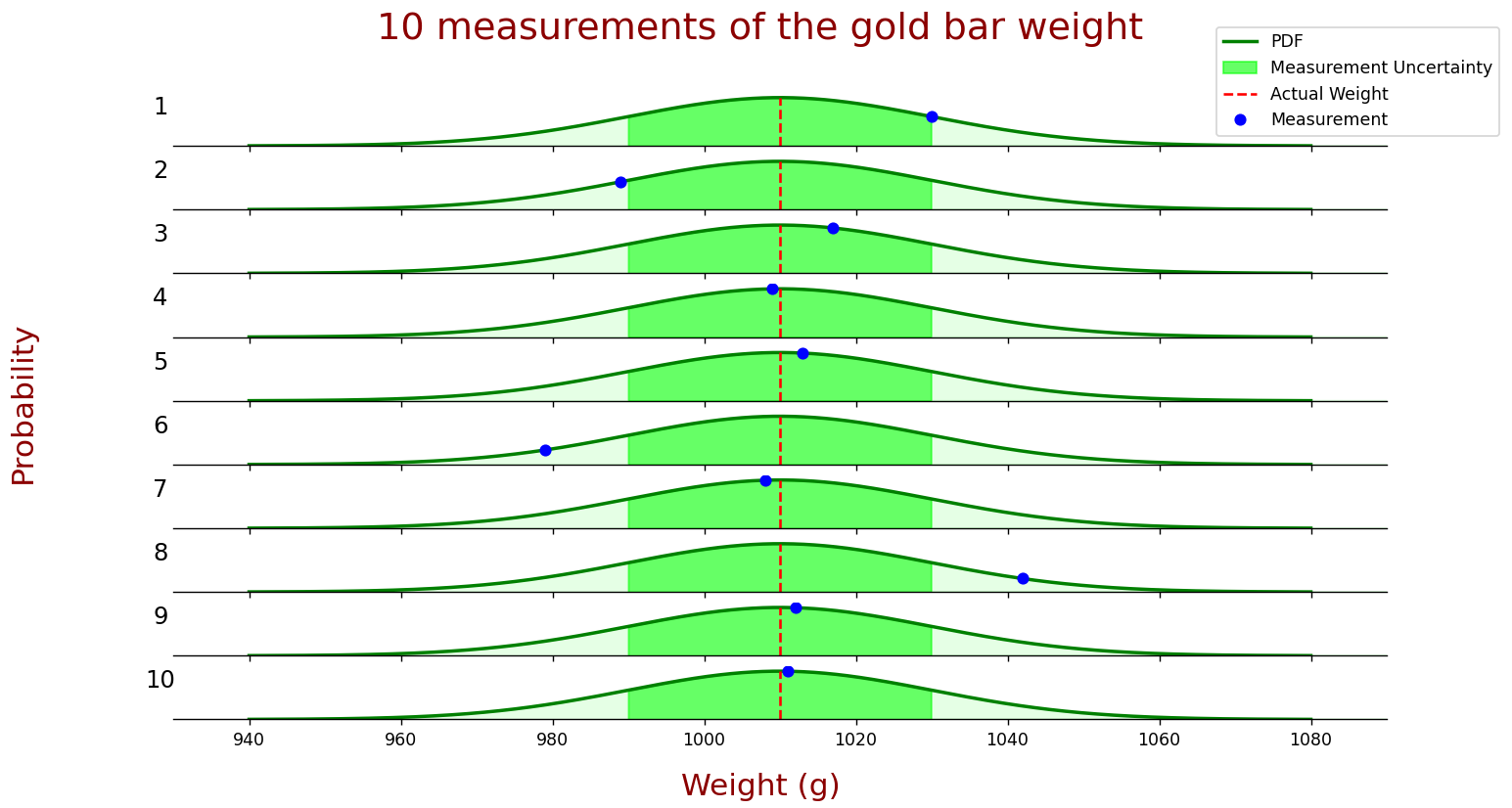
下图显示了金条重量的十个测量值。
- 蓝色圆圈描述测量值。
- 真实值由红色虚线描述。
- 绿线描述了测量的概率密度函数。
- 绿色粗体区域是测量的标准偏差(
),即测量值位于该区域内的概率为 68.26%。
如您所见,7 个测量值中有 10 个在 1 边界内。
状态预测
在我们的第一个例子中,金条重量的测量,动态模型是恒定的:
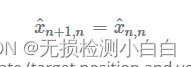
在第二个例子中,一维雷达案例,我们使用运动方程将当前状态(目标位置和速度)外推到下一个状态:
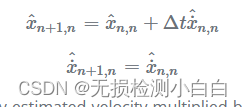
即,预测位置等于当前估计位置加上当前估计速度乘以时间。预测速度等于当前速度估计值(假设速度模型恒定)。
动态模型方程取决于系统。
由于卡尔曼滤波将估计值视为随机变量,我们还必须将估计方差 外推到下一个状态。
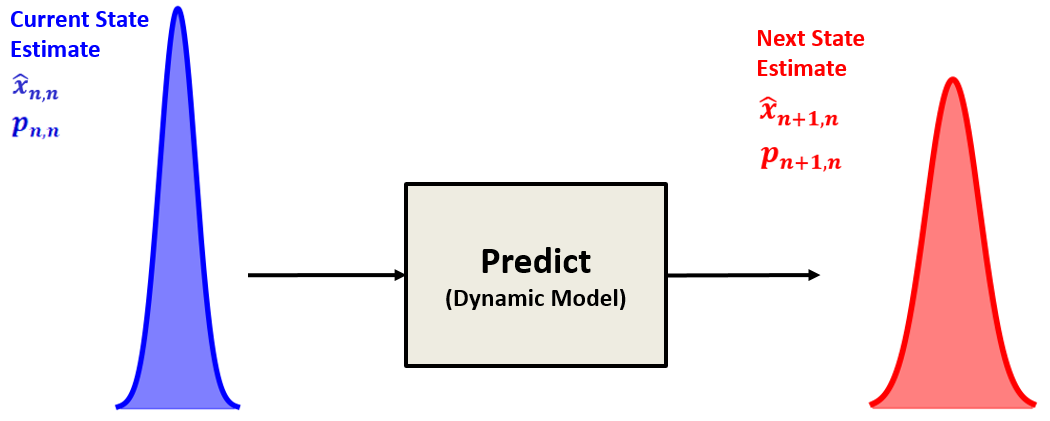
在我们的第一个示例(金条重量测量)中,系统的动态模型是恒定的。因此,估计不确定性外推为:
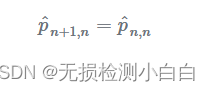
其中:
p 是金条权重的估计方差。
在第二个示例中,估计不确定性外推为:

其中:
| 是位置估计方差 | |
| 是速度估计方差 |
即,预测位置估计方差等于当前位置估计方差加上当前速度估计方差乘以时间平方。预测的速度估计方差等于当前速度估计方差(假设速度模型恒定)。
请注意,对于方差为 的任何正态分布随机变量 x , kx 呈正态分布,方差为
,因此不确定性外推方程中的时间项是平方的。您可以在请注意,对于任何正态分布的随机变量中找到详细说明。
估计不确定性外推方程称为协方差外推方程,它是第三个卡尔曼滤波方程。为什么是协方差?我们将在多元卡尔曼滤波章节中看到这一点。
状态更新
为了估计系统的当前状态,我们组合了两个随机变量:
- 先前状态估计(在先前状态预测的当前状态估计)
- 测量
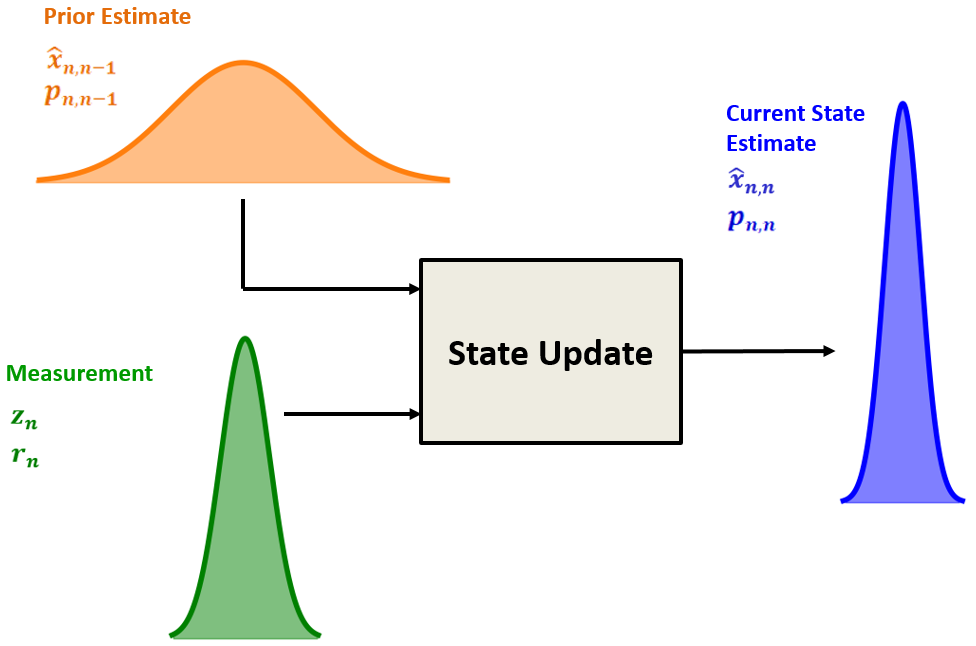
卡尔曼滤波是最佳滤波。它将先前的状态估计与测量相结合,以最小化当前状态估计的不确定性。
当前状态估计值是测量值和先前状态估计值的加权平均值:

其中 和
是测量值和先验状态估计值的权重。
我们可以写 如下:

方差之间的关系由下式给出:

其中:
是最优组合估计的方差
是先验估计值的方差
是测量值的方差
请记住,对于方差为 的任何正态分布随机变量 x, kx 呈正态分布,方差为
。您可以在请记住,对于任何正态分布的随机变量中找到详细说明。
由于我们正在寻找最佳估计,因此我们希望最小化。
为了找到最小化的
,我们将
与
进行区分并将结果设置为零。

因此

让我们将结果代入当前状态估计:
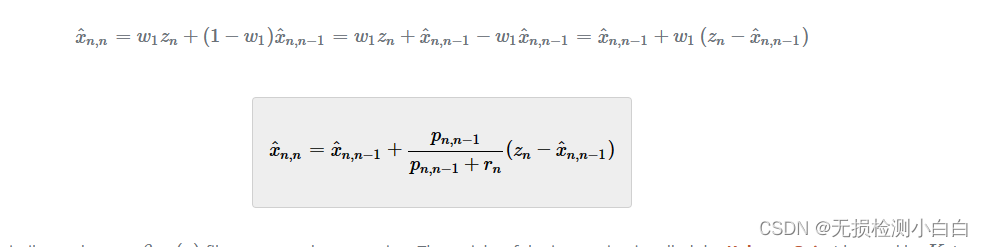
我们推导出了一个类似于 过滤器状态更新方程的方程。创新的权重称为我们推导出了一个方程,它看起来类似于(用
表示)。
卡尔曼增益方程是第四个卡尔曼滤波方程。在一个维度上,卡尔曼增益方程如下:
 其中:
其中:
| 是外推估计方差 | |
| 是测量方差 |
卡尔曼增益是一个介于 0 和 1 之间的数字:

最后,我们需要找到当前状态估计的方差。我们已经看到方差之间的关系由下式给出:

权重 是卡尔曼增益:

让我们找到 ( ) 项:
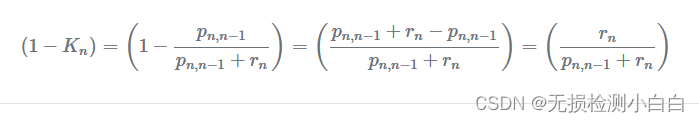
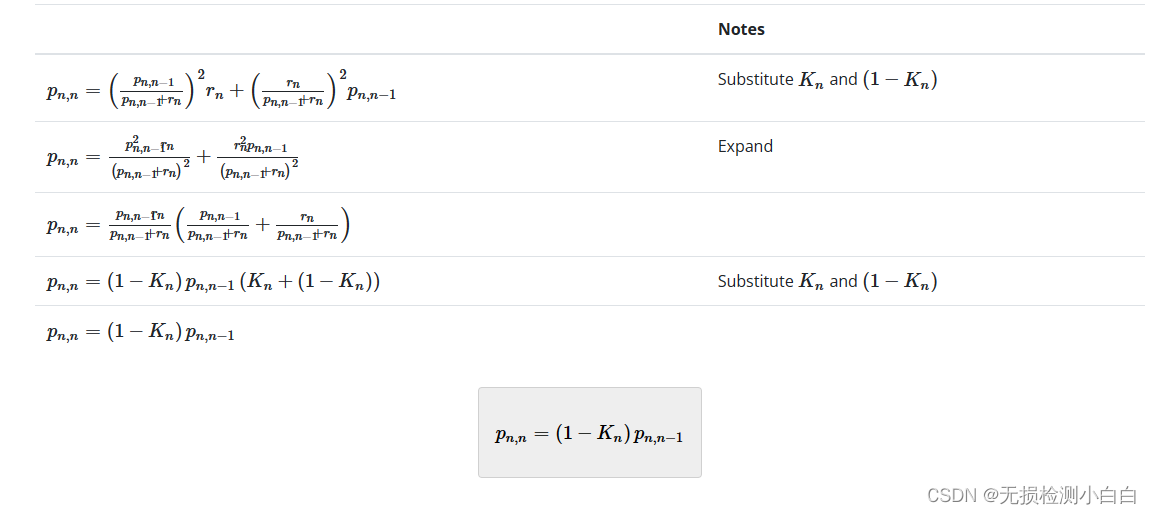
此公式更新当前状态的估计方差。它称为协方差更新方程。
从方程中可以清楚地看出,估计不确定性随着每次滤波器迭代而不断减小,因为 ( )。当测量不确定度较高时,卡尔曼增益较低。因此,估计不确定性的收敛将是缓慢的。然而,当测量不确定度较低时,卡尔曼增益很高。因此,估计不确定性将很快收敛到零。
因此,由我们决定进行多少次测量。如果我们测量建筑物的高度,并且我们对 3 厘米的精度感兴趣 ( ),我们应该进行测量,直到状态估计方差 (
) 小于
。
把所有东西放在一起
本节将所有这些部分合并到一个算法中。
过滤器输入为:
- 初始化
- 初始化仅执行一次,它提供两个参数:
- 初始系统状态 (
)
- 初始状态方差 (
)
- 初始系统状态 (
- 初始化参数可以由另一个系统、另一个过程(例如,雷达中的搜索过程)或基于经验或理论知识的有根据的猜测提供。即使初始化参数不精确,卡尔曼滤波器也可以收敛到接近真实值。
- 测量
- 测量针对每个过滤器周期执行,并提供两个参数:
- 测量的系统状态 (
)
- 测量方差 (
)
- 测量的系统状态 (
滤波器输出为:
- 系统状态估计 (
)
- 估计方差 (
)
下表总结了五个卡尔曼滤波方程。
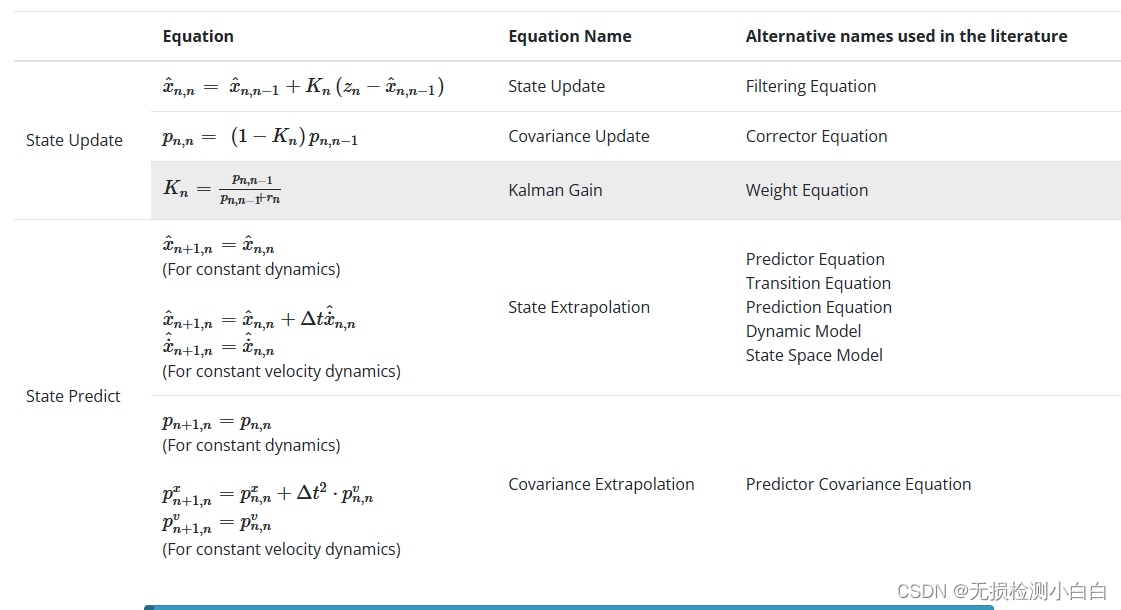
注1:上述公式不包括过程噪声。在下一章中,我们将添加过程噪声。
注2:状态外推方程和协方差外推方程取决于系统动力学。
注3:上表展示了针对特定情况量身定制的卡尔曼滤波方程的一种特殊形式。方程的一般形式稍后以矩阵表示法的形式呈现。现在,我们的目标是理解卡尔曼滤波器的概念。
下图提供了卡尔曼滤波器框图的详细说明。
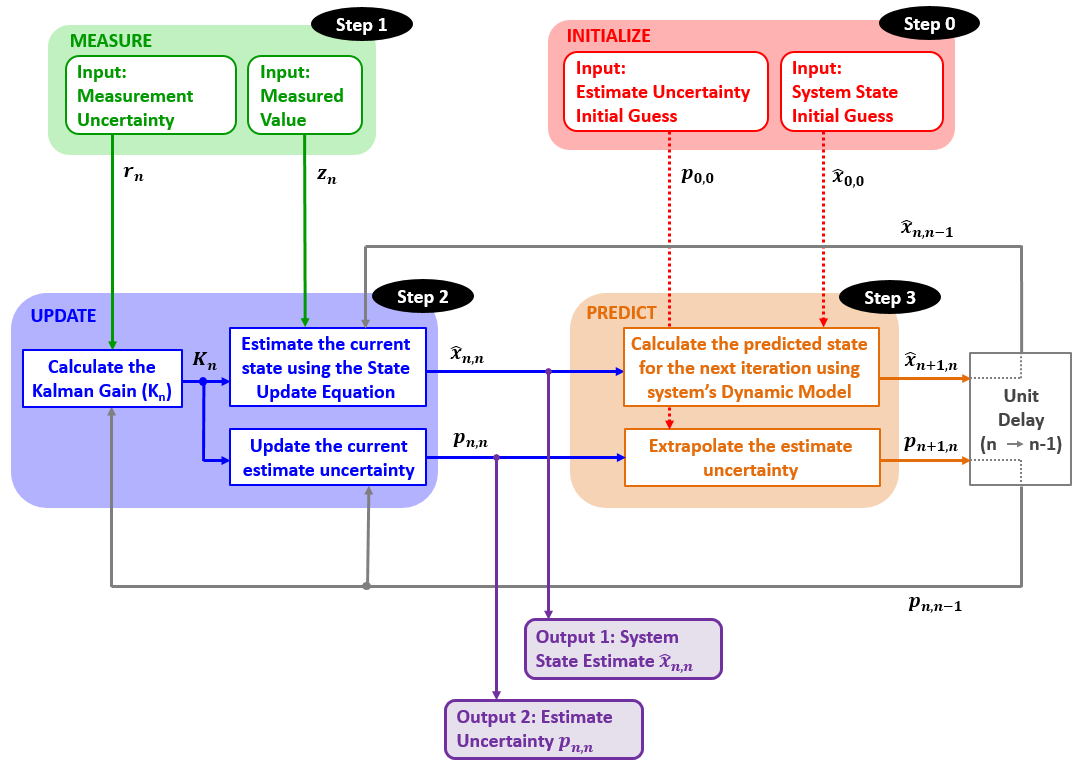
- 步骤 0:初始化
- 如上所述,初始化只执行一次,它提供了两个参数:
- 初始系统状态 (
)
- 初始状态方差 (
)
- 初始化后是预测。
- 初始系统状态 (
- 第 1 步:测量
- 测量过程提供两个参数:
- 测量的系统状态 (
)
- 测量方差 (
)
- 测量的系统状态 (
- 第 2 步:状态更新
- 状态更新过程负责系统当前状态的状态估计。
- 状态更新过程输入包括:
- 测量值 (
)
- 测量方差 (
)
- 先前预测的系统状态估计 (
)
- 先前预测的系统状态估计方差 (
)
- 根据输入,状态更新过程计算卡尔曼增益并提供两个输出:
- 当前系统状态估计 (
)
- 当前状态估计方差 (
)
- 这些参数是卡尔曼滤波输出。
- 测量值 (
- 第 3 步:预测
-
预测过程根据系统的动态模型将当前系统状态估计值及其方差外推到下一个系统状态。
在第一次筛选器迭代中,初始化被视为“先前状态估计值和方差”。
预测输出在以下筛选器迭代中用作先前(预测)状态估计和方差。
卡尔曼增益直觉
让我们重写状态更新公式:
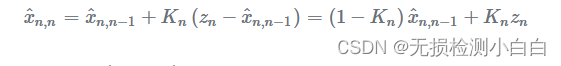
如您所见,卡尔曼增益 ( ) 是测量权重,(
) 项是当前状态估计值的权重。
当测量不确定度较高且估计不确定度较低时,卡尔曼增益接近于零。因此,我们对估计值给予很大的权重,对测量给予较小的权重。
另一方面,当测量不确定度较低且估计不确定度较高时,卡尔曼增益接近1。因此,我们对估计值给予较低的权重,对测量给予显着的权重。
如果测量不确定度等于估计不确定度,则卡尔曼增益等于 0.5。
卡尔曼增益 定义测量值的权重和形成新估计值时的先前估计值的权重。它告诉我们测量值对估计值有多大变化。
高卡尔曼增益
相对于估计不确定度的低测量不确定度将导致较高的卡尔曼增益(接近1)。因此,新的估计数将接近测量值。下图说明了高卡尔曼增益对飞机跟踪应用中估计值的影响。
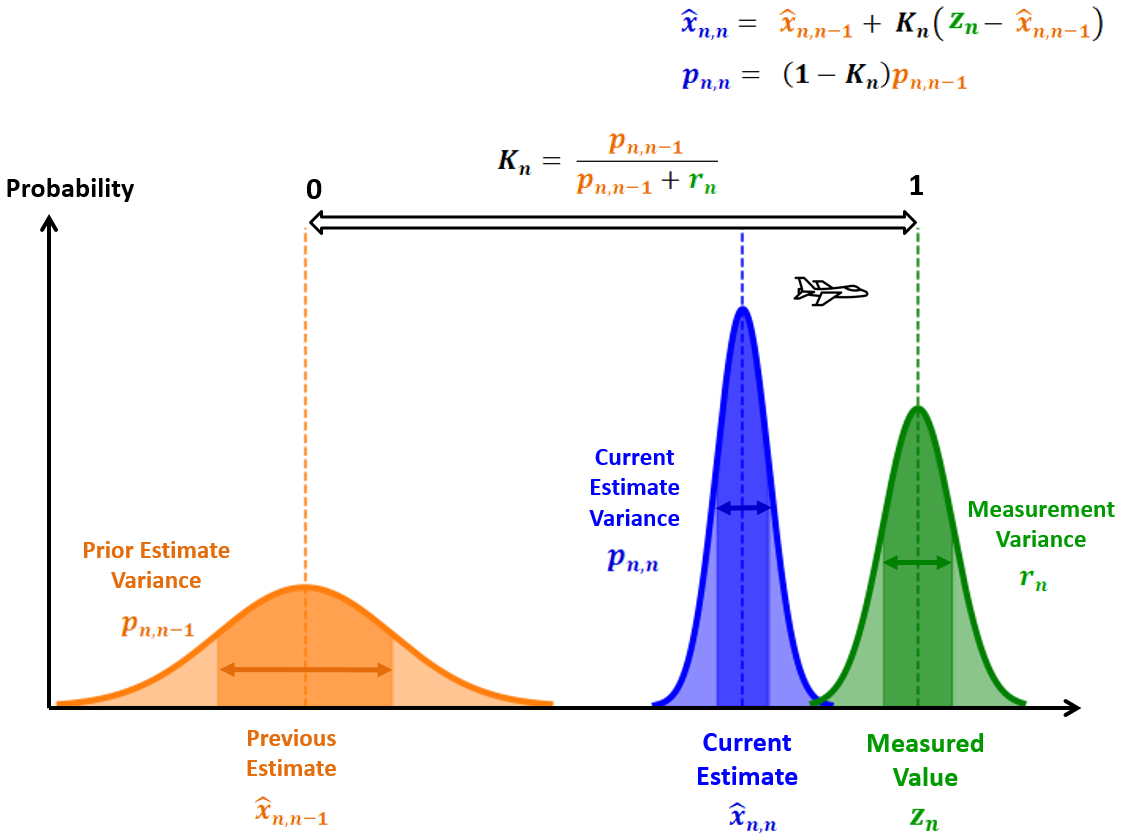
低卡尔曼增益
相对于估计不确定度较高的测量不确定度将导致较低的卡尔曼增益(接近0)。因此,新的估计数将接近先前的估计数。下图说明了低卡尔曼增益对飞机跟踪应用中估计值的影响。
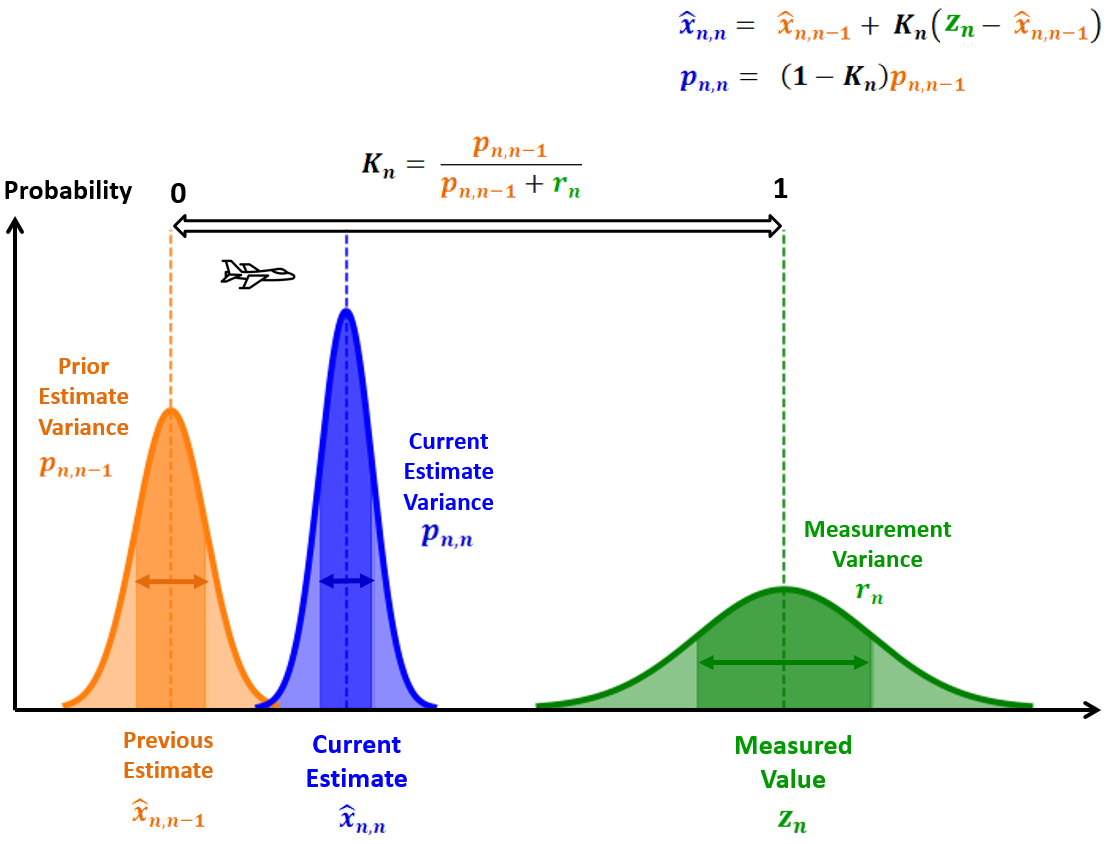
现在我们了解了卡尔曼滤波算法,并为第一个数值示例做好了准备。
示例 5 – 估计建筑物的高度
假设我们想使用不精确的高度计来估计建筑物的高度。
我们知道,建筑高度不会随时间而变化,至少在短测量过程中是这样。

数值示例
- 实际建筑高度为50米。
- 高度计测量误差(标准偏差)为 5 米。
- 这十个尺寸是:49.03米,48.44米,55.21米,49.98米,50.6米,52.61米,45.87米,42.64米,48.26米,55.84米。
迭代零
初始化
人们可以通过简单地观察来估计建筑物的高度。
用于初始化目的的建筑物的估计高度为:

现在我们将初始化估计方差。人类估计误差(标准差)约为 15 米:。因此方差为 225:
。

预测
现在,我们将根据初始化值预测下一个状态。
由于我们系统的动态模型是恒定的,即建筑物不会改变其高度:

外推估计方差也不会改变:

第一次迭代
步骤 1 - 测量
第一个测量值是:。
由于高度计测量误差的标准差 ( ) 为 5,因此方差 (
) 为 25,因此,测量方差为 : (
) 。
步骤 2 - 更新
卡尔曼增益计算:

估计当前状态:
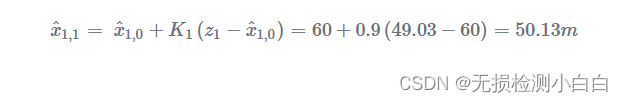
更新当前估计差异:
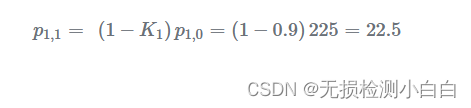
步骤 3 - 预测
由于我们系统的动态模型是恒定的,即建筑物不会改变其高度:

外推估计方差也不会改变:

第二次迭代
单位时间延迟后,上一次迭代的预测估计值将成为当前迭代中的先前估计值:

外推估计方差变为先验估计方差:

步骤 1 - 测量
第二个测量值为:
测量方差为:
步骤 2 - 更新
卡尔曼增益计算:
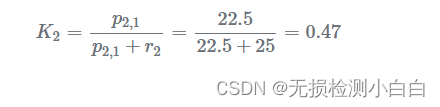
估计当前状态:
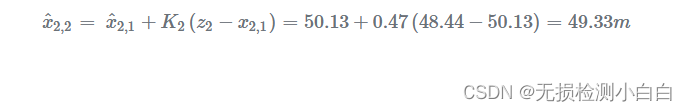
更新当前估计差异:
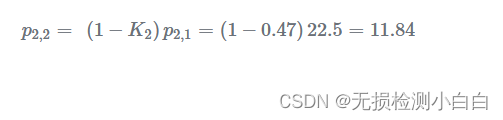
步骤 3 - 预测
由于我们系统的动态模型是恒定的,即建筑物不会改变其高度:

外推估计方差也不会改变:

迭代 3-10
下表汇总了后续迭代的计算:
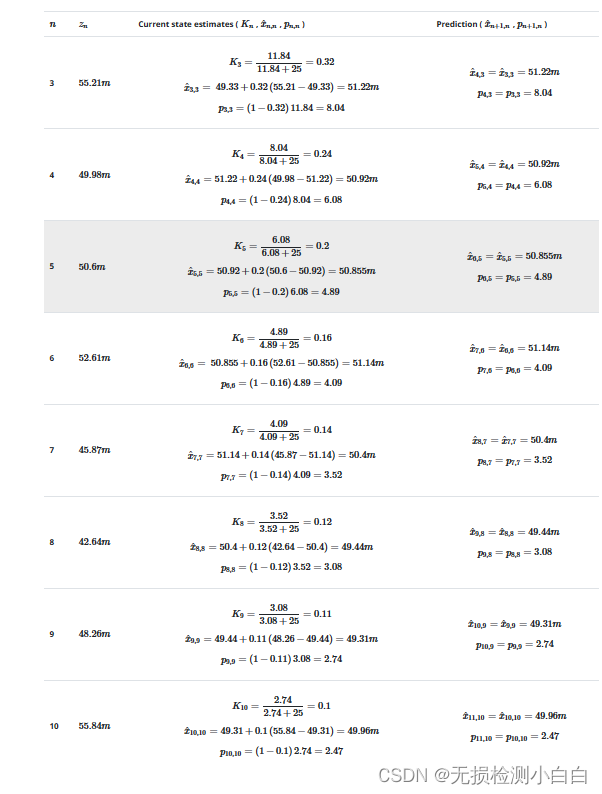
结果分析
首先,我们要确保卡尔曼滤波收敛。卡尔曼增益应逐渐减小,直到达到稳定状态。当卡尔曼增益较低时,噪声测量的权重也较低。下图描述了卡尔曼滤波器前一百次迭代的卡尔曼增益。
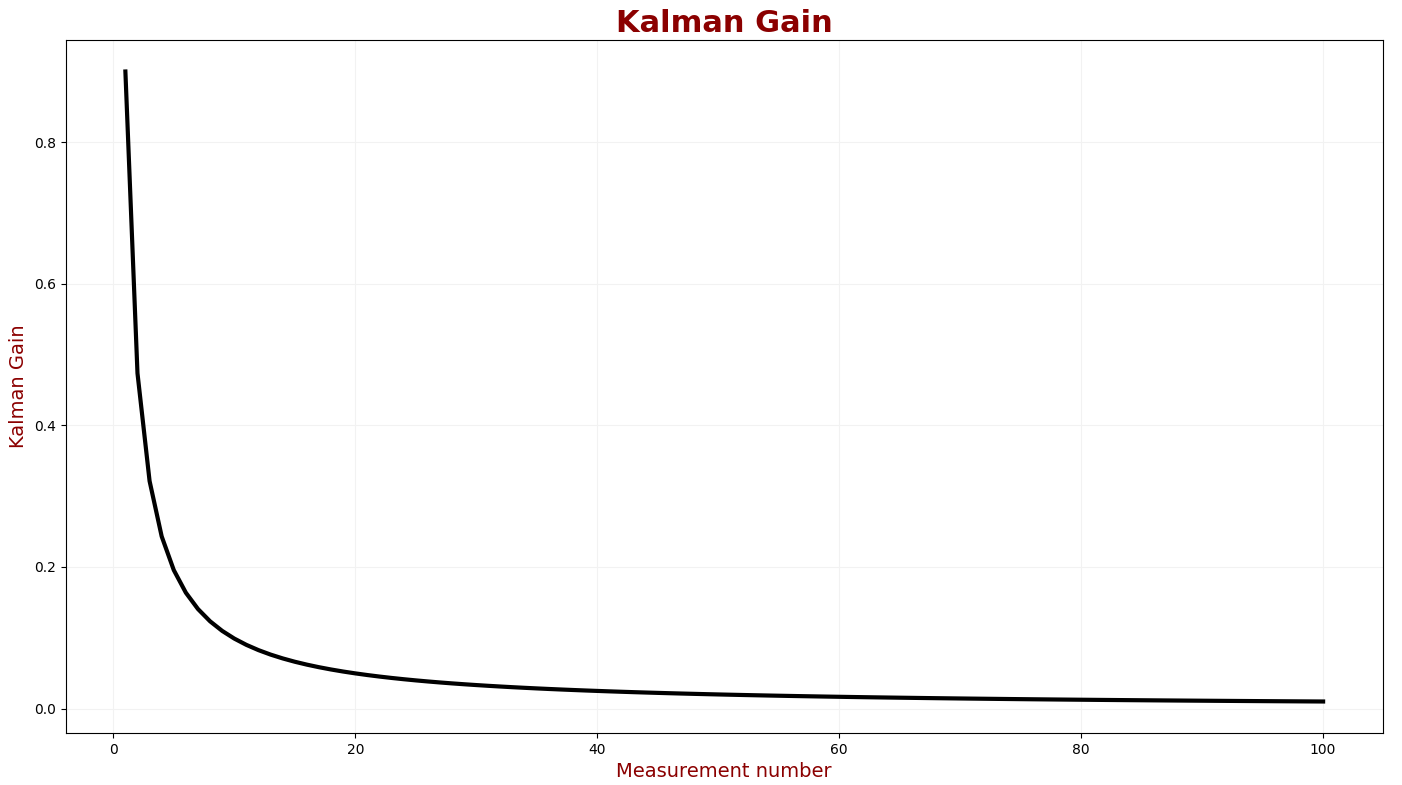
我们可以看到卡尔曼增益在前十次迭代中显着降低。卡尔曼增益在大约五十次迭代后进入稳定状态。
我们还想检查准确性。准确度表示测量值与真实值的接近程度。下图比较了前 50 次迭代的真实值、测量值和估计值。
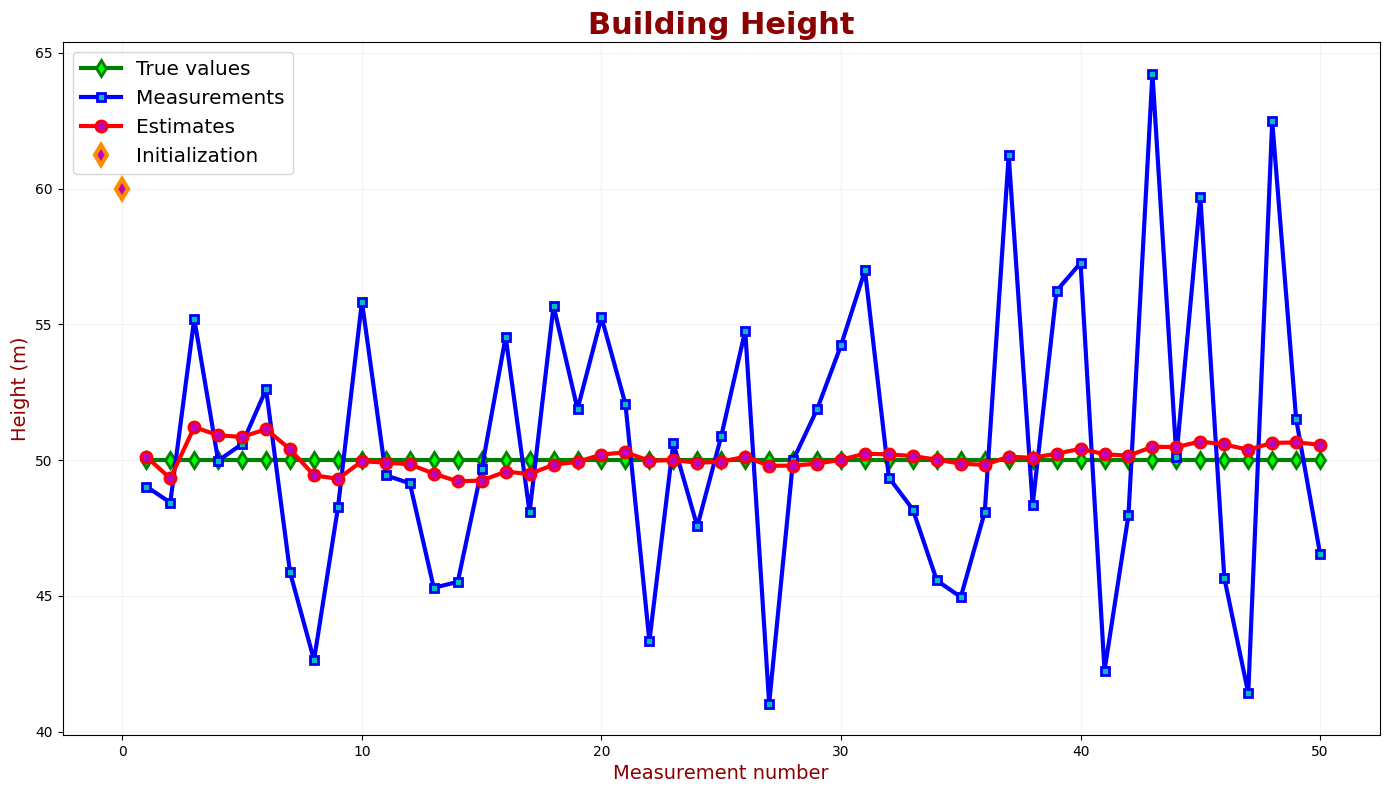
估计误差是真实值(绿线)和卡尔费休估计值(红线)之间的差异。我们可以看到,KF的估计误差在滤波器收敛区域减小。
可以根据特定的应用要求定义精度标准。典型的精度标准是:
- 最大误差
- 平均误差
- RMSE(均方根误差)
另一个重要参数是估计不确定性。我们希望钦哲基金会的估计是准确的;因此,我们对低估计不确定性感兴趣。
假设对于建筑物高度测量应用,需要 95% 的置信度。下图显示了 KF 估计值和具有 95% 置信区间的真实值。
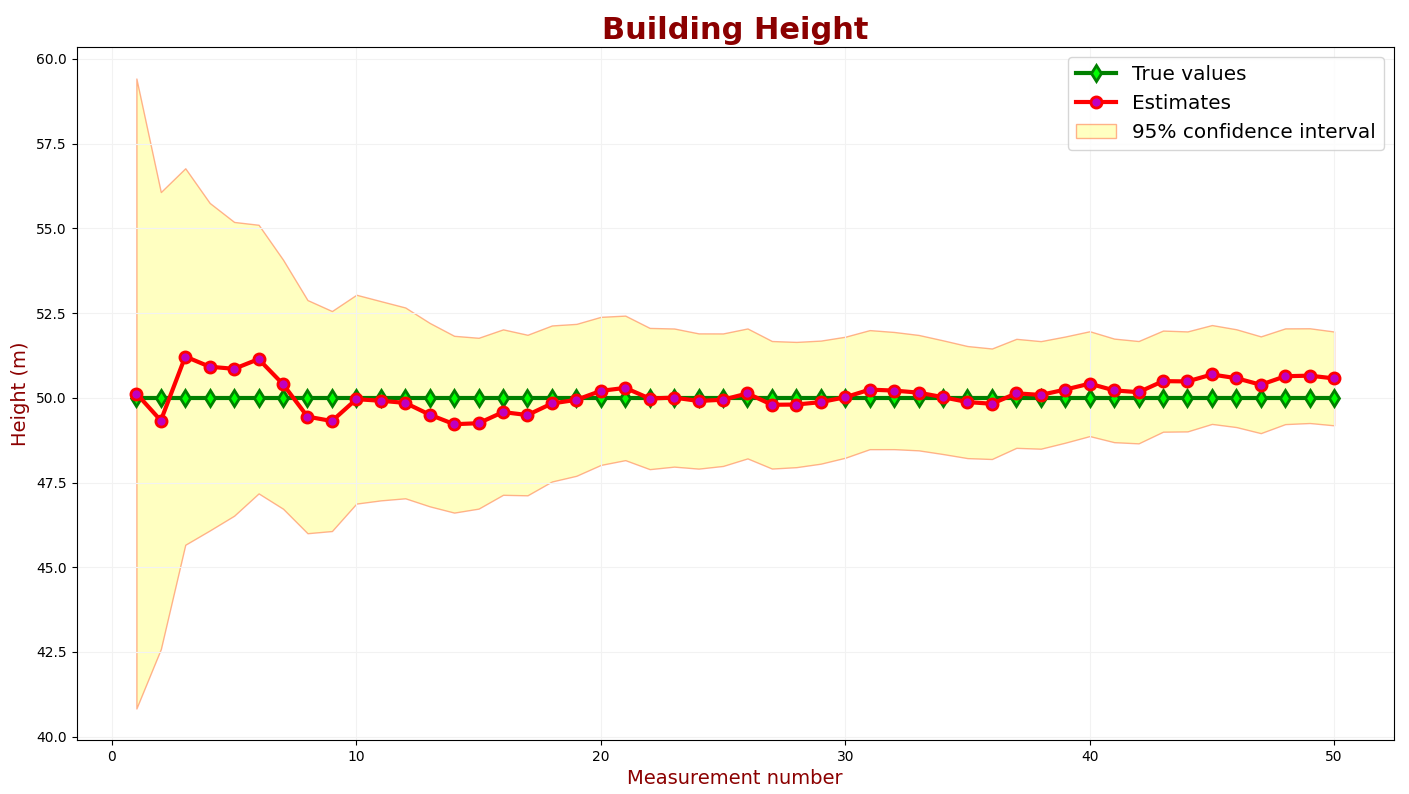
置信区间是根据估计值的不确定性计算的。您可以在此处找到置信区间计算的准则。
在上图中,置信区间被添加到估计值(红线)中。95% 的绿色样本应在 95% 置信区域内。
我们可以看到不确定性太高了。让我们降低测量不确定度。
下图描述了低测量不确定度参数的KF输出。
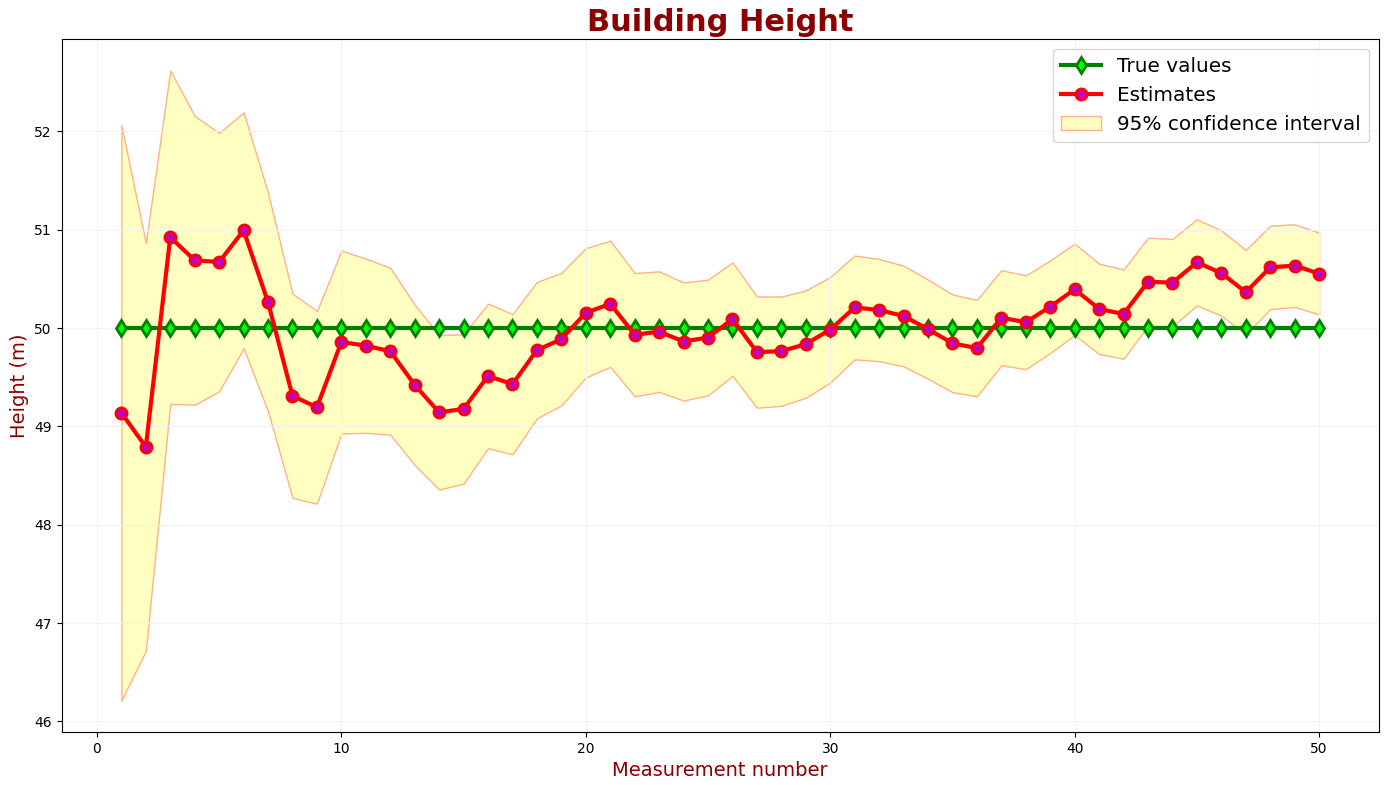
尽管我们降低了估计值的不确定性,但许多绿色样本都在 95% 置信区之外。卡尔曼滤波过于自信,对其准确性过于乐观。
让我们找到产生所需估计不确定度的测量不确定度。
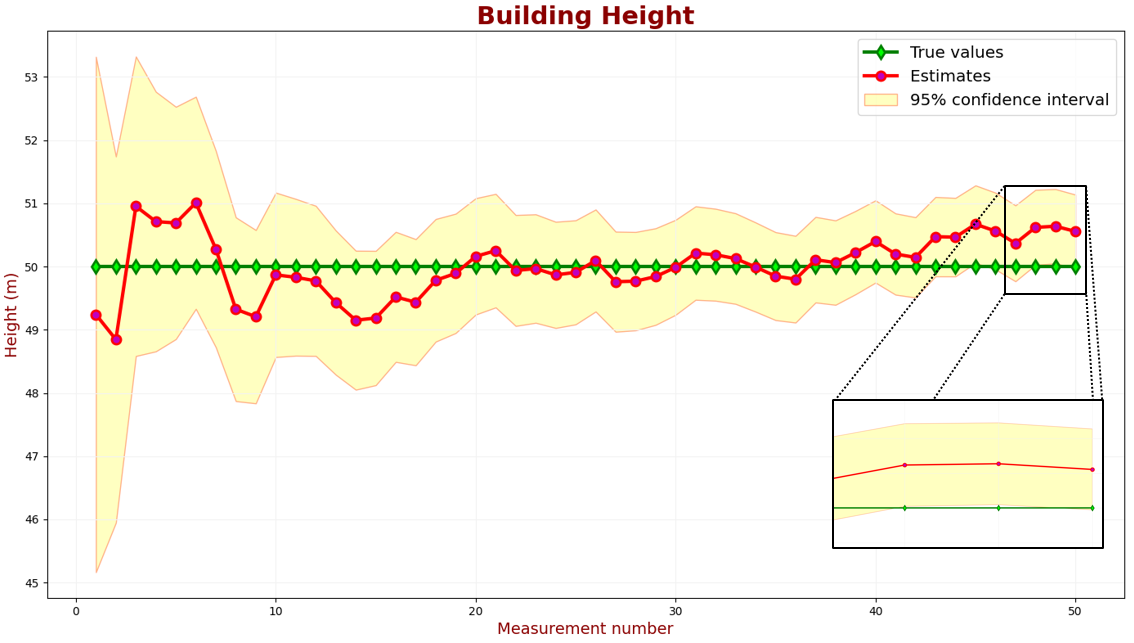
上图显示,2 个样本中有 50 个略高于 95% 置信区域。这种性能满足了我们的要求。
示例摘要
在本例中,我们使用一维卡尔曼滤波器测量了建筑高度。与 滤波器不同,卡尔曼增益是动态的,取决于测量设备的精度。
卡尔曼滤波使用的初始值并不精确。因此,状态更新方程中的测量权重较高,估计不确定度较高。
每次迭代时,测量重量都更低;因此,估计不确定性较低。
卡尔曼滤波输出包括估计值和估计不确定性。