题意
给定一个长度为 N N N 的数列,和 M M M 次询问,求出每一次询问的区间内数字的最大值。
对于 100 % 100\% 100% 的数据,满足 1 ≤ N ≤ 10 5 1\le N\le {10}^5 1≤N≤105, 1 ≤ M ≤ 2 × 10 6 1\le M\le 2\times{10}^6 1≤M≤2×106, a i ∈ [ 0 , 10 9 ] a_i\in[0,{10}^9] ai∈[0,109], 1 ≤ l i ≤ r i ≤ N 1\le l_i\le r_i\le N 1≤li≤ri≤N。
思路
什么是ST表
ST表,是一种用来处理**RMQ(区间最值问题)**的算法。ST表可以做到 O ( n log n ) \mathcal{O}(n\log{n}) O(nlogn) 预处理,之后 O ( 1 ) \mathcal{O}(1) O(1) 查询, ST表的空间复杂度也是 O ( n log n ) \mathcal{O}(n\log{n}) O(nlogn) 的。
如何实现ST表和它的原理
预处理
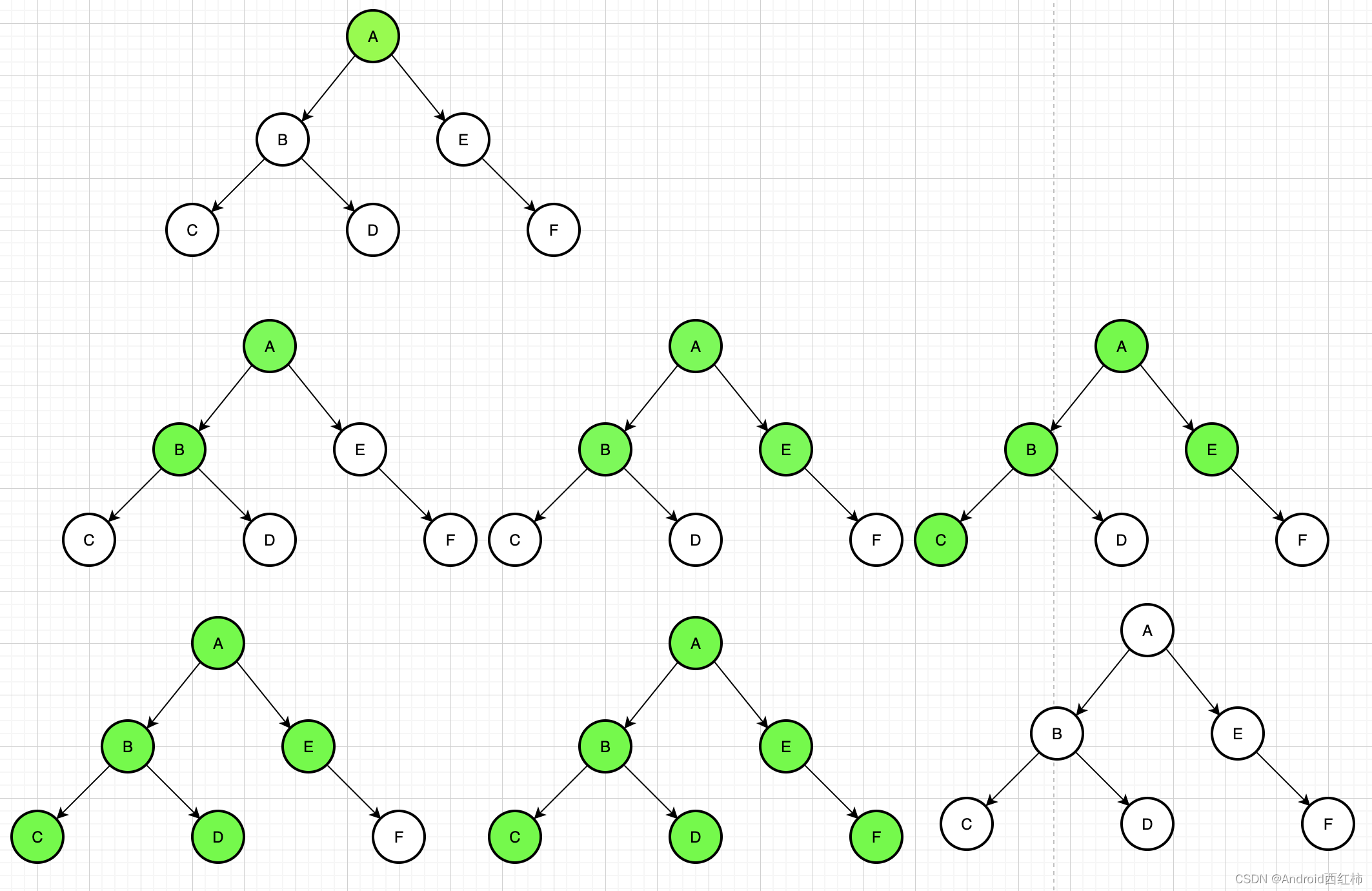
我们定义 S T i , j ST_{i,j} STi,j,为从第 i i i 个位置开始之后的 2 j 2^j 2j 个位置的区间最大值。 我们知道: 2 k = 2 k − 1 + 2 k − 1 2^k=2^{k-1}+2^{k-1} 2k=2k−1+2k−1,所以在预处理时也一样。ST表有些类似于dp的思想。 S T i , j = max ( S T i , j − 1 , S T i + 2 j − 1 , j − 1 ) ST_{i,j}=\max(ST_{i,j-1},ST_{i+2^{j-1},j-1}) STi,j=max(STi,j−1,STi+2j−1,j−1)
i , i + 1 , i + 2 , ⋯ , i + 2 j − 1 − 1 ⏟ max里的第一部分 , i + 2 j − 1 , i + 2 j − 1 + 1 , ⋯ , i + 2 j − 1 + 2 j − 1 − 1 ⏟ max里的第二部分 \underbrace{i,i+1,i+2,\cdots,i+2^{j-1}-1}_{\text{max里的第一部分}}\underbrace{,i+2^{j-1},i+2^{j-1}+1,\cdots,i+2^{j-1}+2^{j-1}-1}_{\text{max里的第二部分}} max里的第一部分 i,i+1,i+2,⋯,i+2j−1−1max里的第二部分 ,i+2j−1,i+2j−1+1,⋯,i+2j−1+2j−1−1
这样就可以从小合大了。
查询
查询的话也很简单,求一下 k = log ( r − l + 1 ) k= \log{(r-l+1)} k=log(r−l+1),也就是区间长度的覆盖。然后因为向下取整,不可以直接 S T l , k ST_{l,k} STl,k,而是要用 r − 2 k + 1 r-2^k+1 r−2k+1 重叠上去。不明白 r − 2 k + 1 r-2^k+1 r−2k+1的话就是从终点开始往中心走那么多格子,这样的话一定可以和 S T l , k ST_{l,k} STl,k 接上。
tips
需要注意一些边界,预处理的时候不要少处理,空间也要预留够。
代码
#include<cstdio>
#include <set>
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
typedef long long ll;
const ll MAXN=1e5+5;
ll st[MAXN][40];
ll query(ll l,ll r){ll k= ll(log2(r-l+1));return max(st[l][k],st[r-(1<<k)+1][k]);
}
ll n,m,l,r;
int main(){cin>>n>>m;for (int i = 1; i <=n ; ++i) {scanf("%lld",&st[i][0]);}for (int k = 1; k <=log2(MAXN) ; ++k) {for (int i = 1; i+(1<<k)-1<=n ; ++i) {st[i][k]= max(st[i][k-1],st[i+(1<<(k-1))][k-1]);}}for (int i = 1; i <=m ; ++i) {scanf("%lld%lld",&l,&r);printf("%lld\n", query(l,r));}return 0;
}