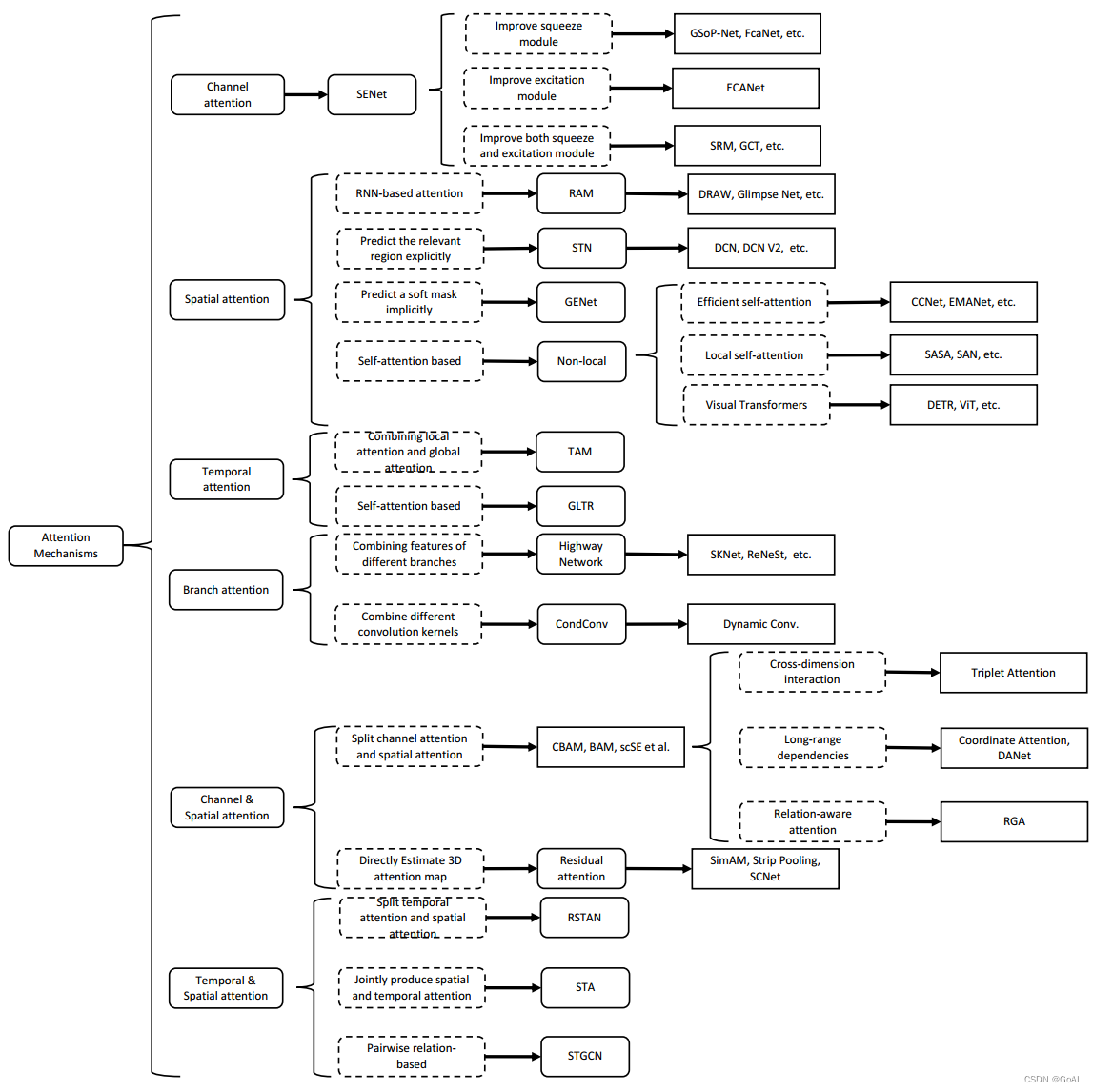
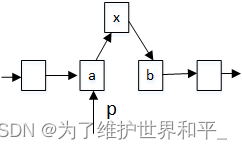
引言
什么是图嵌入?
我想从上节的deepwalk中已经有一个十分完整的轮廓了,这里引出deepwalk论文中的一张很形象的图(当然,上节的一些实战演练,也将这种嵌入关系进行了模拟与可视化,前文为:):
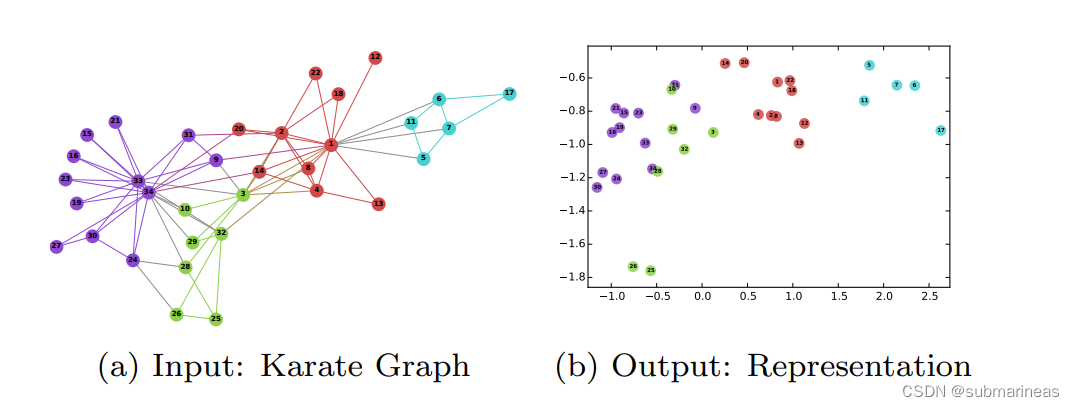
总的来说图嵌入技术大致可以分为两种:节点嵌入和图嵌入。当需要对节点进行分类,节点相似度预测,节点分布可视化时一般采用节点的嵌入;当需要在图级别(graph-level)上进行预测或者整个图结构越策,需要将整个图表示为一个向量进行嵌入表示。
图嵌入的好处以及坏处?
图嵌入的好处我认为是可以将图数据转换为低维向量,从而方便进行机器学习、数据挖掘、可视化等任务。图嵌入的坏处是可能会损失图的一些信息,如节点的属性、边的类型、子图的结构等。不同的图嵌入方法有不同的优缺点,需要根据具体的应用场景和需求来选择合适的方法。
以上一篇的deepwalk为例,它的随机游走方式如果是完全随机,那么会出现很多极端情况,比如它就往前迈一步,再回到原点,以及绕着一个方向不改变得走等等,而我们加了α\alphaα系数后,相当于给了一个向心力,让它能尽量以圆的方式运作,但也有坏处,就是更趋向于BFS,而不是DFS了。这里一个很形象的例子,就是数据结构中的链表,一个链表所代表的元素都是未知的,我们如果需要添加元素,那得遍历整条流程线,或者以头尾指针的方式才能达成需求,但随机游走里并没有安排指针,所以某种程度上,不具备泛化能力,过拟合程度比较高。
本节的另一种算法——Node2Vec,算是解决了deepwalk的一些缺点,可以看做是deepwalk的一种扩展,是结合了DFS和BFS随机游走的deepwalk。
Node2Vec
Node2Vec 介绍
DeepWalk可以说给大家带来了全新的思路,其意义远不止实验结果那么简单。理论上,对于任何图数据,或者是由关系型数据抽象出来的图数据,都可以利用DeepWalk得到Embedding,而且算法简单,易于扩展到大规模数据上;更为重要的,这启发了后续的研究者进行了更加深入的研究。
node2vec的作者针对DeepWalk不能用到带权图上的问题,提出了概率游走的策略,并使用AliasSampling进行采样,该算法在之后会尝试讲解,这里主要提及一下它的创新点。
在node2vec之前,deepwalk的游走是完全随机的,虽然也能获取到非常多的信息,但相对而言比较局部,包括deepwalk、line等算法,都是用中间词预测周围词的方式,缺少采样策略,于是node2vec提出了它的随机游走策略公式:
P(ci=x∣ci−1=v)={πvxZif (v,x)∈E0otherwise P\left(c_i=x \mid c_{i-1}=v\right)= \begin{cases}\frac{\pi_{v x}}{Z} & \text { if }(v, x) \in E \\ 0 & \text { otherwise }\end{cases}P(ci=x∣ci−1=v)={Zπvx0 if (v,x)∈E otherwise
给定一个起始节点 uuu,模拟随机游走的固定长度lll,上面为下一个节点 xxx 对于当前节点 vvv 的条件概率公式,其中,πvx{\pi_{v x}}πvx 是未归一化转移概率,ZZZ 是是归一化常数。
为了让随机游走能够反映网络的结构和特征,我们能产生相应的偏置(bias),来控制随机游走,这里引述了一下传统方法的不适用性,比如说最简单的偏置方法是根据边的权重来选择下一个节点,即边越重,选择该边连接概率越大,用 wvxw_{vx}wvx 代表当前节点 vvv 和 下一节点 xxx的权重,那么此时 wvx=πvxw_{vx}={\pi_{v x}}wvx=πvx ,但这种策略很显然太空洞与不切实际,所以加入了两个超参数 ppp 和 qqq 策略,来控制游走。假设当前随机游走经过边 (t,v)(t,v)(t,v) 到达顶点 vvv 设πvx=apq(t,v)⋅wv,x{\pi_{v x}}=a_{pq}(t,v)\cdot w_{v,x}πvx=apq(t,v)⋅wv,x,其中wvxw_{vx}wvx 一样是节点 vvv 和 下一节点 xxx的权重,那另一项系数可写为:
αpq(t,x)={1p=if dtx=01=if dtx=11q=if dtx=2\alpha_{p q}(t, x)=\left\{\begin{array}{ll} \frac{1}{p}= & \text { if } d_{t x}=0 \\ 1= & \text { if } d_{t x}=1 \\ \frac{1}{q}= & \text { if } d_{t x}=2 \end{array}\right.αpq(t,x)=⎩⎨⎧p1=1=q1= if dtx=0 if dtx=1 if dtx=2
dtxd_{tx}dtx 为 当前节点与下一节点的最短路径距离,这里论文中也解释了两个超参数的含义,qqq 为 In-out parameter ,ppp为 Return parameter ,跟单词表达的意思一样,即 ppp 控制重复访问刚刚访问过的顶点的概率,而 qqq 控制控向外还是向内走的概率,而上述公式中还有一个1,可以理解成不动,或者在当前节点徘徊。可能这有点抽象,所以论文中给出了一张图:

这就十分清晰了,这里可以举个例子,当 ppp 大 qqq 小时,属于DFS深度优先搜索,节点会朝 x2、x3x2、x3x2、x3等更远方前进,而反过来,则会朝来时的 ttt 回退,或者说BFS广度优先搜索,探索周围的区域。
那么到这里,是论文的创新点,将随机游走变成了一种概率游走的方式采样序列,并且对节点的采样也做了相应的优化,即AliasSampling算法。
AliasSampling算法(别名采样算法)
这里参考Alias Method:时间复杂度O(1)的离散采样方法 和 【数学】时间复杂度O(1)的离散采样算法—— Alias method/别名采样方法
首先我举个我认为还算比较贴切的例子,当然可能有点现实。包括我在内,其实对于彩票行业,都是充满了兴趣,每次买完都心生向往,即使过程中被一再剥削,在结果没有开出前都觉得心里有一块着落、期盼,幻想着鱼跃龙门,花开彼岸。因为彩票就是一张纸,一个号码,每个人都觉得权重都是一样的,都有中奖的机会,这就是等概率分布抽样,复杂度为O(1),但现实往往不是的,有些人位高权重,那自然能让自己的一亿分之一的概率变为十分之一以内,这里考虑多部门利益交互情况,所以,没有关系的普通人权重进一步被缩小,在没有黑手的情况下,全部人加起来可能也才十分之一,如果开奖的号码没有落入这十分之一,那可以说成两个集体,有权利的0.9,没有权的0.1,这就是二项分布抽样,复杂度也可看成是O(1)
上述英文原文中,用的例子我可以理解为红球、白球和篮球,每个有相应的概率,然后进行抽签,经典的古典概型问题。alias method就是把这两种方法结合起来。
假设,初始情况下球的概率分布为:

现在,缩放所有这些矩形,但我们不再使用最大值去进行归一化,而是按照1N\frac{1}{N}N1来均值归一化, 这里的例子是1/4变为1的概率,即为所有概率乘以N,为:

这时候再画条线,将前两个多余出来的部分填补到后两个框上,即:
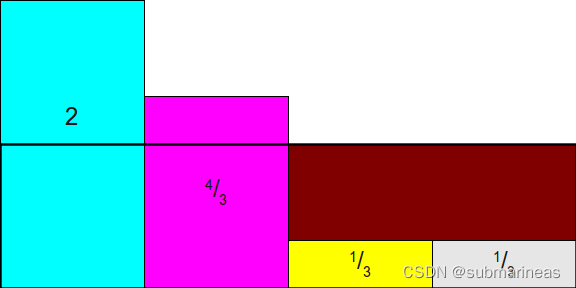
而这里需要注意的是,Alias Method一定要保证:每列中最多只放两个事件,即最终呈现的效果应该是这样的:

所以照着这种规则,就能将该算法拆成两部分,一部分是生成Alias Table,该table包括了上面的一系列预处理,另一部就是采样,产生两个随机数,具体步骤如下:
生成Alias Table的步骤是:
- 根据要求的概率分布计算累积分布,映射到[0,1]的线段上;
- 将N个事件的概率乘以N,得到一个新的概率数组q;
- 将q中小于1的元素放入一个队列smaller,将大于等于1的元素放入另一个队列larger;
- 从smaller中弹出一个元素i,从larger中弹出一个元素j;
- 在第i行第一列填入事件i,在第i行第二列填入事件j,在第j行第一列填入事件j;
- 将q[j]减去(1-q[i]),如果结果小于1,则将j放回smaller,否则将j放回larger;
- 重复步骤4-6,直到smaller或larger为空。
根据Alias Table采样的步骤是:
- 随机生成[1,N]之间的一个整数k,确定选中哪一行;
- 随机生成[0,1]之间的一个数p,根据概率判断是取样该行的第一列还是第二列;
- 如果p小于q[k],则输出该行第一列对应的事件;否则输出该行第二列对应的事件。
而上面我参考的知乎贴里,已经复现出来了该代码:
import numpy as np
def gen_prob_dist(N):p = np.random.randint(0,100,N)return p/np.sum(p)def create_alias_table(area_ratio):l = len(area_ratio)accept, alias = [0] * l, [0] * lsmall, large = [], []for i, prob in enumerate(area_ratio):if prob < 1.0:small.append(i)else:large.append(i)while small and large:small_idx, large_idx = small.pop(), large.pop()accept[small_idx] = area_ratio[small_idx]alias[small_idx] = large_idxarea_ratio[large_idx] = area_ratio[large_idx] - (1 - area_ratio[small_idx])if area_ratio[large_idx] < 1.0:small.append(large_idx)else:large.append(large_idx)while large:large_idx = large.pop()accept[large_idx] = 1while small:small_idx = small.pop()accept[small_idx] = 1return accept,aliasdef alias_sample(accept, alias):N = len(accept)i = int(np.random.random()*N)r = np.random.random()if r < accept[i]:return ielse:return alias[i]def simulate(N=100,k=10000,):truth = gen_prob_dist(N)area_ratio = truth*Naccept,alias = create_alias_table(area_ratio)ans = np.zeros(N)for _ in range(k):i = alias_sample(accept,alias)ans[i] += 1return ans/np.sum(ans),truthif __name__ == "__main__":alias_result,truth = simulate()
上面的步骤,我基本上就是对照着代码和参考文献里改写的,所以可以打印一下最后两个返回值,alias_result 即是分好类的Alias Table,而truth 即是原始值,即按最大值进行平均的全概率集合。
更详细的对于该种算法的存在性证明可以看参考中的推导。
Node2Vec算法详细步骤

其中PreprocessModifiedWeights是生成随机游走采样策略,然后生成随机游走序列,中间的node2vecWalk采样策略按照之前的全概率公式,即我上面所举的例子,14亿人买彩票,那时间复杂度是O(n)O(n)O(n),而用了AliaSample采样后,时间复杂度变为了O(1)O(1)O(1),具体原因在上一节,这里是用空间(预处理)换时间,适用于大量反复的抽样情况下,将离散分布抽样转化为均匀分布抽样。那么还是找个例子,我如果是个普通人,用该种采样策略,我的概率变了嘛?答案当然是没变,我依然是1/14亿,计算如下:

最开始的第二列的概率是1/3(1/2,1/3,1/12,1/12),然后改变了平均策略后,最终如上图,我的第二列概率为第二列本来的0.25 = 1/4,加上第一列被平均的1/3 * 1/4 = 1/12,最终结果依然是1/3,证必。
而根据随机(概率)游走策略后,即node2vecWalk,后面还有一部为 StochasticGradientDesc,论文中同样针对该优化策略进行了创新,引入了负采样的方式来减小计算量。
node2vec是一种图嵌入方法,它可以综合考虑深度优先搜索(DFS)邻域和广度优先搜索(BFS)邻域。它的优化目标是最大化每个节点与其采样邻居的相似度。
node2vec的目标函数是最大化给定一个节点uuu,其邻域节点集合NS(u)N_S(u)NS(u)出现的条件概率:
maxf∑u∈VlogPr(NS(u)∣f(u))\max_f \sum_{u \in V} \log Pr(N_S(u)|f(u))fmaxu∈V∑logPr(NS(u)∣f(u))
其中f(u)f(u)f(u)是将节点u映射为低维向量的函数,VVV是图中所有节点的集合,S是采样策略。
根据链式法则,上述条件概率可以分解为:
Pr(NS(u)∣f(u))=∏ni∈NS(u)Pr(ni∣f(u),n1,…,ni−1)Pr(N_S(u)|f(u)) = \prod_{n_i \in N_S(u)} Pr(n_i|f(u), n_1, …, n_{i-1})Pr(NS(u)∣f(u))=ni∈NS(u)∏Pr(ni∣f(u),n1,…,ni−1)
其中nin_ini是从节点uuu开始的随机游走中第iii个访问的节点。
为了简化计算,node2vec提出了条件独立性假设,每个nin_ini只依赖于前一个节点ni−1n_{i-1}ni−1,即:
Pr(ni∣f(u),n1,…,ni−1)≈Pr(ni∣f(ni−1))Pr(n_i|f(u), n_1, …, n_{i-1}) \approx Pr(n_i|f(n_{i-1}))Pr(ni∣f(u),n1,…,ni−1)≈Pr(ni∣f(ni−1))
这样就可以使用word2vec中的skip-gram模型来估计这个概率。然后第二种假设为特征空间对称性假设,一个顶点作为源顶点和作为近邻顶点的时候共享同一套embedding向量。具体地,对于每个源节点uuu和目标节点vvv,定义一个得分函数s(f(u),f(v))s(f(u), f(v))s(f(u),f(v))来衡量它们在特征空间中的相似度。通常使用点积作为得分函数:
s(f(u),f(v))=f(u)Tf(v)s(f(u), f(v)) = f(u)^T f(v)s(f(u),f(v))=f(u)Tf(v)
然后使用softmax函数将得分转换为概率:
Pr(ni=v∣f(ni−1)=u)=exp(s(f(u),f(v)))∑v’∈Vexp(s(f(u),f(v’)))Pr(n_i = v|f(n_{i-1}) = u) = \frac{\exp(s(f(u), f(v)))}{\sum_{v’ \in V} \exp(s(f(u), f(v’)))}Pr(ni=v∣f(ni−1)=u)=∑v’∈Vexp(s(f(u),f(v’)))exp(s(f(u),f(v)))
由于softmax函数涉及对所有可能的 vvv 求和,计算代价很高。因此node2vec采用了负采样技术来近似softmax。
负采样是一种提高训练速度并改善词向量质量的方法,它的思想是对每个正例(即真实存在于邻域中的节点对)采样 KKK 个负例(即随机选择不在邻域中的节点对),然后用二元逻辑回归来区分正例和负例,这其实只是更新一小部分权重,而不是所有权重。
具体地,对于每个正例(u,v)(u, v)(u,v),定义如下损失函数:
Jpos(u,v)=−log(σ(s(f(u),f(v))))−∑i=1KEvnPn(v)[log(σ(−s(f(u),f(vn))))]J_{pos}(u, v) = -\log(\sigma(s(f(u), f(v)))) - \sum_{i=1}^{K} E_{v_n ~ P_n(v)} [\log(\sigma(-s(f(u), f(v_n))))] Jpos(u,v)=−log(σ(s(f(u),f(v))))−i=1∑KEvn Pn(v)[log(σ(−s(f(u),f(vn))))]
其中σ\sigmaσ是sigmoid函数,Pn(v)P_n(v)Pn(v)是从图中抽取负例的分布(通常与度数成正比),vnv_nvn是第 iii 个负例。
最终node2vec要优化如下目标函数:
maxfJ=∑(u,v)∈DJpos(u,v)\max_f J = \sum_{(u,v) \in D} J_{pos}(u,v) fmaxJ=(u,v)∈D∑Jpos(u,v)
其中 DDD 是由随机游走产生的所有正例组成的数据集。
那么推导完毕,代码的复现依然还是上节中浅梦大佬的笔记:
【Graph Embedding】node2vec:算法原理,实现和应用
以及他此项目的GitHub:
https://github.com/shenweichen/GraphEmbedding
Node2Vec代码复现
这里采用他的代码复现一下。根据GitHub中的安装方式安装ge包,然后在examples目录下运行node2vec_wiki.py,该文件代码为:
import numpy as npfrom ge.classify import read_node_label, Classifier
from ge import Node2Vec
from sklearn.linear_model import LogisticRegressionimport matplotlib.pyplot as plt
import networkx as nx
from sklearn.manifold import TSNE# 定义一个函数来评估嵌入效果
def evaluate_embeddings(embeddings):# 从文件中读取节点标签X, Y = read_node_label('../data/wiki/wiki_labels.txt')# 设置训练集比例为80%tr_frac = 0.8print("Training classifier using {:.2f}% nodes...".format(tr_frac * 100))# 使用逻辑回归作为分类器,并用嵌入作为特征clf = Classifier(embeddings=embeddings, clf=LogisticRegression())# 划分训练集和测试集,并评估分类效果clf.split_train_evaluate(X, Y, tr_frac)# 定义一个函数来可视化嵌入结果
def plot_embeddings(embeddings):# 从文件中读取节点标签X, Y = read_node_label('../data/wiki/wiki_labels.txt')emb_list = []for k in X:emb_list.append(embeddings[k])emb_list = np.array(emb_list)# 使用TSNE降维到二维空间model = TSNE(n_components=2)node_pos = model.fit_transform(emb_list)color_idx = {}for i in range(len(X)):color_idx.setdefault(Y[i][0], [])color_idx[Y[i][0]].append(i)# 根据不同标签画出不同颜色的点 for c, idx in color_idx.items():plt.scatter(node_pos[idx, 0], node_pos[idx, 1], label=c)plt.legend()plt.show()if __name__ == "__main__":# 从文件中读取图数据,创建有向有权图对象 G=nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using = nx.DiGraph(), nodetype = None, data = [('weight', int)])# 创建node2vec模型对象,设置相关参数 model = Node2Vec(G, walk_length=10, num_walks=80,p=0.25, q=4, workers=1, use_rejection_sampling=0)# 训练模型,设置窗口大小和迭代次数 model.train(window_size = 5, iter = 3)# 获取节点嵌入结果 embeddings=model.get_embeddings()# 调用之前定义的函数,评估和可视化嵌入效果 evaluate_embeddings(embeddings)plot_embeddings(embeddings)
其中wiki_label中是17类,即0到16,我们可以运行该文件,查看输出结果:
R740:/home/program/test/GraphEmbedding/examples# python3 node2vec_wiki.py
Preprocess transition probs...
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 3.7s finished
Learning embedding vectors...
Learning embedding vectors done!
Training classifier using 80.00% nodes...
/home/anaconda3/envs/open-mmlab/lib/python3.7/site-packages/sklearn/metrics/_classification.py:1580: UndefinedMetricWarning: F-score is ill-defined and being set to 0.0 in labels with no true nor predicted samples. Use `zero_division` parameter to control this behavior._warn_prf(average, "true nor predicted", "F-score is", len(true_sum))
/home/anaconda3/envs/open-mmlab/lib/python3.7/site-packages/sklearn/metrics/_classification.py:1580: UndefinedMetricWarning: F-score is ill-defined and being set to 0.0 in labels with no true nor predicted samples. Use `zero_division` parameter to control this behavior._warn_prf(average, "true nor predicted", "F-score is", len(true_sum))
-------------------
{'micro': 0.6756756756756757, 'macro': 0.5947126880104103, 'samples': 0.6756756756756757, 'weighted': 0.6743062291097495, 'acc': 0.6756756756756757}
/home/anaconda3/envs/open-mmlab/lib/python3.7/site-packages/sklearn/manifold/_t_sne.py:783: FutureWarning: The default initialization in TSNE will change from 'random' to 'pca' in 1.2.FutureWarning,
/home/anaconda3/envs/open-mmlab/lib/python3.7/site-packages/sklearn/manifold/_t_sne.py:793: FutureWarning: The default learning rate in TSNE will change from 200.0 to 'auto' in 1.2.FutureWarning,
日志输出中打印了几个评估函数,它们的具体分数为:
{'micro': 0.6756756756756757, 'macro': 0.5947126880104103, 'samples': 0.6756756756756757, 'weighted': 0.6743062291097495, 'acc': 0.6756756756756757}
相关的聚类图如下:
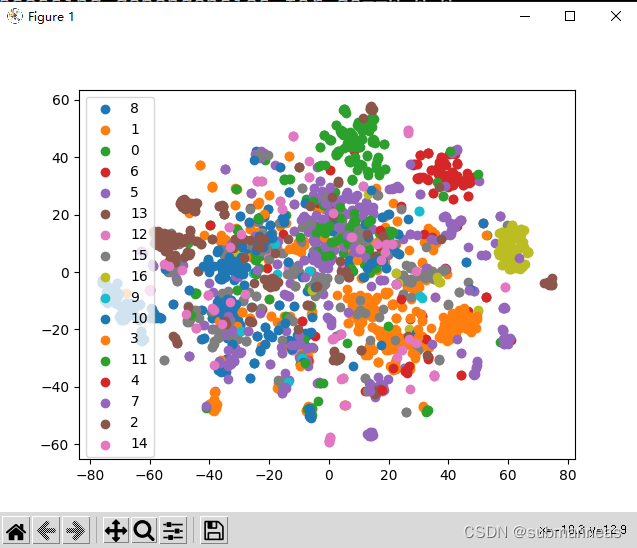
关于node2Vec的底层代码,可以查看上面提到的链接,有解释源码中的preprocess_transition_probs、get_alias_edge和node2vec_walk,第一个函数是构造采样表,第二个函数是概率转换,即开头我所提到的创新,将随机游走变为了概率游走,第三个函数就是加入了alias sample算法的采样器。
当然,node2vec自己也创建了一个包,直接根据pip install node2vec下载,算是官方包,也是视频课程所用到的。
node2Vec包实战
本节根据B站视频同济子豪兄相关说明,代码参考自Task05 Node2Vec论文精读
1. 导入工具包与默认安装的数据集:
import networkx as nx
import numpy as np
import randomimport matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False # 《悲惨世界》人物数据集
G = nx.les_miserables_graph()
2. 构建Node2Vec模型
from node2vec import Node2Vec# 设置node2vec参数
node2vec = Node2Vec(G, dimensions=32, # 嵌入维度p=1, # 回家参数q=3, # 外出参数walk_length=10, # 随机游走最大长度num_walks=600, # 每个节点作为起始节点生成的随机游走个数workers=4 # 并行线程数
)# p=1, q=0.5, n_clusters=6。DFS深度优先搜索,挖掘同质社群
# p=1, q=2, n_clusters=3。BFS宽度优先搜索,挖掘节点的结构功能。# 训练Node2Vec
model = node2vec.fit(window=3, # Skip-Gram窗口大小min_count=1, # 忽略出现次数低于此阈值的节点(词)batch_words=4 # 每个线程处理的数据量
)
X = model.wv.vectors

3. 节点Embedding聚类可视化
# KMeans聚类
from sklearn.cluster import KMeans
import numpy as np
cluster_labels = KMeans(n_clusters=3).fit(X).labels_
print(cluster_labels)# 将networkx中的节点和词向量中的节点对应
colors = []
nodes = list(G.nodes)
# 按 networkx 的顺序遍历每个节点
for node in nodes:# 获取这个节点在 embedding 中的索引号idx = model.wv.key_to_index[str(node)] # 获取这个节点的聚类结果colors.append(cluster_labels[idx])
"""
[0 0 0 0 0 2 2 0 2 1 2 2 0 0 0 0 2 0 0 0 2 2 1 1 1 1 1 1 1 0 0 0 0 0 0 0 02 0 0 0 2 2 0 2 2 2 2 0 0 0 0 0 2 0 0 1 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0]
"""
4. 可视化聚类结果
plt.figure(figsize=(15,14))
pos = nx.spring_layout(G, seed=10)
nx.draw(G, pos, node_color=colors, with_labels=True)
plt.show()

node2vec降维可视化
# 将Embedding用PCA降维到2维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
embed_2d = pca.fit_transform(X)plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.show()

还可以对Edge(连接)做Embedding:
from node2vec.edges import HadamardEmbedder# Hadamard 二元操作符:两个 Embedding 对应元素相乘
edges_embs = HadamardEmbedder(keyed_vectors=model.wv)# 查看 任意两个节点连接 的 Embedding
edges_embs[('Napoleon', 'Champtercier')]"""
array([-1.32887985e-03, 4.66461703e-02, 4.09327209e-01, 9.96602178e-02,6.26228750e-02, 5.16123235e-01, 3.31034124e-01, 8.28218937e-01,7.78538138e-02, 1.39643205e-02, 5.18605635e-02, 7.23598641e-04,3.80857401e-02, 2.59436034e-02, 2.91174115e-03, 2.69687593e-01,3.69817726e-02, 9.54697747e-03, 2.63099521e-01, 1.34550110e-01,8.09033439e-02, 6.05619431e-01, 3.74024451e-01, 8.45154063e-05,1.11978855e-02, -5.34820855e-02, 5.61549842e-01, 8.59113395e-01,1.65469334e-01, 6.88703060e-02, 1.19110994e-01, 6.94330484e-02],dtype=float32)
"""
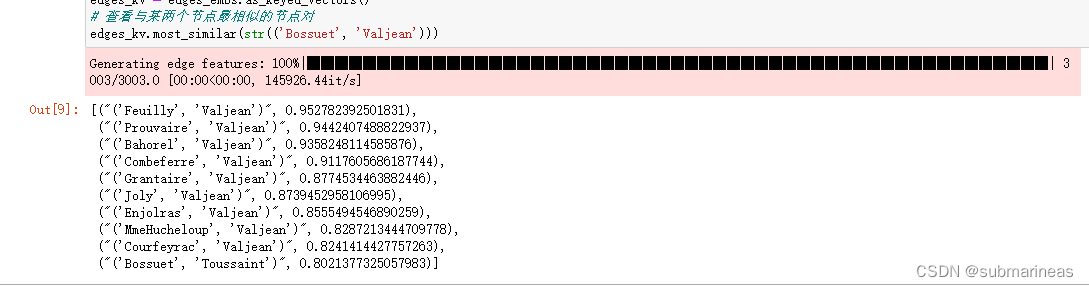
计算# 计算所有 Edge 的 Embedding,查看与某两个节点最相似的节点对:
# 计算所有 Edge 的 Embedding
edges_kv = edges_embs.as_keyed_vectors()
# 查看与某两个节点最相似的节点对
edges_kv.most_similar(str(('Bossuet', 'Valjean')))