名词解释

1、投影模型
一种数学方法，是镜头镜片组的设计的预期目标。

2、镜头投影圆
图像经过镜头后的区域

3、成像面
传感器的成像区域

4、中央和非中央摄像头
经过镜头的光线相交成唯一点为中央镜头，反之，非中央镜头

5、全向相机（Omnidirectional cameras）
可拍摄拍摄全向图像的相机

6、mirror
反射镜

7、lens
透镜

9、折反射全向相机(catadioptric omnidirectional cameras)
使用反射镜与透镜的全向相机

10、折射全向相机(dioptric omnidirectional cameras)
仅仅使用透镜的全向相机

仓库地址

https://github.com/HiYx/study-repository-myself-camera-calibration-easyweave-V1-c-python

1、镜头光路图

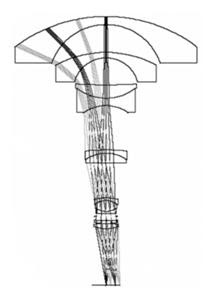
对于鱼眼相机，我们一般将其成像模型用球面，抛物面模型来代替。下面先来看看鱼眼相机的成像光路图：

从图中可以看出，鱼眼相机的成像路径是完全不同于一般的小孔成像的相机。一般的鱼眼相机由以下几个部分组成：

球面投影之后的图像的大小，球面透视投影算法的目标图像是需要扩大的。

同时算法对圆形图像半径的求解依赖很高。不同的半径对校正效果的影响比较大。

2、鱼眼镜头投影模型

鱼眼相机受鱼类眼睛生理结构的启发而产生，鱼眼相机的视场角一般大于 120。
但当视场角大于等于 90。时，基于针孔相机成像模型的线性模型将无法适用于鱼眼相机。

标准鱼眼相机的镜头一般由多层镜片组构建，因此其光学设计结构复杂。光线进入鱼眼相机经过多次折射后，再投影到相机的传感器上成像。

从数学理论分析，若对鱼眼相机的投影曲线进行拟合，便可得到合适的鱼眼相机成像模型的数学公式；从光学原理分析，利用“非相似”成像机制，通过对物理空间挤压，必将引入不可忽视的畸变（多为径向的桶形畸变）来达到对鱼眼相机成像模型的描述；由于光学系统产生畸变的程度由主光线的路径所决定，因此必会导致所成图像有一定程度的形变。

虽然“物”与“像”之间产生了形变，但从 3 维物理空间的“物”到 2 维图像平面的“像”之间仍然是一一对应的映射关系，因此 “非相似”成像机制的可行性得以被保障。

四种模型（指导镜头的设计）

常见的鱼眼相机基本成像模型主要有四种，它们分别是等距投影、等立体角投影、体视投影、正交投影。

镜头的设计基本是按照上述四种投影模型而制作的，可看出鱼眼相机成像模型通用性较差。

为了解决模型通用性较差的问题，可以引入畸变模型，将鱼眼成像模型等价成理想针孔成像模型与畸变模型的叠加作用。（我们后面再写文章来说明这个事情）

1、等距投影（最广泛）

r=f.a
适用于视角大于180°场景，价格亲民

r是在成像平面上，对象到光轴的距离
f是镜头的焦距
a是入射光线与光轴的夹角

等距投影成像模型中径向距离与入射角呈单倍数的正比例关系，故而使用这类鱼眼相机，其成像计算较为方便，算法复杂度较低，可具有实时性，因此等距投影模型是实际应用中最广泛的鱼眼相机成像模型。

等距投影模型，我们可以认为相机的成像模型实际上表征的是成像的像高与入射角之间的关系。

公式中r表示的是传感器上成像的像高。f表示的是相机的焦距。a 表示的是入射角的大小。

成像模型实际上是为了用来描述入射角与成像像高之间的映射关系，等距投影是以线性关系来定义，等立体角投影模型是用正弦函数来定义，立体视觉投影是以正切函数来定义的。那么如何来理解所谓的等距投影呢？先来看看等距投影的示意图：

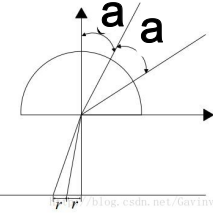
从图中可以看出以相同增量的入射角a来进行投影，等距投影模型将这些相同增量位置的像素投影到成像面上的时候所得到的像高是相等的。

其实这个关系从等距投影的r的表达式上也可以看出来。

首先我们需要明确等距模型只是给出了入射角和相机焦距之间的关系。

这个关系的使用本质上还是需要带入到球面模型或者抛物面模型中取求解坐标映射关系。
但球面投影模型下的图像是有一定扩展的也就是说球面投影时我们的目标图像的大小相对于原图来讲需要在一定程度上进行扩大。扩展的依据就是在一定程度上要符合人眼的视觉效果按宽高比4:5来设置目标图像的大小。

同时，半径的确定是至关重要。如果半径误差大，映射视场范围小于鱼眼图像实际的圆形区域。

2、正交投影模型

光心无限远
r=f.sin a
映射关系简单，图像中心畸变小
边缘图像失真严重，仅适用视角小于180°的场景

r是在成像平面上，对象到光轴的距离
f是镜头的焦距
a是入射光线与光轴的夹角

当a = 90°时，三维场景在相机的镜头边缘所成的像是一条直线，这便损耗相机的成像空间了，这种成像模型被称为正交投影。该模型的畸变程度与其他模型相比都要大一些。

3、等立体角投影

r=2f.sina/2
图像不失真
映射关系较为复杂

比较常用的成像模型也包括等立体角投影方式，其一般应用于一些类似摄影、航天测绘等场景。

4、体视投影模型

r=2f.tana/2
对视角接近180°的图像压缩较小
成像面积小，畸变较大，价格昂贵

该投影模型的入射角不会超过 180°。

2.x 总结

镜头的设计基本是按照上述四种投影模型而制作的，可看出鱼眼相机成像模型通用性较差。为了解决模型通用性较差的问题，J.Kannala[9][10]引入畸变模型，将鱼眼成像模型等价成理想针孔成像模型与畸变模型的叠加作用。Weng[18]提出镜头畸变模型可以被分解成三个部分：切向畸变（偏心畸变）、薄棱镜畸变和径向畸变。

但这个观点仅被一些物理背景知识所支撑，缺乏畸变的实际数据作依据。实际上，畸变是由复杂的棱镜系统、相机几何和图像传感器表面（通常都不是很平）的累计作用。因此为了解决鱼眼相机标定方法不统一的问题，需要建立一种合适的鱼眼畸变模型来给定鱼眼相机的标定框架。

目前，常用的鱼眼相机畸变模型有：径向模型、除法模型、FOV 模型、多项式模型和有理式模型等。

3、投影圆和成像面

圆形鱼眼图

鼓型鱼眼图

全帧鱼眼图

4、中央和非中央摄像头

非中央相机Non Central Cameras

全向相机Omnidirectional cameras通常通过最佳组合镜子mirrors 和透视相机cameras来布置。当来自相机并被镜面反射的光线不相交成唯一点时，相机-反光镜组件称为非中心（即非单一有效视点）系统。检查下面的图像以获得更好的理解。

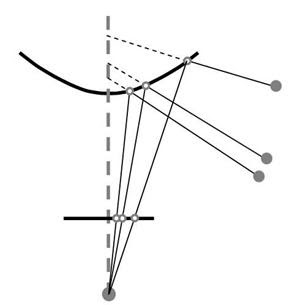
中央摄像头 Central Cameras

相反，中央摄像机是可以完美验证单一有效视点属性的系统。也就是说，每条被镜面反射的光线都会相交成一个唯一的点，称为单一有效视点（请参见下图以更好地理解）。 [3] 中给出了这种成像系统的完整定义和分析。

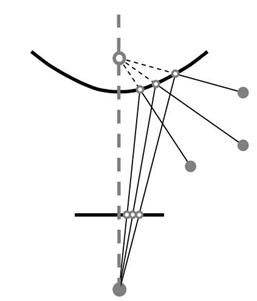
如 [3] 中所述，可以通过将针孔相机（透视相机a pinhole camera (perspective camera)）与双曲面（hyperbolic mirror）、抛物面（parabolic mirror）和椭圆镜（ elliptical mirrors）最佳组合来构建中央全向相机。

[3]  Scaramuzza, D. (2008). Omnidirectional Vision: from Calibration to Robot Motion Estimation, ETH Zurich, PhD Thesis no. 17635. PhD Thesis advisor: Prof. Roland Siegwart. Committee members: Prof. Patrick Rives (INRIA Sophia Antipolis), Prof. Luc Van Gool (ETH Zurich). Chair: Prof. Lino Guzzella (ETH Zurich), Zurich, February 22, 2008.

最近，镜头制造还提供鱼眼镜头，它很好地近似于单一有效视点属性。这些成像系统只需要一个鱼眼镜头来扩大相机的视野，而不需要镜子。前者的相机（同时使用相机和镜子）称为折反射全向相机(catadioptric omnidirectional cameras)，而后者的相机（仅使用鱼眼相机）称为折射全向相机(dioptric omnidirectional cameras)。

对于 catadioptric omnidirectional cameras 折反射全向相机作为中央系统，必须满足以下安排：

• 相机+双曲面镜mirror

相机光学中心（即镜头的中心）必须与双曲线的焦点重合。这确保了镜子反射的光线相交到一个唯一的点（即双曲线的内部焦点）。有关相机 + 双曲面镜的示例，请参见上图。

• 相机+抛物面镜parabolic mirror +正射镜头 orthographic lens

当使用抛物面镜时，所有从世界进入相机的反射光线都平行于镜轴。这意味着针孔相机通常不能按原样使用，因为平行光线不会向相机光学中心会聚。为了在 CCD 平面上提供聚焦图像，必须在相机和抛物面镜之间放置一个正交透镜。检查下面的图像以获得更好的理解。

• 相机+鱼眼镜头 fisheye lens

另一种不使用镜子来扩大相机视野的方法是在相机 CCD 上方添加一个鱼眼镜头。

鱼眼镜头是一种镜头系统，能够将相机的视野扩大到 190°（见下图）。

使用鱼眼镜头的相机不是一般的中央系统，但它们非常接近单视点属性。

镜像(content: mirror) vs. 透镜(lens)

https://www.tl80.cn/article/207090

透镜和反射镜是两种不同的光学器件。镜子是基于反射原理的装置，而透镜是基于折射原理的装置。这两种器件在光学、天文学、摄影等各个领域都非常重要。

镜子的定义

镜子是反射落在镜子上的光的物体。
镜子被定义为一个有光泽的玻璃物体，在它的背面有一层银色的涂层，它反射光线并形成物体的图像，物体就在它的前面。

镜子通常是由涂上一层反光膜制成的。反光涂层由几层不同的材料组成。镜子主要有两种类型。这些是平面镜和曲面镜。曲面镜分为凹镜和凸镜两类。镜子是根据反射原理工作的。任何表面的反射原理是入射角和反射角相等。这些角度是从入射点的反射面上画的法线测量的。这条线也在包含入射光和反射光的平面上。

它有两种类型：

• 平面镜：平面镜称为平面镜。它产生虚拟和直立的图像。
  Spherical mirror: A mirror that has a curved surface, which is used to form a diminished or magnified image, is called a spherical mirror. It is of two types convex and concave mirror, as described below:
• 凸面镜：从曲面反射的镜子是凸面镜。在这样的镜子里，里面是上漆的，外面是抛光的，这反映了图像。它是一个发散的镜子，形成了摆在前面的物体的虚拟和直立的图像。
• 凹面镜：凹面镜是反射面向内弯曲，其表面朝向球体的中心。它是一面会聚的镜子。

透镜

透镜是用于光学和其他相关领域的器件。透镜通过折射来操纵光线。镜子有几种类型。它们是双凸、平凸、正弯月面、负弯月面、平凹和双凹。镜片也可分为简单镜片和复合镜片。透镜用于望远镜、眼镜、隐形眼镜、照相机和其他各种用途。一个完美的透镜能折射出所有入射到它身上的光。镜片是通过将玻璃或透明塑料磨成所需形状来**的。镜子的折射服从斯内尔定律。

透镜意味着一块透明材料，即玻璃或塑料，有两个相对的表面，其中一个或两个是弯曲的。 透镜可以单独使用，也可以是光学装置中两个或两个以上简单透镜的组合，以便通过会聚光束产生图像。

透镜的工作原理是基于折射原理的，即光线通过透镜后发生弯曲，因此其方向发生变化，这就是为什么从透镜可见的物体看起来比实际物体大或小的原因。有两种类型的凸透镜和凹透镜，如下所述：

• 凸透镜：凸透镜的表面从中心向外弯曲，使光线会聚。**望远镜、望远镜、放大镜等都使用这种透镜。
• 凹透镜：凹透镜有一个向中心向内凸出的表面，因此它使光束发散。它主要用于电视放映机。