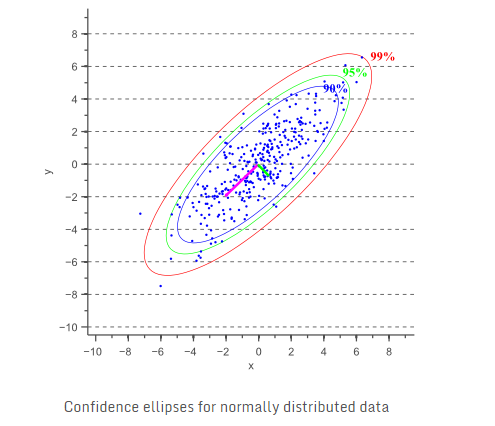
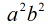直接上图

 

下面附上部分变化的代码：

clear,clc
syms x y a b u v theta
%标准椭圆
f1= x^2/a^2 + y^2/b^2  - 1
%按向量(u,v)平移
f2= (x+u)^2/a^2 + (y+v)^2/b^2  - 1
%主轴相对于x轴旋转theta角度
%旋转前(x',y'),旋转后x = x'cos(theta) - y'sin(theta); y=y'cos(theta)+x'sin(theta)
%所以：x'=ysin(theta)+xcos(theta); y'=ycos(theta)-xsin(theta)
%旋转后
f3= (x*cos(theta)+y*sin(theta)+u)^2/a^2 + (y*cos(theta)-x*sin(theta)+v)^2/b^2  - 1
%将f3展开ps1=expand(f3)

下面是一个变换实例

clear,clc,close all
%绘制标准椭圆
t=0:pi/360:2*pi;
a=4;b=3;
x = a*cos(t);
y = b*sin(t);
plot(x,y,'LineWidth',2),hold on
plot(0,0,'p','MarkerFaceColor','g','MarkerSize',10)
axis on
%对标准椭圆进行旋转和平移
u = 5;v=6;theta =50;
X = (x*cosd(theta) - y*sind(theta) + u);
Y = (x*sind(theta) + y*cosd(theta) + v);hold on,grid on
plot(X,Y,'r','LineWidth',2)
hold on
plot(u,v,'s','MarkerFaceColor','b','MarkerSize',10)
title('椭圆的变换')
xlabel('x轴');
ylabel('y轴');

结果如

参考：

[1]椭圆维基百科