1.凸函数的定义

        凸函数直观上来说，就是两点之间的函数值小于两点连线的函数值

        常见凸函数

线性函数既是凸函数，也是凹函数

对于二次函数，如果Q矩阵是半正定矩阵，那么它的二阶导为Q为半正定矩阵，根据凸性判定的二阶条件，它也是凸的。

最小二乘函数总能够写成AA^T，因此也是凸的 

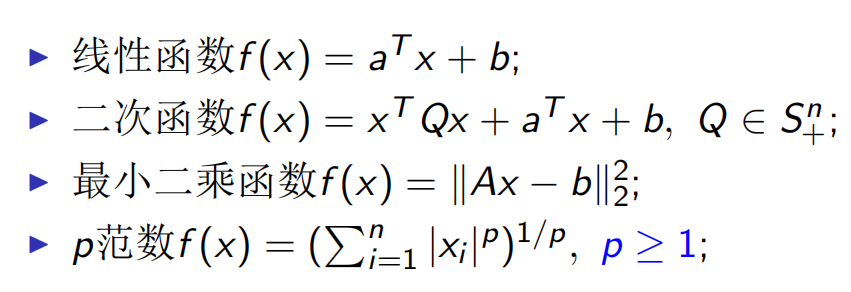
 2.凸函数的性质

       

这条性质讲的是，凸函数的函数值大于等于凸函数在任意一点的切线

 

 

 

这个性质我们可以类比高等数学中函数的凹凸性来理解，当然，同济版高等数学和这里是反的，当二阶导大于0时，f(x)为凸函数。 

充分性 

 必要性

 3.保凸运算

凸函数的非负组合的二阶hesse矩阵肯定半正定，故非负组合是凸的

凸函数求最大也还是凸的 

 

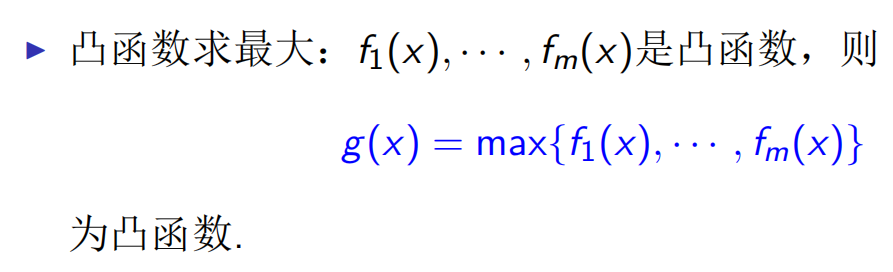
 4.凸集与凸函数之间的关系

        这个含义是说，以一元函数为例，凸函数的下水平集为连通的线段，根据凸集的定义，肯定是凸集，而非凸函数的下水平集不是连通的，肯定不是凸集