电子罗盘原理

1、电子罗盘简介

电子罗盘是一种重要的导航工具，能实时提供移动物体的航向和姿态要实现电子罗盘功能，需要一个检测磁场的三轴磁力传感器和一个三轴加速度传感器。

地球是存在磁场的，地球的磁场象一个条形磁体一样由磁南极指向磁北极。在磁极点处磁场和当地的水平面垂直，在赤道磁场和当地的水平面平行，所以在北半球磁场方向倾斜指向地面。用来衡量磁感应强度大小的单位是Tesla或者Gauss（1Tesla=10000Gauss）。随着地理位置的不同，通常地磁场的强度是0.4-0.6 Gauss。需要注意的是，磁北极和地理上的北极并不重合，通常他们之间有11度左右的夹角。

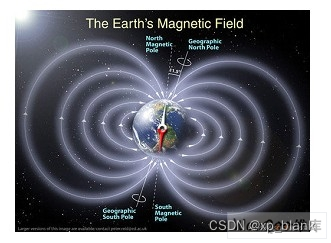
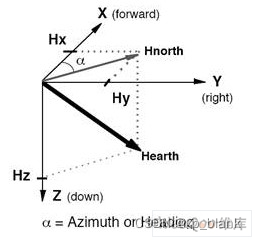
地磁场是一个矢量，对于一个固定的地点来说，这个矢量可以被分解为两个与当地水平面平行的分量和一个与当地水平面垂直的分量。如果保持电子罗盘和当地的水平面平行，那么罗盘中磁力计的三个轴就和这三个分量对应起来。通过计算就可以计算航向角了。但是在实际应用中，但是更多的时候设备并不是保持水平的，通常它和水平面都有一个夹角。这个夹角会影响航向角的精度，所以需要通过加速度传感器进行倾斜补偿

2、姿态简介

2.1 姿态是什么

在了解如何进行倾角补偿前，需要先了解什么是姿态。想象一架飞机准备起飞，于是它在机场跑道上进行一段加速助跑，达到一定速度后，机头抬升15度，腾空而起，离开了地面。然而由于起飞时的方向和目标方向相差甚大，于是飞机调转机头，最终往北偏东30度的方向飞去。

这个过程中，根据日常生活经验，我们如此说明飞机在起飞过程中的发生的变化：“抬升15度”，“北偏东30度”。也就是说，通常我们会使用 “角度”，来表示一个物体的姿态。那这个角度大小是如何得来的？其中，“15度”指飞机机身与水平地面的夹角，“北偏东30度”则指飞行方向与正北方向的夹角。也就是说，日常生活中我们描述物体的姿态，是以脚下的大地作为参考的。通常人类在太空中会失去方向感，是因为地球上的重力加速度的存在让我们始终能够以大地作为参考物，而失重环境下失去了参考物，我们便无法感知自身以及周围物体的姿态了。

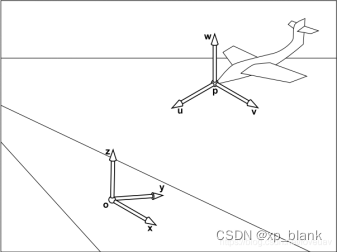
为了方便描述物体之间的方位关系，定义了两个坐标系：大地坐标系0-xyz和机体坐标系P-uvw，坐标系可以自己定义，但必须选择一个坐标系作为参考坐标系，通常选择大地坐标系作为参考坐标系。姿态就是表示这两个坐标系之间的关系。

2.2姿态表示方法

了解了姿态的定义后，我们又面临着一个问题，如何使用数学方式来描述姿态，以便下一步的计算？

欧拉角是最直观的一种姿态描述方式，其定义为：一个坐标系到另一个坐标系的变换，可以通过绕不同坐标轴的3次连续转动来实现。这三次的转动角度统一称之为欧拉角。但有一点值得注意的是，欧拉角并不直接等同于我们常说的姿态角。欧拉角由三次绕轴旋转组成，而这三次转动顺序任意，且转动轴可以是参考系的，也可以是机体系的，因此共有24种转动方式。而通常飞控上所使用的姿态角，指的是航空领域主要应用的航空次序欧拉角，也叫卡尔丹角（Tait-Bryan angles），定义欧拉角的转动顺序为Z-Y-X。其中绕Z轴转动为偏航角（Yaw），绕Y轴转动为俯仰角（Pitch），绕X轴转动为横滚角（Roll），其具体意义如下：

偏航角（Yaw）：机体系x轴投影到水平面与参考系x轴的夹角，顺时针旋转为正。

俯仰角（Pitch）：机体系x轴与水平面的夹角，抬头为正。

横滚角（Roll）：机体坐标系z轴与通过机体系x轴的铅垂面间的夹角，机体右旋为正。

实际要解决的问题就是计算这三个量，就需要了解一下旋转的数学规律。下图是绕Z轴旋转后，世界坐标系和机体坐标系之间的关系。

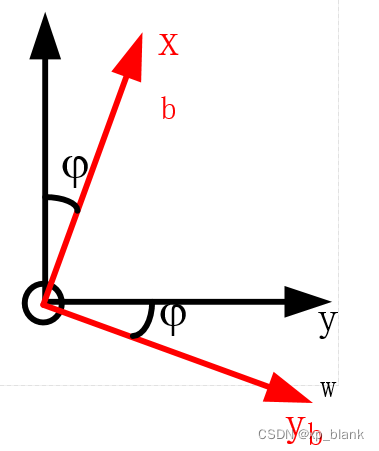
在b系中的下x，y，z在w系中则分别为

因此绕z轴旋后，b系到w系的旋转矩阵为：

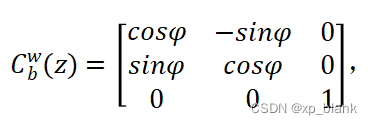
同理可得，绕y轴的旋转矩阵为：

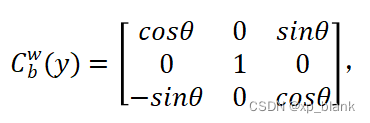
同理可得，绕x轴的旋转矩阵为：

一次欧拉角转动的旋转矩阵为：

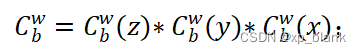
展开得到b系到w系的旋转矩阵为：

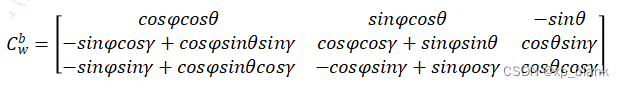
这个矩阵是一个正交矩阵。所以w系到b系的旋转矩阵为：

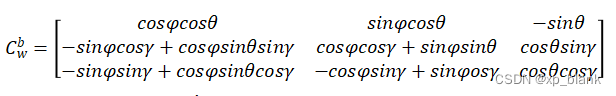
从w系到b系的转换为：，在匀速或者静止状态下，在b系测得的加速度值为加速度计读到的值，在w系，绕Z轴的旋转对求解和无影响，故可以令；然后就可以得到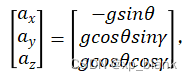：，可以求得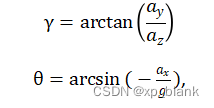

由于地磁始终指向正北，所以，在w系中，正东方向的磁分量为0，设此时的值为,经过一定角度的旋转后，在b系中的值为磁力计读取的值，它们之间满足：

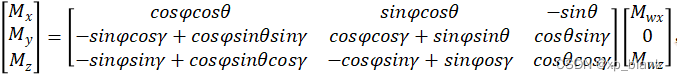
由上式消元可得：

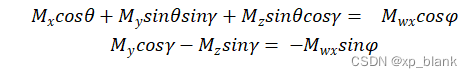
由此可得：

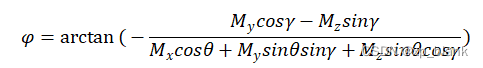
至此：三个欧拉角就可以解出来了。

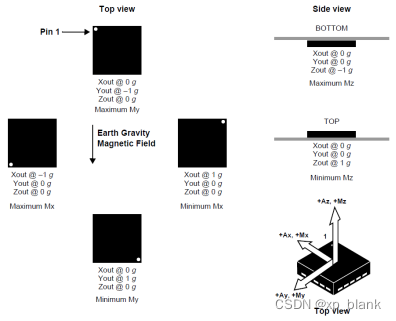
在实际应用中，芯片会有一个坐标轴，安装在机体上，不一定与机体坐标轴重合，因此需要将芯片坐标轴转换到机体坐标系中。

3.传感器校准

3.1传感器为什么需要校准

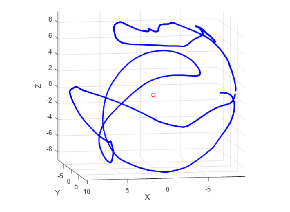
工厂按照特定的技术及工艺标准制造生产出一批传感器，这些传感器中所有个体的实际状态处于一个随机分布且均值为期望误差的序列上，简单来说，就是同一批次的传感器，误差各不相同，但是在一定范围之内的。对于磁力计，地球磁场在一般情况下只有微弱的0.5高斯，而一个普通的手机喇叭当相距2厘米时仍会有大约4高斯的磁场，一个手机马达在相距2厘米时会有大约6高斯的磁场及其容易受到干扰，因此需要校准。对于加速度计，只需要出厂校准一次就够了，而对于磁力计，则需要检测到周围磁场强度发生较大变化时候，需要再次校准。

3.2误差数学模型

根据实际情况，误差类型可总结为两类误差：刻度误差和零偏误差。

设x，y，z三个轴的零偏误差和刻度误差分别为，当前时刻的真实值为测量值为x、y、z。则有下列方程：

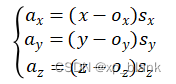
在静止状态下，不管设备处于何种状态，器加速度的模值必然为重力加速度g。则有：

即：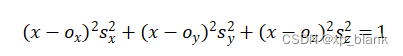

即为我们要求解的量，x、y、z为传感器读取的值，为已知量。

对于上述误差方程的求解，理论上，6个未知量，采集6组值，得到6个方程就可以求解。但是实际上，从传感器中获取到的值是有随机噪声的，导致求解未必精确。对于线程方程通过高斯消元很容易求得精确解，但是对于非线性方程，大部分时候，是没有办法直接求得精确解的，为了解决这个问题，可以通过最小二乘法求得其近似解。首先构建误差方程

对于方程组而言，其误差的平方和函数为：

，

于是目标方程就变成了S取极小值时的。在极值处有。在初始解处，对进行泰勒展开式可以得到下式：

对于我们要求解的误差方程，是一个6元函数，假设其自变量矩阵为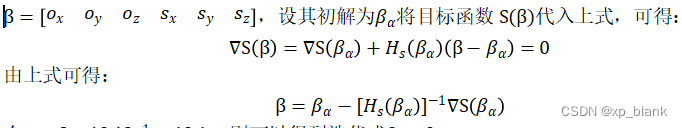

这样就可以得到一个线性方程组，解出，然后更新，从而迭代，不断逼近最优解。实际应用中，高斯牛顿法有着如下缺点：

（1）初始点选取较为严苛，若初始点距离极小值点过远，迭代步长过大会导致迭代下一代的函数值不一定小于上一代的函数值。

（2）高斯牛顿法中的Hessian矩阵在某些情况下可能是非正定的（不可逆），残差r 过大时可能导致高斯牛顿法无法收敛。

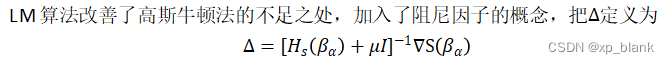
当 $\mu$ 很大时，其效果越接近梯度下降算法，当 $\mu$ 趋近于0时，越接近高斯牛顿法。使用LM法时，需要加入一些 $\mu$ 的调整策略，使得距离解较远的时候，使用梯度下降法，距离极小值较近的时候，使 $\mu$ 减小，这样就近似高斯牛顿法，能得到比梯度下降法更快的收敛速度。对于加速度计的校准，就是六个面静止状态下，采集6个值带入r计算残差，作为初始解开始迭代。