之前写的一个关于FAST-LIO论文阅读的总结，可以参考FAST-LIO论文阅读参考链接

FAST-LIO2是港大MaRS实验室在FAST-LIO框架的基础上进行了修改而成，集成了他们课题组的几个工作，形成了一个非常优秀且极具代表性的框架。

论文：FAST-LIO2: Fast Direct LiDAR-Inertial Odometry
源码链接
FAST-LIO2简明公式推导
ikd-tree解析

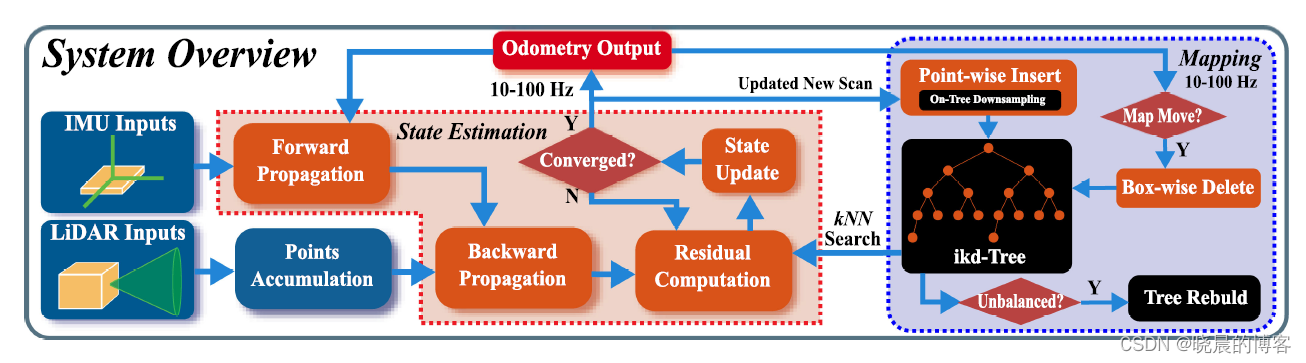
系统的整体框架如下，与FAST-LIO相同仍然使用了一个紧耦合迭代扩展卡尔曼滤波（红色框内）。不同的地方主要在于1）直接使用输入的激光雷达原始点进行配准，去除了特征提取模块；2）增加一个ikd-tree的数据结构，能够快速的查询、增删，提高效率。

整体的突出贡献有以下三个部分：

1. 提出一个iKd-tree的数据结构，能够高效查询，增量式建图。除了高效的近邻点搜索，新的数据结构还支持增量式地图更新（即点插入，在树上进行下采样，以及点删除）还能在最小化计算代价的前提下进行动态重平衡。
2. 基于ikd-tree计算效率的提高，去除了特征提取模块，能够直接配准原始点。在剧烈运动以及杂乱的环境中更加准确、可靠。
3. 把上述两项技术（ikd-tree与直接配准），结合到FAST-LIO（紧耦合的雷达惯性里程计，流形上的迭代卡尔曼滤波）中。

下面对系统的各模块分别进行介绍：

迭代扩展卡尔曼滤波

FAST-LIO论文阅读参考链接
算法的整体流程如下：

增量式kd-tree（ikd-tree）

增量式维护示意图

下图为Fast-LIO2框架中对地图进行区域管理和维护的二维演示：

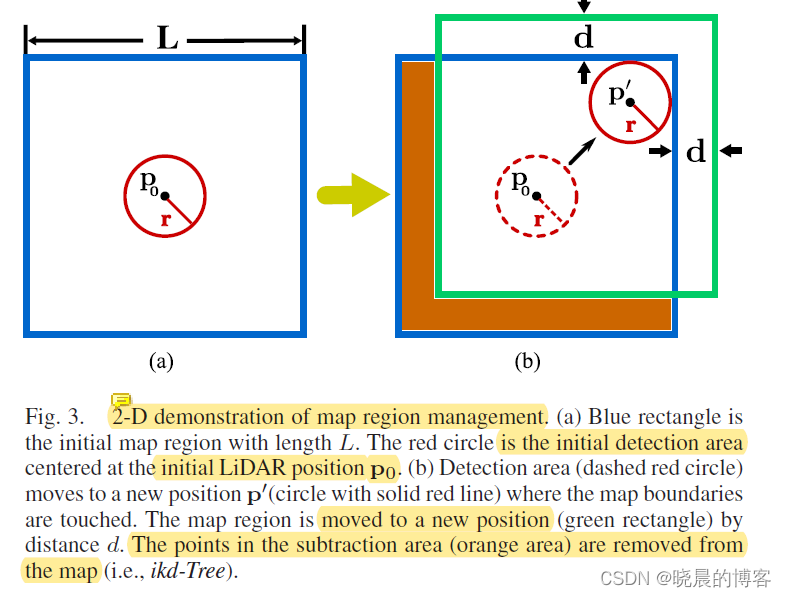
地图点通过一个ikd-tree进行维护，通过不断融合新的扫描点，地图的区域也不断增大，但是地图不能无限制的增大，所以在当前的位置设置了一个长度为$L$的局部区域，如上图（a）中所示。检测区域为计算的激光雷达位姿（位置）为中心，$r$为半径的球（$r=\gamma R$，其中$R$为激光雷达的测距范围，$\gamma$为一个大于1的松弛参数）。当新位置$p^{{}^{\prime }}$处的检测球与地图边缘相交时，地图将会移动距离$d=(\gamma -1)R$，如上图（b）中所示，橙色区域将会被通过盒式操作删除。

ikd-tree基本结构与构建

已有的K-D tree只在叶子节点 存储一系列的点，而ikd-tree在叶子节点与内部节点均存储点（一个节点对应一个点，后续将不加区分的使用二者），以更好的支持动态点插入与重新平衡。下表中为一个节点的数据结构。

point：其中存储了点信息，如坐标，强度之类的。
leftchild/rightchild：指向左、右孩子节点的指针。
axis：划分空间的分割轴。
treesize：以当前点为根的子节点数量。
range：外接的轴对齐立方体。由两个对角点组成，每个维度的最大最小坐标。

ikd-tree的构建过程：与静态kd-tree的构建过程类似，ike-tree不断根据最长维度的终点进行划分空间，直到子空间中只有一个点。kd-tree数据结构的属性在构建过程中被初始化，包括（子）树的大小与距离信息，初始值如下表中所示。

ikd-tree的增量更新（Incremental Updates）

增量式更新在ikd-tree中被称为增量式操作，接着是动态重平衡。增量式操作包含两种类型：点式操作、盒式操作。点操作是在kd tree中插入、删除或重新插入一个单独的点。而盒式操作是对一个轴对齐立方体中的所有点进行插入、删除或重新插入操作。两种操作均集成了一个在树上下采样操作，保持地图在一个预定的分辨率。由于FAST-LIO2地图管理的需要，本文只解释了逐点插入和盒式删除操作。

逐点插入与地图下采样

考虑到机器人的应用，ikd-tree支持同时进行点插入和地图下采样操作。如Algorithm2中所示：

对Algorithm2进行描述如下：
给定一个转换到全局坐标系下的点$p$，下采样分辨率$l$。

1. 下采样操作：是算法将空间分割成长度为$l$的小立方体，找到包含点$p$的小立方体$C_D$，仅保存$C_D$中最靠近中心的点。实现流程为：首先在kd tree上搜索所有包含在立方体$C_D$的点，与新插入点一起存储在一个数组$V$中。之后，比较数组$V$中的所有点与小立方体$C_D$中心点$p_{center}$之间的距离，仅保留$V$中的最近点$p_{nearest}$。把保留的点$p_{nearest}$插入到kd tree中。

2. 逐点插入：11-24行中的逐点插入是递归执行的，算法从根节点进行递归搜索，直到找到一个空的节点，并添加新的节点。在每一个非空节点，新的点与存储在树节点上的点在分割维度上进行比较，以进一步递归。插入过程中访问过节点的treesize, range属性会更新为最新的信息（line 21）。（line 22）中检查了插入新点后子树的平衡性，以保持ikd-tree的平衡性质。

使用lazy labels的盒式删除

在删除过程中使用lazy labels的策略，即点不会立即被从树上移除，而仅被标记为“deleted”(TABLE 1中的deleted值被标记为true)，如果节点$T$处的子树中的所有节点均被标记为“deleted”，则节点$T$的$treedeleted$属性被标记为$true$。在重新构建过程中，被标记为“deleted”的点将会被从树中移除。

盒式删除操作依靠$range$属性中的范围信息以及树节点中的lazy labels策略进行实现。假设，针对一个节点$T$，其对应的空间范围为立方体$C_T$，需要从以节点$T$的（子）树中删除立方体$C_O$中的点。操作步骤如下：

1. 如果立方体$C_O$与立方体$C_T$之间没有交集，则直接返回，不需要更新ikd-tree。(line 3)
2. 如果立方体$C_O$完全包含立方体$C_T$，则删除节点$T$，设置$deleted$属性与$treedeleted$属性均为$true$，$invalidnum$属性设置为树的尺寸。(line 4~6)
3. 如果立方体$C_O$与立方体$C_T$部分相交，但不完全重叠，则对当前点及左右子节点进行递归操作(line 7~11)。当盒式删除递归操作完成后，同样做了属性更新与重平衡(line 12-13)。

属性更新

在每一个增量式操作之后都使用$AttributeUpdate$函数对遍历过的节点属性更新为最新的信息。
$treesize$ 与 $invalidnum$属性：通过求和两个子树节点的对应属性信息以及自身的点信息进行计算。
$range$属性：通过融合两个子节点的范围信息进行确定。
$treedeleted$：如果两个子节点属性为$true$且自身也被删除了，则设置为$true$。

ikd-tree重平衡

ikd-Tree在每次增量式操作之后自动检测平衡性，并通过重建相关的子树进行动态重平衡其自身。

平衡准则

平衡准则由两部分组成，$\alpha -balanced$与$\alpha -deleted$

$\alpha -balanced$：针对一个节点$T$，当其左右子树满足下述条件时，则认为是$\alpha -balanced$的。该条件中$S$为(子)树的尺寸，${\alpha }_{bal}\in （0.5,1）$。由上可知，当${\alpha }_{bal}$接近0.5时则对平衡性的要求也越高。

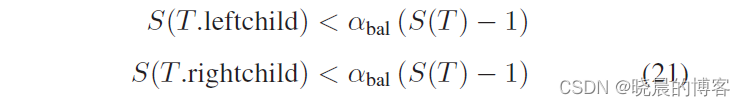
$\alpha -deleted$：针对一个节点$T$，当其无效点（被删除点）数量满足下述条件时，则认为平衡。该条件中$S$为(子)树的尺寸，$I(T)$为（子）树中无效点的数量（节点$T$中的$invalidnum$属性），${\alpha }_{del}\in （0,1）$，当${\alpha }_{del}$接近0，则要求越严格。

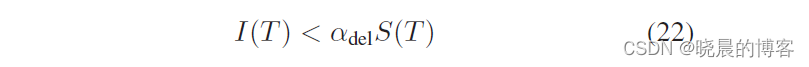
违反上述的任何一个准则将触发一个重建过程，以重新平衡子树。降低树的高度与大小，能够更高效的增量式操作与查询。

重建及并行重建子树

假设对于一个子树$\tau$触发了重建准则（如下图所示），首先把子树展开为一个向量V，并去除其中的无效点(被lazy label标记删除的点)。然后，对向量V中的点进行重建一个更加完美的子树${\tau }^{{}^{\prime }}$。

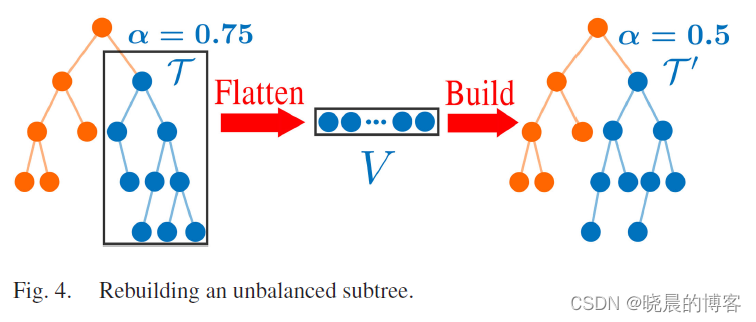
为了避免子树$\tau$过大，重建影响实时性能。使用双线程重建方法来保证高实时性。作者通过一个操作记录器来避免了两个线程间的信息丢失和内存冲突，而不是直接在第二个线程中进行重建，因此在任何时间均保持了k近邻搜索的全部性能。

重建方法流程如Algorithm 4中所示：

当检测到$\alpha -balanced$与$\alpha -deleted$两个平衡准则被违反了之后，需要对子树进行重建。若子树的尺寸小于阈值$N_{max}$则直接在主线程进行重建，反之，则在第二线程进行重建。第二线程的重建算法见$ParRebuild$(line 11-24)。
表示要在第二线程重建的子树为$\tau$，其根节点为$T$
首先，第二线程会锁住所有的增量式更新但不会影响查询（如增删操作，line 12）。随后，第二线程复制子树$\tau$中的所有有效点到向量$V$中，但保留原始的子树不发生变化以防在重建过程中有可能的查询（line 13）。展开之后，原始的子树对主线程打开，可以进行相关的增删操作，但是这些操作同时被记录在了一个$operation$ $logger$的队列中。一旦第二线程中完成了子树的重建操作（line 15）则对重建后的子树${\tau }_{{}^{\prime }}$执行$operation$ $logger$队列的增量式操作（lines 16-18）。当所有的操作都被完成之后，使用新的子树${\tau }_{{}^{\prime }}$来代替原始的子树$\tau$。算法锁住节点$T$以防进行更新，然后查询并替代为$T^{{}^{\prime }}$（line 19-22），最后释放原始子树的内存（line 23）。（注意，这一过程中虽然$LockAll$禁止了所有的操作，但是替换过程是非常快的，所以允许在主线程中及时操作。）$LockUpdates$与$LockAll$这两个操作均通过互斥操作实现。

上述的并行重建设计能够保证在第二个线程中重建过程中，主线程中的建图过程仍然能够在里程计的频率进行而不被任何中断。

KNN搜索

尽管与现有的kd树第三方库的实现类似，ikd-tree中的近邻搜索也做了深入的优化。节点中的$range$属性信息通过 “bounds-overlap-ball”方法用于加速近邻点搜索（详细可参考链接）。以及下图中的说明：

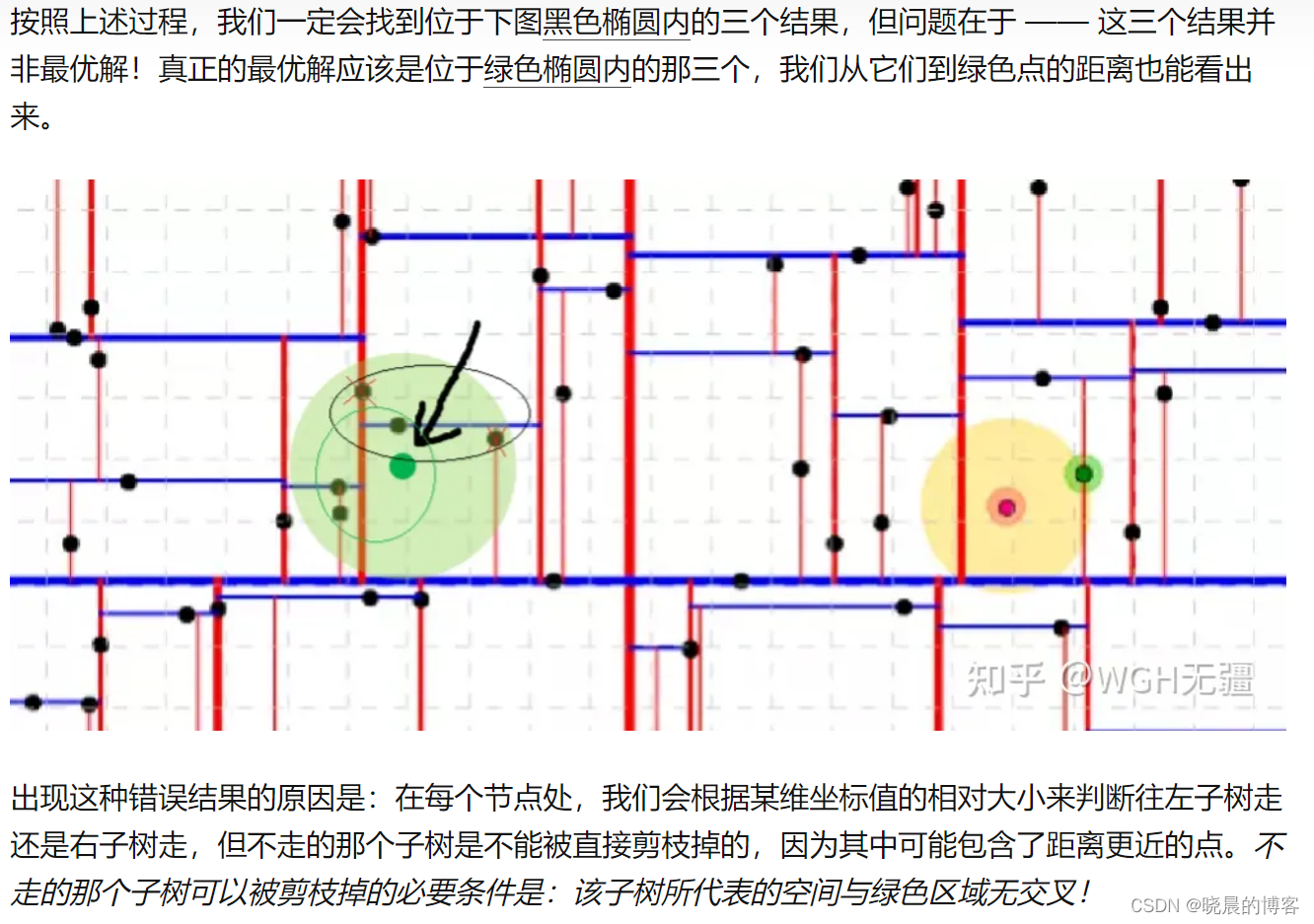
图片来源于知乎大佬无疆的文章

在搜索过程中会根据所遇到的点与目标点之间的最近的k个距离存储在一个队列$q$中。当递归搜索到一个树节点$T$，计算目标点到立方体$C_T$之间的最小距离$d_{min}$，若$d_{min}$大于队列$q$中的最大距离，则此节点及子节点都不用进行搜索处理了，这样就降低了回溯的量，提高时间性能。此外，在FAST-LIO2以及其他的很多LIO算法中都仅使用到达目标点一定距离范围内的点作为内点，参与状态估计。这自然的为KNN搜索提供了最大的搜索距离。还有，ikd-tree支持并行计算结构的多线程KNN搜索。