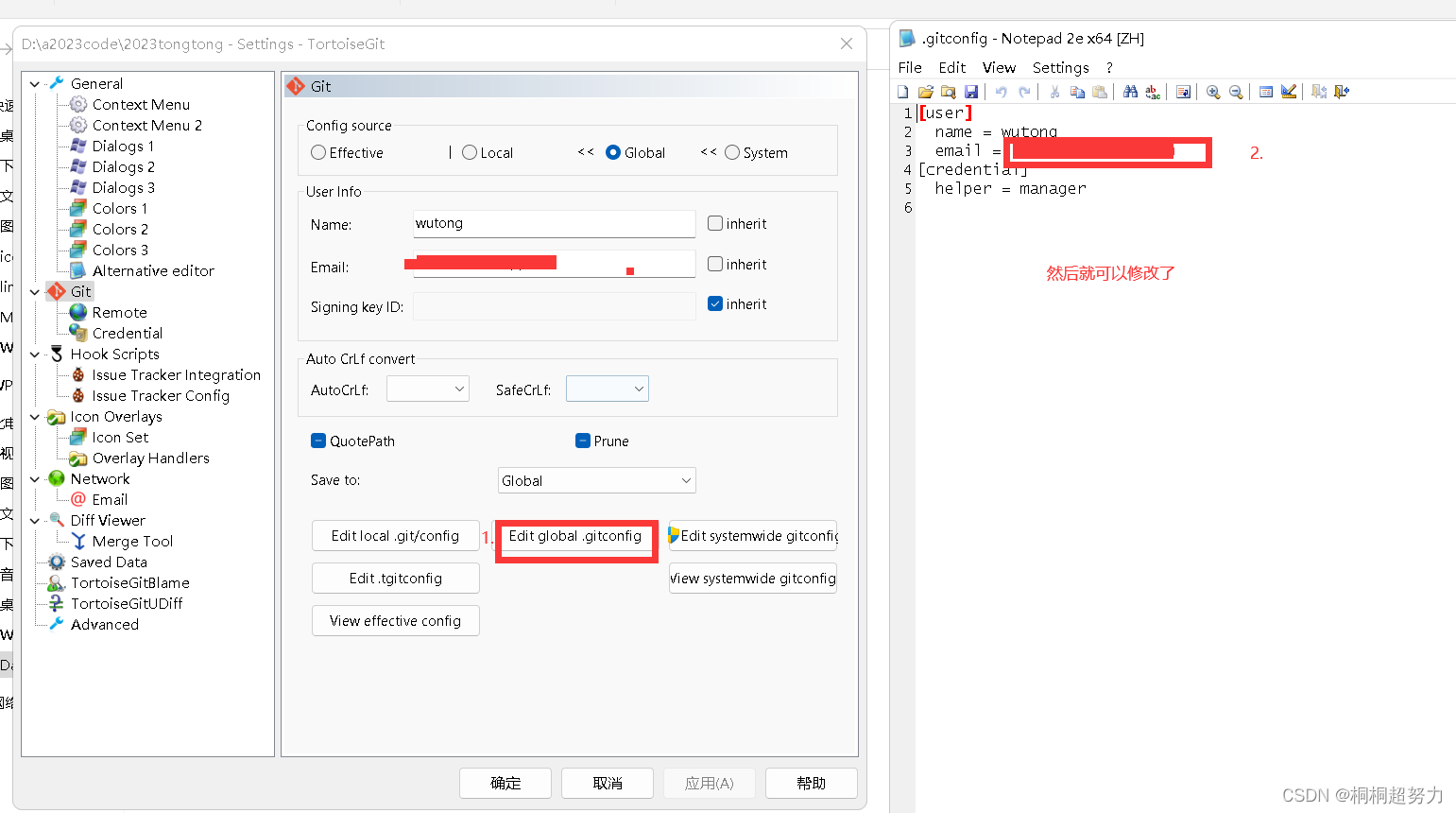
一阶线性微分方程的形式如下：

$$y^{\prime }+p(x)y=q(x)$$

---

对于式子左侧，长得像下式，但不太一样

$$(uv{)}^{\prime }=u^{\prime }v+u{v}^{\prime }$$

$$y^{\prime }\cdot 1+y\cdot p(x)$$

---

这里对应$v$看似得不到一个合适的，但是借助$[e^{f(x)}{]}^{\prime }=e^{f(x)}\cdot f^{\prime }(x)$可以发现能构造出类似的，即下式

$$y^{\prime }\cdot e^{\int p(x)dx}+y\cdot e^{\int p(x)dx}\cdot p(x)$$

提出相同系数：

$$e^{\int p(x)dx}\cdot [y^{\prime }\cdot 1+y\cdot p(x)]$$

原式等号右侧增补相同系数可得到式子整体（待化简）

$$e^{\int p(x)dx}\cdot [y^{\prime }\cdot 1+y\cdot p(x)]=e^{\int p(x)dx}\cdot q(x)$$

---

于是化简得到：

$$[y\cdot e^{\int p(x)dx}{]}^{\prime }=e^{\int p(x)dx}\cdot q(x)$$

左侧是求导，给积回去，右侧得添积分号：

$$y\cdot e^{\int p(x)dx}=\int e^{\int p(x)dx}\cdot q(x)dx+C$$

---

将y系数化为1得最终结论通解公式：

$$y=e^{-\int p(x)dx}\cdot \int e^{\int p(x)dx}\cdot q(x)dx+C$$

且通解就是全部解