一般摄像机简化为小孔成像的理想模型（线性模型），因为摄像机镜头（视场角）很小，相当于被拍摄物体通过小孔投影到感光元件CCD/CMOS上。

对于加了各种镜头的摄像机，镜头不是平面（凸镜凹镜），小孔成像的像发生畸变，属于非线性模型，需要额外矫正。

通过标定可求出摄像机各种内外参数，也包括镜头畸变。

​​​​​​​小孔成像和相机成像略有不同。

​​​​​​​

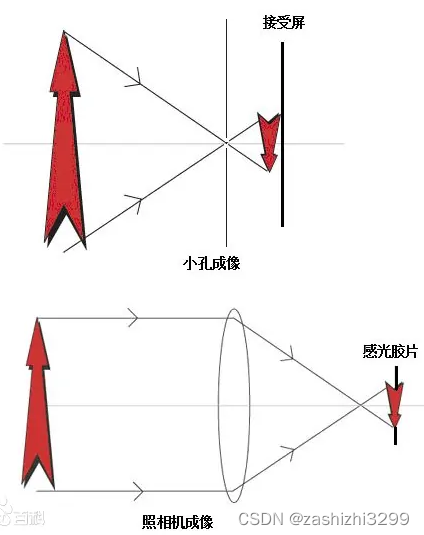
1、理想线性摄像机小孔成像示意图

下图为相机成像。 

如图，小孔成像能否看到倒立的像，取决于物体和孔的距离，以及感光板与孔的距离，按图中公式计算。其中f是焦距。

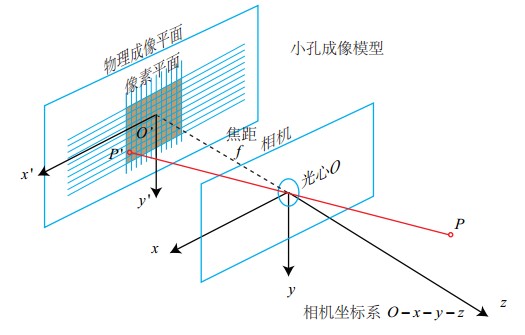
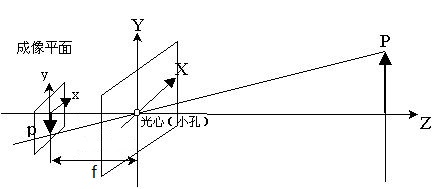
上2个图，为成像模型实际情况，像p与物体P分别位于小孔两侧，且是倒立成像，不利于观看。

2、坐标系转换

坐标转换就是，通过坐标系参数矩阵变换，该用实际物体3D坐标表示2D图片像素点，变换矩阵就是摄像机的内参。

下图，将倒立的像p颠倒并平移到小孔o的另一边，跟实际物体在一边成比例，且为正向，方便画图。

①世界坐标系：是客观三维世界的绝对坐标系，也称客观坐标系。物体实际坐标，用（Xw, Yw, Zw）表示其坐标值。

②相机坐标系（光心坐标系）：以相机的光心（小孔圆心）为坐标原点，X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴，相机的光轴为Z 轴，用（Xc, Yc, Zc）表示其坐标值。

③图像坐标系：以CCD 图像平面的中心为坐标原点，X轴和Y 轴分别平行于图像平面的两条垂直边，用( x , y )表示其坐标值。图像坐标系是用物理单位（例如毫米）表示像素在图像中的位置。

④像素坐标系：以 CCD 图像平面的左上角顶点为原点，X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴，用(u , v )表示其坐标值。数码相机采集的图像首先是形成标准电信号的形式，然后再通过模数转换变换为数字图像。每幅图像的存储形式是M × N的数组，M 行 N 列的图像中的每一个元素的数值代表的是图像点的灰度。这样的每个元素叫像素，像素坐标系就是以像素为单位的图像坐标系。

如下图，是2个坐标系：④像素坐标系uv和③图像坐标系xyimg。

3、张正友标定算法calibration

”张正友标定”是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。文中提出的方法介于传统标定法和自标定法之间，但克服了传统标定法需要的高精度标定物的缺点，而仅需使用一个打印出来的棋盘格就可以。同时也相对于自标定而言，提高了精度，便于操作。因此张氏标定法被广泛应用于计算机视觉方面。

标定参数包括内参和外参。内参表示相机本身参数，外参表示拍摄每一张照片时的相机位置姿态等外部参数。

传统标定

下图，已知拍好的照片和实际物体的3D坐标，反推相机参数。需要的高精度标定物。

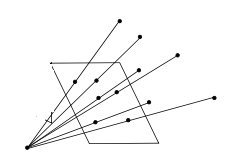
张氏标定步骤

• 打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上
• 对棋盘格拍摄若干张图片（一般10-20张）
• 在图片中检测特征点（Harris特征）
• 利用解析解估算方法计算出5个内部参数，以及6个外部参数
• 根据极大似然估计策略，设计优化目标并实现参数的refinement改善

张氏标定原理

1、成像数学模型表示

图片二维点，真实三维点。增广向量，，摄像机用小孔成像得到3维M到2维m的投影公式：

s是任意比例因子，[R，t]为外部参数：旋转矩阵和位移矩阵。A为相机内部参数矩阵，α和β是图像轴（焦距）的比例因子，γ是两个图像轴之间（传感器轴和光轴）的夹角（当安装准确时γ=0），(u0,v0)是2D图像的中心点。

假设M在坐标轴z=0上，上面的投影公式改写为：

 M可以改写为，所以三维点M和二维点m可以通过3*3单应性矩阵H（Homography matrix）描述：

单目相机的PnP问题。已知物体3D坐标，和图片2D坐标，相机内参已知，求解相机外参，也就是相机的位姿的问题。

4、畸变参数确定

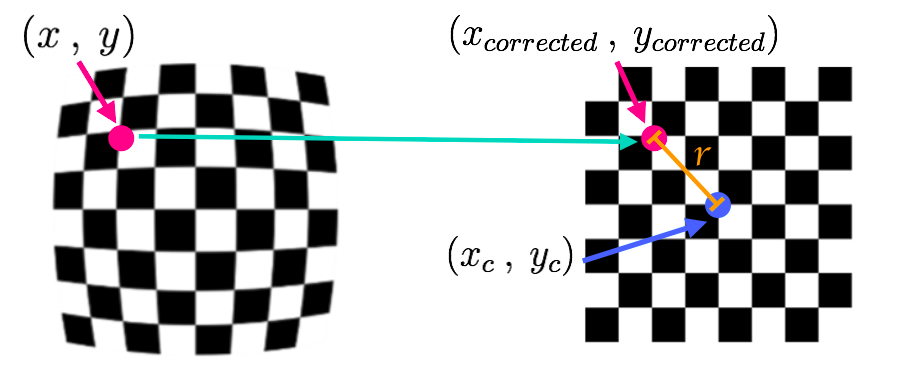
径向畸变系数为k1, k2, k3，切向畸变系数为p1, p2，可以通过如下两个方程求得：

径向畸变计算方程：

切向畸变计算方程：

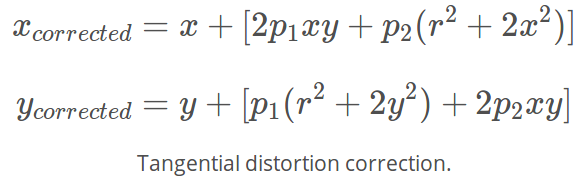
2D点和3D点的变换

• 投影变换：8自由度，将图像转换为不同的投影
• 仿射变换：6自由度，转换将保留原图像平行线的图像
• 相似变换：4自由度，旋转和缩放原图像
• 欧几里得变换：3自由度，旋转原图像

下图为2D和3D的变换等级，矩阵，自由度等

齐次坐标

齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。

在一个2D笛卡尔坐标末尾加上一个额外的变量w来形成2D齐次坐标，因此，一个点(X,Y)在齐次坐标里面变成了(x,y,w)，并且有X = x/w，Y = y/w。

使用齐次坐标，可以表示平行线在透视空间的无穷远处交于一点。欧式坐标无法表示。

例如，笛卡尔坐标系下（1，2）的齐次坐标可以表示为（1，2，1），如果点（1，2）移动到无限远处，它的齐次坐标表示为（1，2，0），在笛卡尔坐标下它变为(∞,∞)，因为(1/0, 2/0) = (∞,∞)。

单应矩阵H(Homography)

单应矩阵约束了同一3D空间点在两个像素平面的2D齐次坐标。例如，两个相机对同一物体拍照，通过相机参数和单应矩阵能互相推算。

用公式表示：

即：

符号表示单应矩阵H约束了qa和qb同方向，但没有约束尺度大小。可通过叉乘消去齐次的尺度因子：,

再通过两个相机的外参旋转平移（R,t），和两个相机的内参K1、K2，和3D点所在平面参数法向量和距离（n，d），计算单应矩阵：

单应矩阵应用举例：将第2个图片放入第1个图片的广告版中

参考文献：

1、从零开始一起学习SLAM | 相机成像模型 - electech6的博客 - CSDN博客  https://blog.csdn.net/electech6/article/details/83617892

2、SLAM入门之视觉里程计(2)：相机模型（内参数，外参数） - Brook_icv - 博客园  https://www.cnblogs.com/wangguchangqing/p/8126333.html

3、【3D视觉工坊】第二期公开课：相机标定的基本原理与经验分享_哔哩哔哩_bilibili  https://www.bilibili.com/video/BV1R7411m7ZQ

4、张正友标定算法原理详解 - 简书  https://www.jianshu.com/p/9d2fe4c2e3b7

5、张正友相机标定法原理与实现_Eating Lee-CSDN博客_张正友标定法原理  https://blog.csdn.net/qq_40369926/article/details/89251296

6、谭平--从相机标定到SLAM，极简三维视觉六小时课程视频_哔哩哔哩_bilibili  https://www.bilibili.com/video/BV124411W775/?p=2&spm_id_from=pageDriver

7、无人驾驶传感器融合系列（十一）—— 相机内参标定_默_存的博客-CSDN博客  https://blog.csdn.net/weixin_40215443/article/details/98478019

8、张正友标定法翻译_heroacool的专栏-CSDN博客_张正友标定法论文  https://blog.csdn.net/heroacool/article/details/50286677

9、《Computer Vision_ Algorithms and Applications-Richard Szeliski》第二章 image formation

10、单应矩阵的推导与理解 - 知乎  https://zhuanlan.zhihu.com/p/138266214

11、图像处理之理解Homography matrix(单应性矩阵) - 云+社区 - 腾讯云  https://cloud.tencent.com/developer/article/1084332

12、

13、

14、

15、