运放反相比例放大电路中反馈电阻两端经常并联一个电容,而运放积分电路的反馈电容上常常并联一个电阻,两者电路结构相似,如下所示(隐去阻容值),二者有何区别呢?电阻、电容分别又起到什么作用?
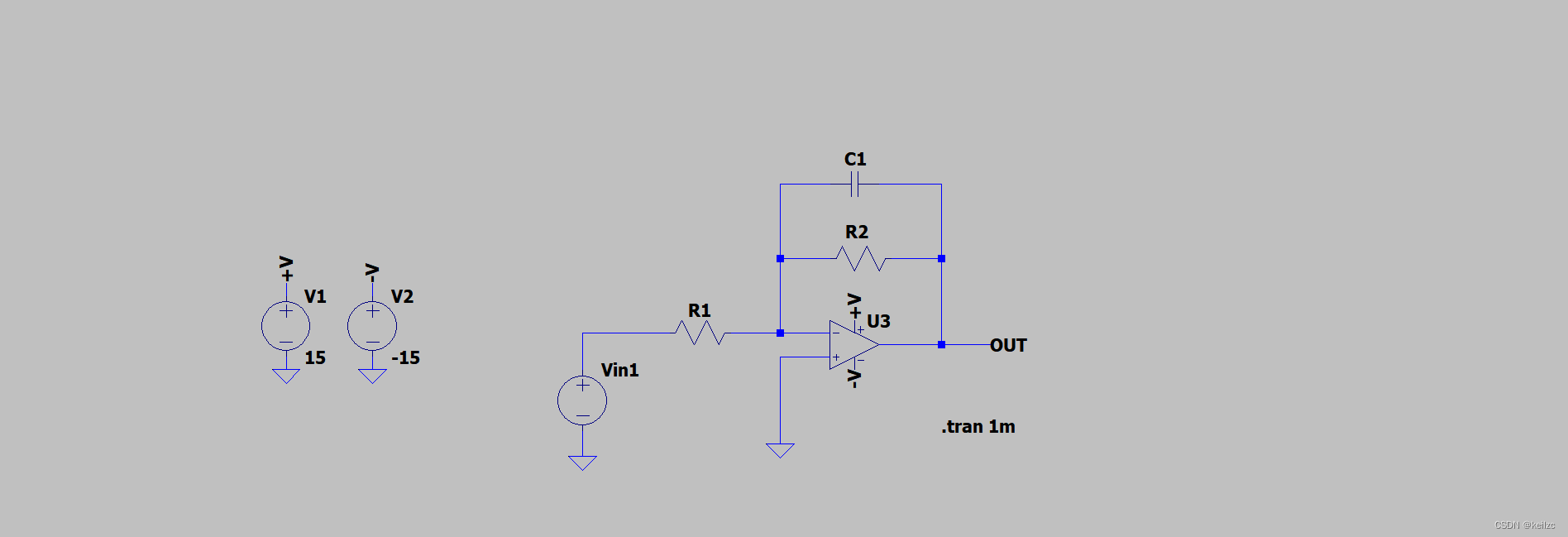
反相放大电路:电阻为主,电容为辅。
先说结论,反相放大电路中,电阻为主,电容为辅,加上电容只是为了让电路更加稳定,避免高频干扰。
从时域角度理解:
我们在LTspice中搭建如下仿真电路,输入端Vin1模拟一个脉冲干扰,观察输出波形vout会怎样?
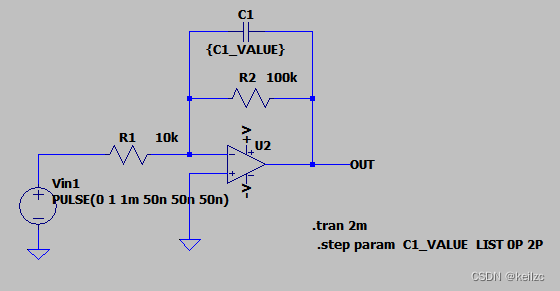
简单介绍:输入信号给1个激励脉冲,初始电平为0V,高电平为1V,1ms时刻开始上升,上升时间为50ns,高电平维持50ns,下降沿50ns。电阻R1为10k,电阻R2为100k,反馈电容设置为可变量C1_VALUE。仿真命令中将C1_VALUE设置为列表形式,取值依次为0pf和2pf,分别对应没有反馈电容和2pf反馈电容,对应的仿真输出曲线也有两条。
仿真结果如下:
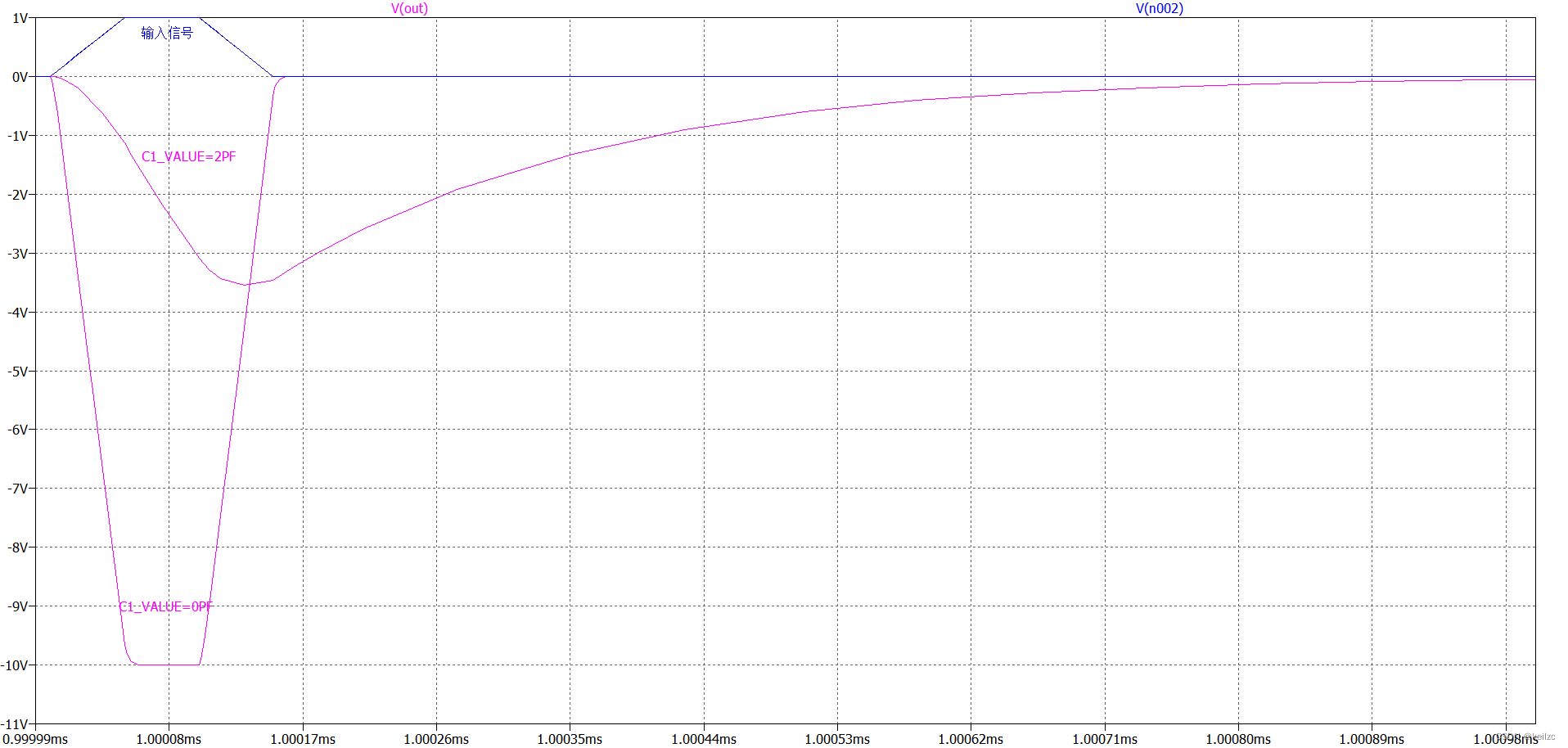
蓝色线为输入信号,模拟1个向上的脉冲信号,上升时间为50ns,高电平为1V,维持50ns,下降沿50ns;
红色线(下面那条,C1_VALUE=0PF)为电容为0pf(即没有电容)时的输出,由图可见当没有反馈电容时,输入信号被反向放大10倍,幅度达到-10V;
红色线(中间那条,C1_VALUE=2PF)为电容为2pf时的输出,由图可见当有反馈电容时,输入信号也会被放大。但由于电容两端电压不能突变,输出电压并不是跟随输入立刻达到-10V,而是缓慢增大。还未达到最大值时,输入信号的脉冲干扰已经消失,此时输出电压不再增加,而是反向减小,恢复原值。与电容滤波原理一样。
电容滤波作用可查考一文彻底讲透电容 【3】—— 电容滤波,不是什么波都能滤的
下面再来另外一种解释方法,参考运放反馈电阻上并联一个小电容有什么作用?它积分运算放大器上的那个反馈电容一样吗?个人觉得并不严谨,也可能是自己理解不够。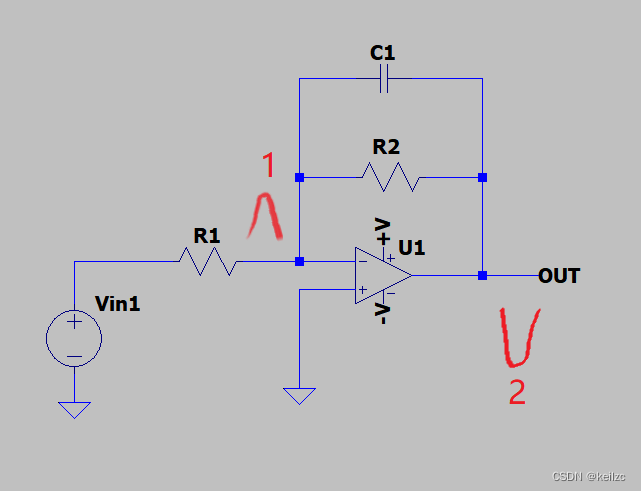
假设输入信号Vin有个向上的脉冲干扰,该干扰传递到运放反相输入端,方向向上;而同相输入端接地,电压不变(由于时间很快,还未建立负反馈,因此虚短还未建立,即同相输入端和反相输入端电压并不一致)。由于运放放大作用此时输出端Vout有个向下脉冲干扰。但是因为有并联电容C1,电容两端电压不能突变,因此电容右端是缓慢向下变化的,与LTspice仿真图中类似。
以上通过仿真和电容知识分析了当有高频干扰时,电容可以起到“缓冲”的作用,减少干扰。
从频域角度理解:
R2、C1 共同组成反馈网络,确切说是“阻抗”,即二者并联值,运放的放大倍数由反馈“阻抗”决定,完整表达式为R2/((1+jwC1R2)*R1)。
对于直流信号而言,w为0(反馈电容阻抗1/jwC1无穷大,相当于开路),此时只有反馈电阻R1有作用,放大倍数退化为R2/R1;对于高频信号,w很大(反馈电容阻抗1/jwC1无穷小,相当于短路),放大倍数趋近于0,即滤除了高频信号,提高运放的稳定性,防止自激震荡。
仿真原理图如下:
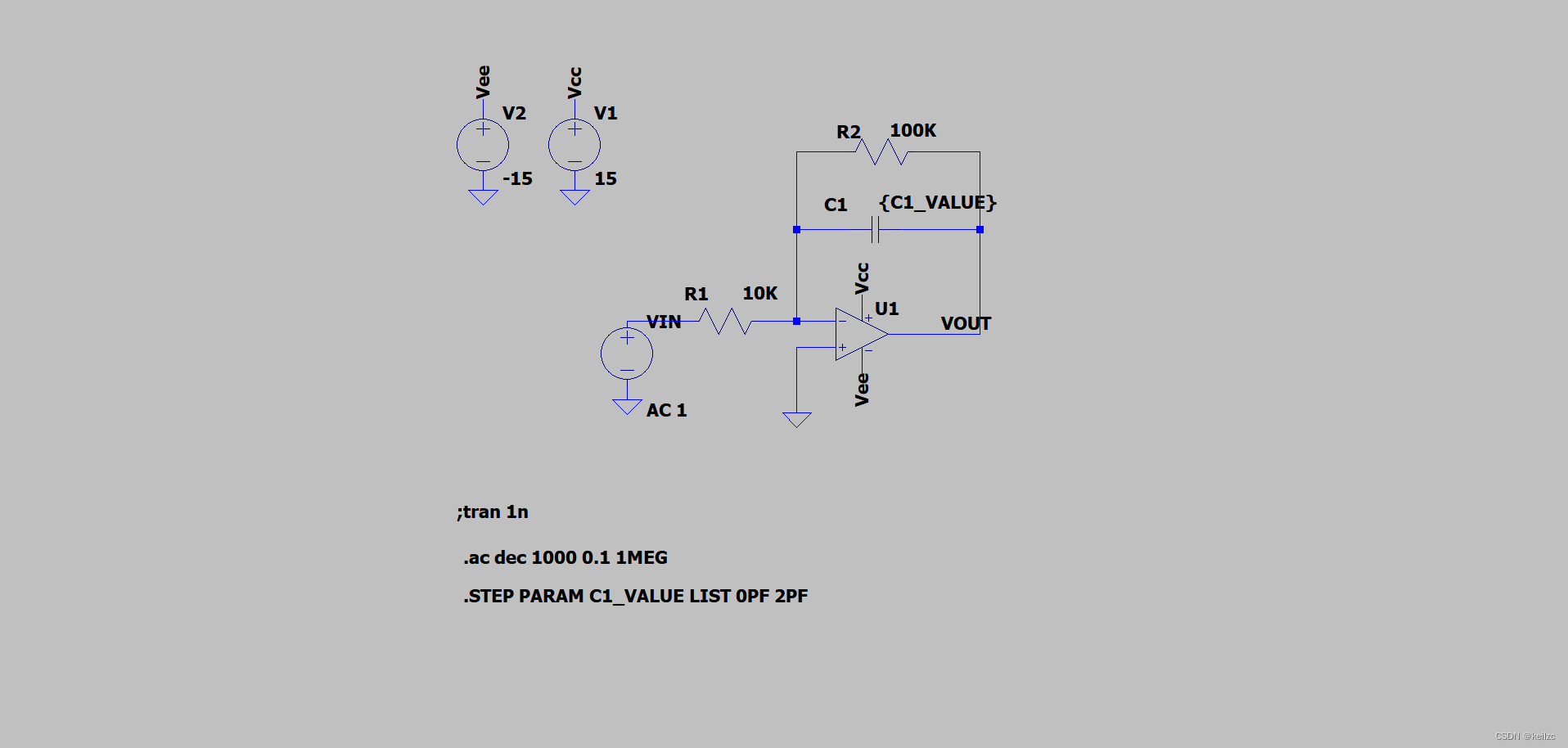
简单介绍:幅频特性仿真,R1为10k,R2为100k,反馈电容设置为可变量C1_VALUE。仿真命令中将C1_VALUE设置为列表形式,取值依次为0pf和2pf,对应的仿真输出曲线也有两条。
仿真结果如下:
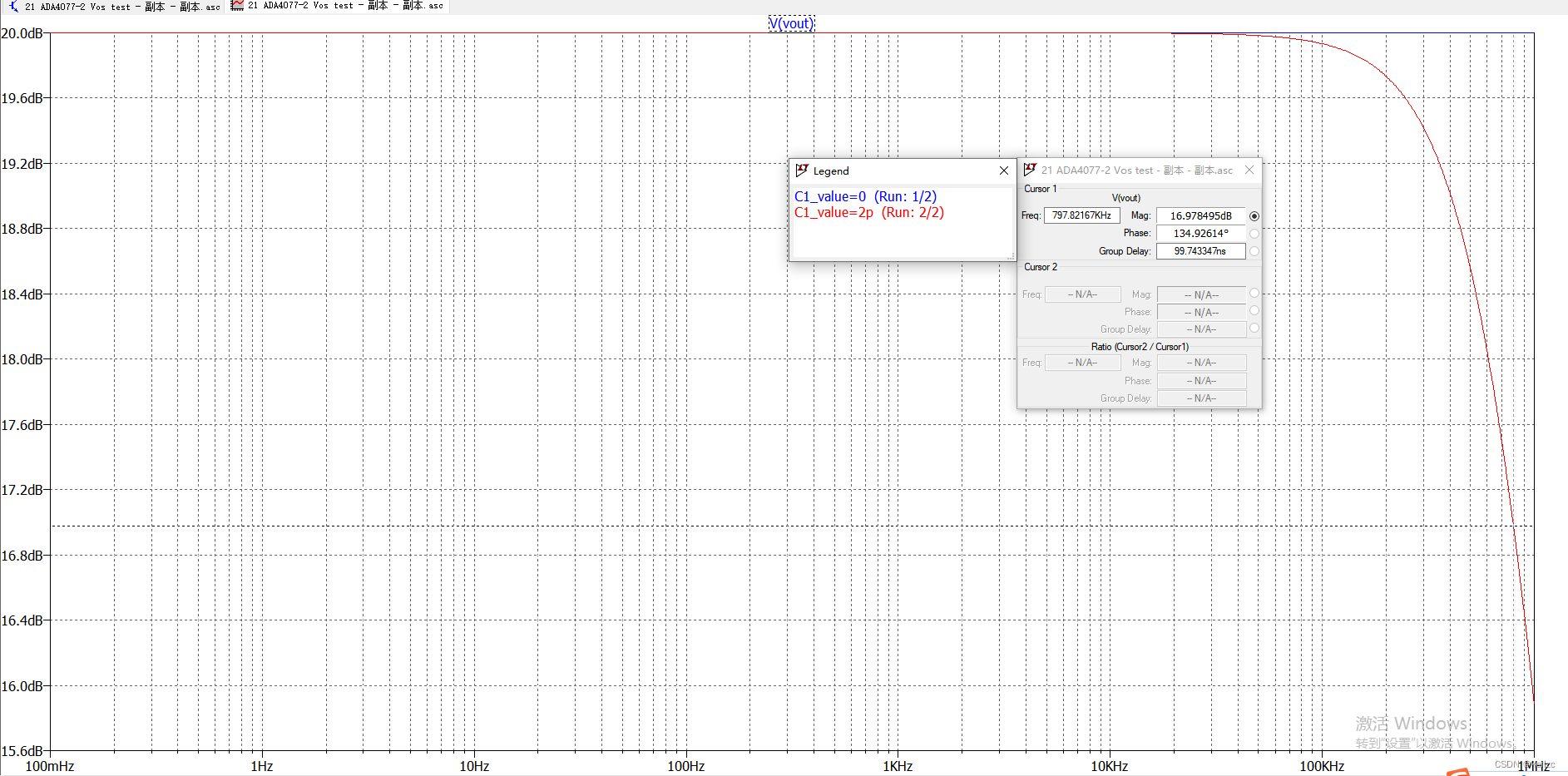
当反馈电容为0pf时,幅频特性曲线如蓝色线条所示,始终为20dB,即放大倍数为100k/10k=10倍。
当反馈电容为2pf时,幅频特性曲线如红色线条所示,呈低通滤波特性:低频段为20dB,随着频率上升增益下降,-3dB大约在797kHz,即1/(2piR2*C1)≈795kHZ,理论值与仿真结果一致。
小结
以上为理想运放仿真结果,实际上由于寄生电容的存在,高频干扰更容易造成电路不稳定。因此,为了提高运放的稳定性,防止自激震荡,可以适当增加反馈电容。反馈电容会改变相位并降低带宽,一般都是选pF级的电容,即电阻为主,电容为辅。
积分电路:电容为主,电阻为辅。
先说结论,运放积分电路中,电容为主,电阻为辅。加上电阻只是为了增加直流通路,避免输入失调电压、输入偏置电流等造成的持续电流使得运放进入饱和状态。
这里贴上《新概念电路》中积分器知识。
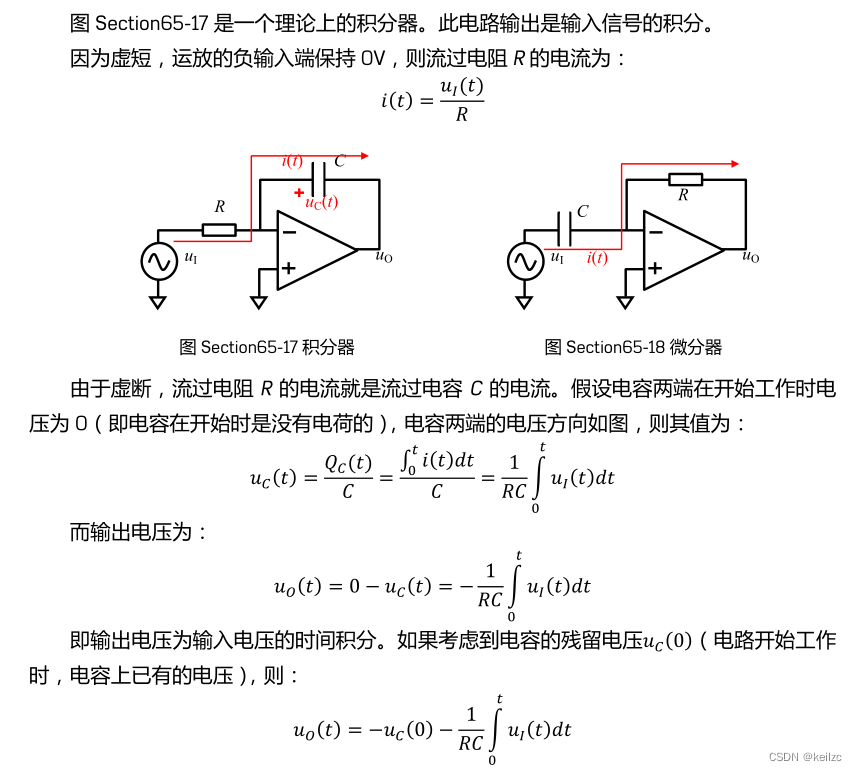

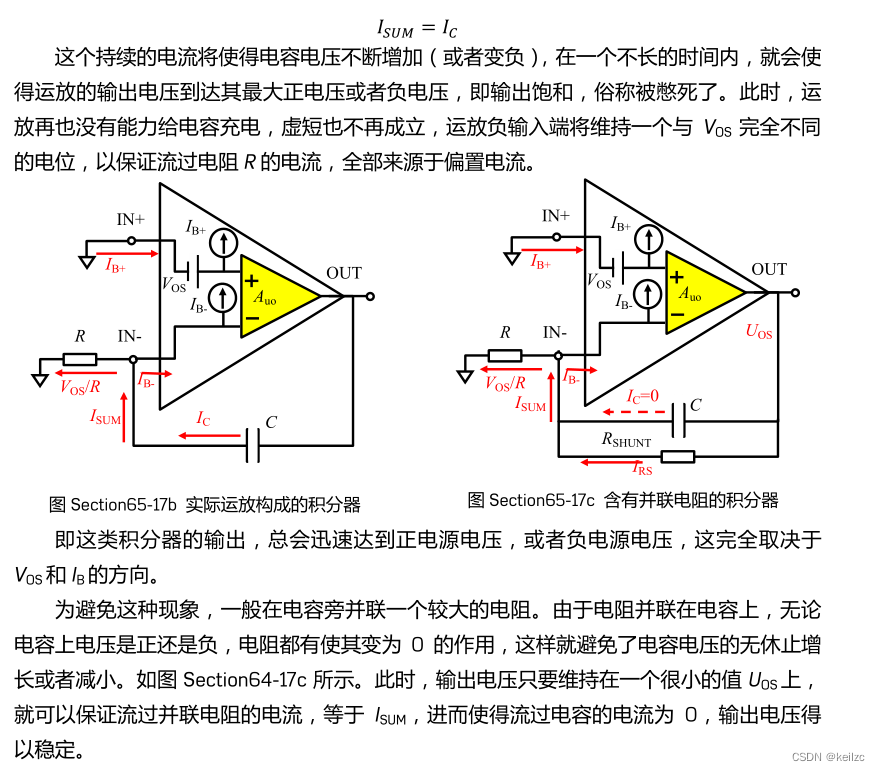
《新概念模拟电路》中已经讲得很清楚,我们这里做个仿真,原理图如下:
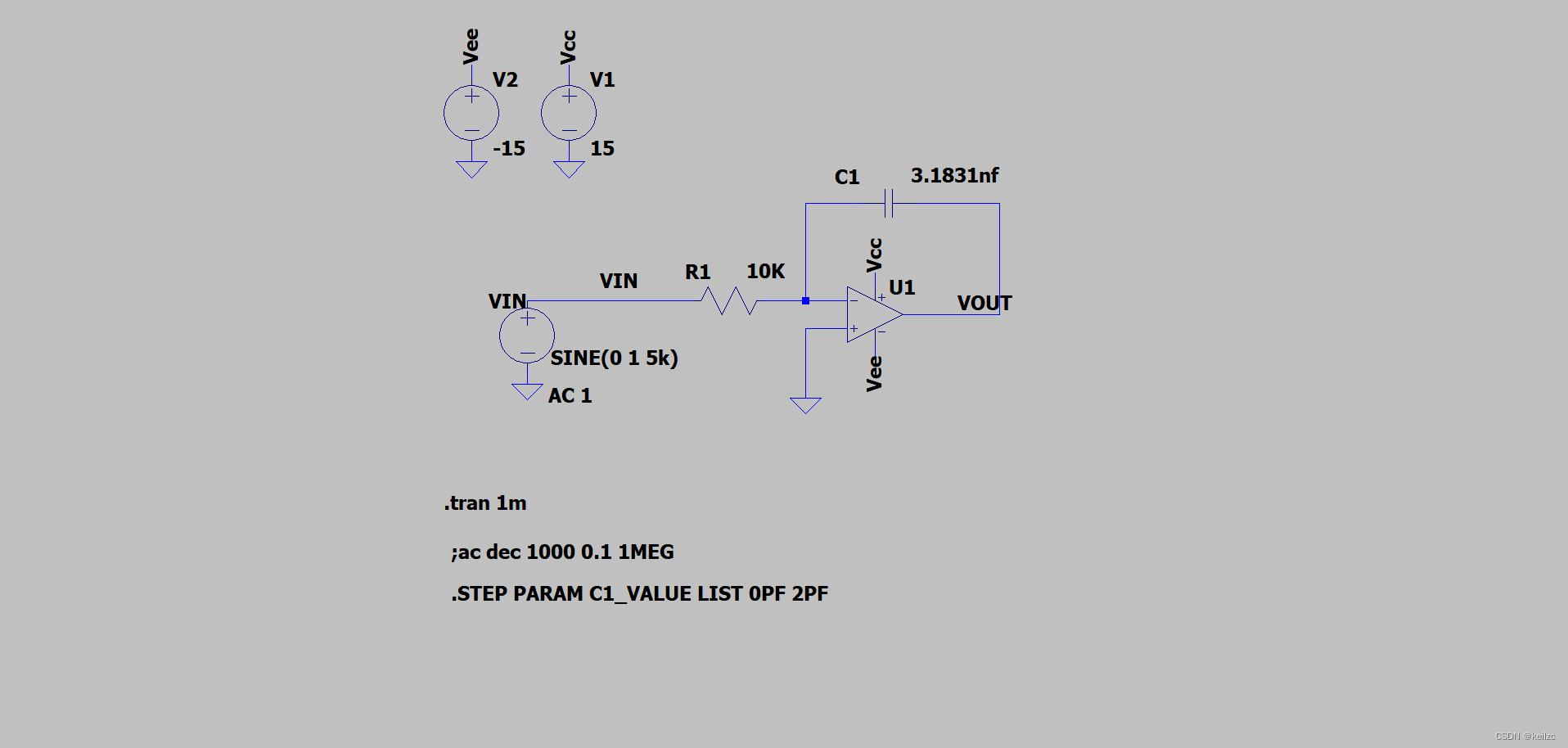
简单介绍:输入信号VIN设置为幅度1V,频率为5kHz的正弦信号。为了便于计算,电容C1设置为3.1831nf,即在5kHz频率下10k阻抗对应的电容值。运放为理想运放。
仿真结果如下:
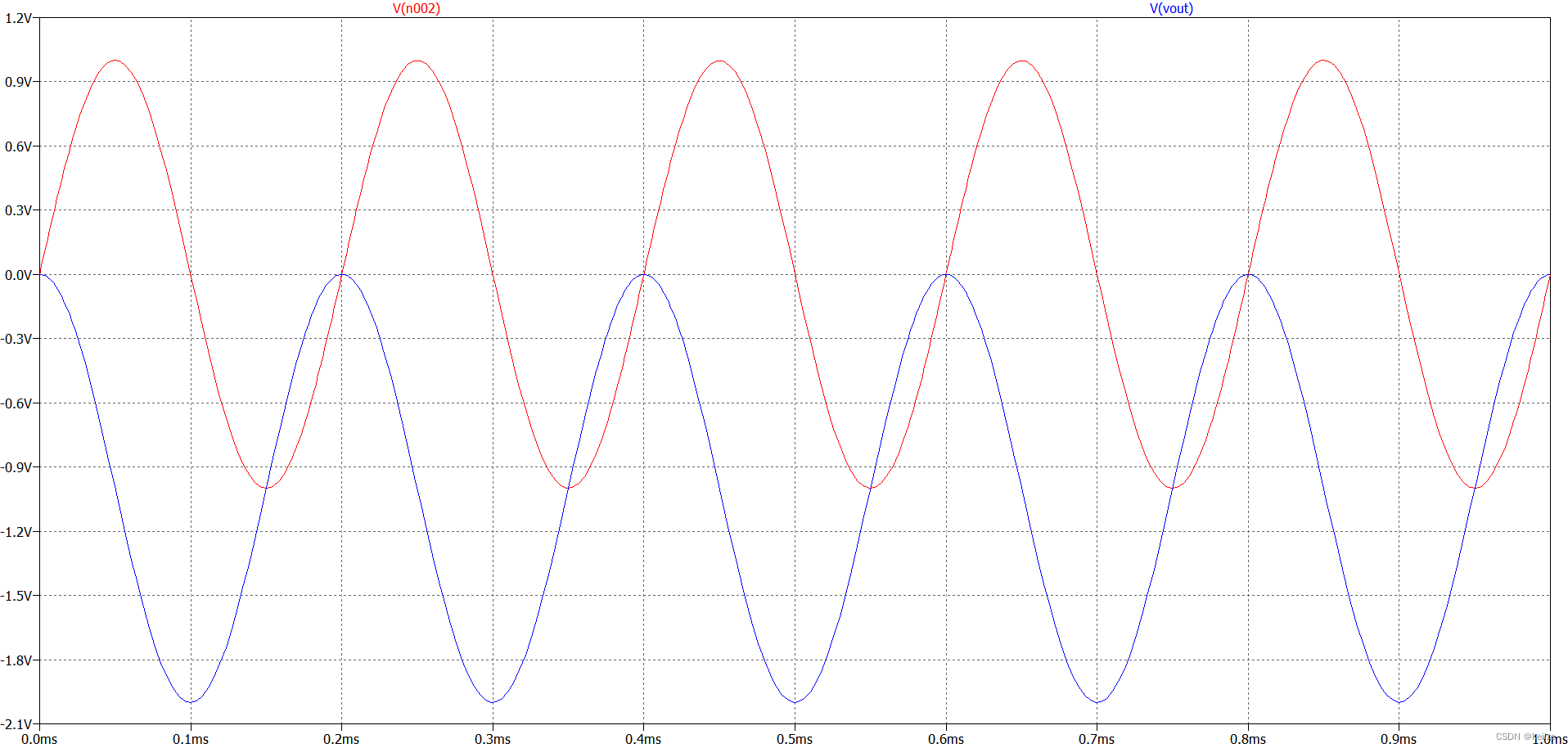
红色为输入信号,幅度为1V,频率为5kHz,蓝色为输出信号,幅度也为1V,频率为5kHz,且输出信号明显为输入信号的积分,即该积分电路可正常工作。
上面为理想情况,实际工作中输入信号可能含有直流成分,运放存在失调电压和失调电流,无论那种情况都会使运放很快进入饱和状态,即输出接近±供电电压。
下面我们调整运放的参数失调电压为1V(实际一般为uV级到mV级,此处为了便于显示,修改为1V),仿真结果如下:
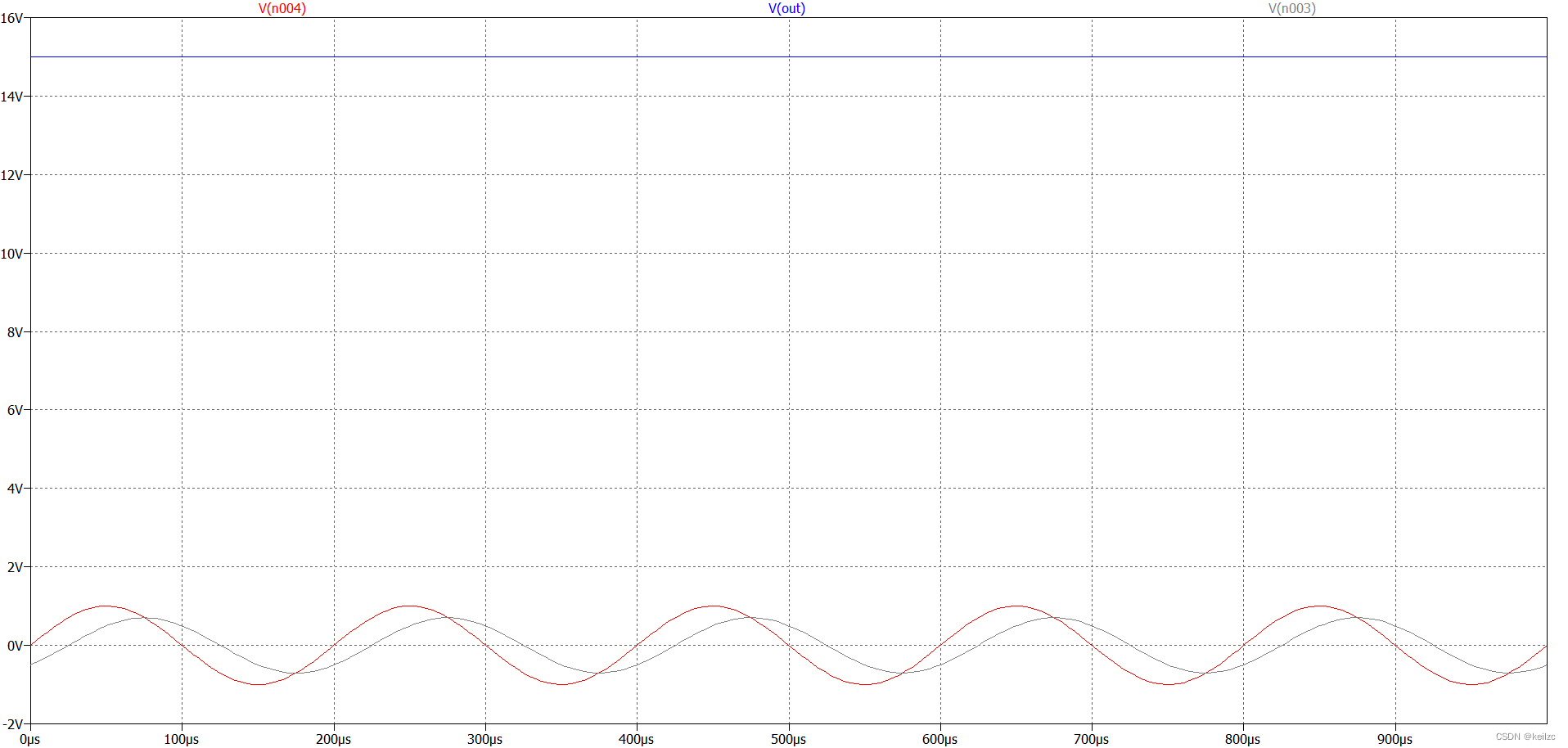
红色为输入信号,交流幅度为1V,频率为5kHz,蓝色为输出信号,趋近于﹣15V,即此时处于饱和状态。根据《新概念》,由于存在直流分量,一直对电容充电,这个时候运放无法维持虚短。图中,灰色线即为运放反相输入端电压,确实不为0,并没有和同相输入端的GND保持一致。
为了使积分电路能正常工作,电容两端并联一个电阻,本次仿真取100k,仿真结果如下:
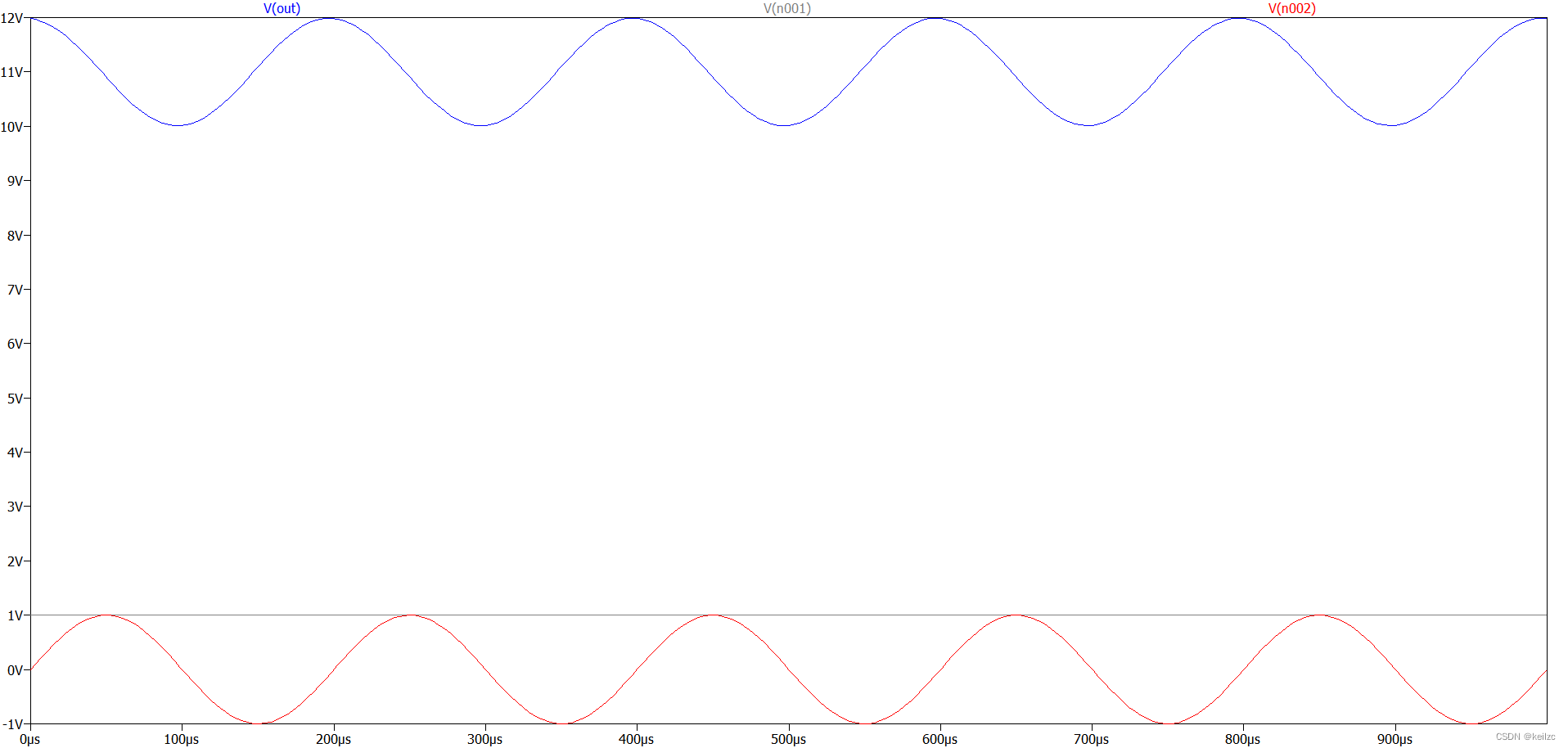
红色为输入信号,交流幅度为1V,频率为5kHz,蓝色为输出信号,均值为-10V,交流幅度为1V,频率为5kHz。灰色线即为运放反相输入端电压,为1V,与我们之前设置的失调电压1V相等,此时满足虚短。由图可见,输出信号为输入信号的积分,只不过多了个直流分量,相当于积分时的常量。本例中失调电压最终放大了10倍,实际使用时失调电压较小,对最终的输出影响也较小。
因此我们可以选取一个合适的电阻值,使积分电路可以正常工作,避免快速进入饱和状态。
也可以换个角度考虑,对于直流信号而言,电容阻抗无穷大,即没有反馈回路,那么运放同相输入端和反相输入端的压差肯定会使运放饱和。增加直流反馈通路后,对于直流信号,该电阻可以形成负反馈回路,避免运放饱和。而对于高频信号而言,电容阻抗较小,只要电阻不选得太小,此时并联阻抗取决于电容,电阻也不会影响电路额高频特性。
小结
为了避免积分电路进入饱和状态,需要增益一条直流反馈回路,确保运放工作在“深度负反馈区”,维持运放的虚短特性,此时积分器才可以正常工作。电阻的选取需要根据实际情况进行分析。





