分析：

考场上看都没看的题。。。但实现起来居然异常简单（相对于隔壁D题动态点分治而言）。。。。

这题除了利用了仙人掌图的定义。。其它都和仙人掌没关系。。。

先考虑一个相对简单的问题：

如果给的是棵树，怎么求答案？

树的性质无非就是两点间路径唯一，也就是说，这里的“最大流”可以看作两点间路径上的边权最小值。

从大到小加入边。每次加入时，因为两端点所在的联通块中，这条边边权一定是最小的（比它边权小的边都还没加入）。那么这两个联通块之间的路径最小值一定可以在当前这条边上取到。所以就可以算出这条边对最终答案的贡献。

由于题目非常鬼畜地要异或点的编号，所以这里求贡献还是需要一点技巧：

用并查集维护每个点所在的联通块中，编号在二进制下第$k$位为0、为1的点的数量，设为$sum_{k0}$和$sum_{k1}$。

我们可以按边权在二进制下的每一位，分别求贡献。

若边权二进制下第$i$位为1，那么就要求两个点的编号在第$i$位的值必须相同（否则xor之后就是0了），
这部分的贡献就是$(sum_{i0}(u) *sum_{i0}(v)+sum_{i1}(u)*sum_{i1}(v))*2^i$

若边权二进制下第$i$位为0，那么就要求两个点的编号在第$i$位的值必须不同

这部分的贡献就是$(sum_{i0}(u) *sum_{i1}(v)+sum_{i1}(u)*sum_{i0}(v))*2^i$

仙人掌图如何求答案？

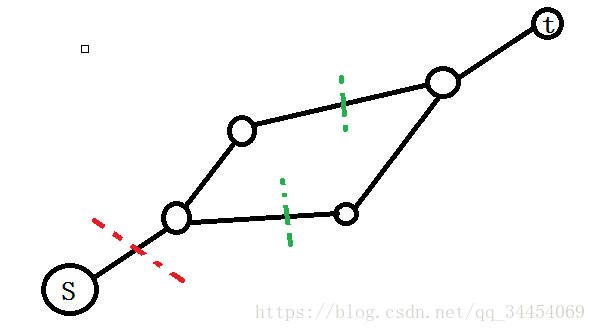
这里又要利用最小割最大流定理了，找两个点之间的最大流，无非就是在这两个点之间找一条最小割。结合仙人掌图的定义：每条边最多出现在一个简单环中。那么最小割只有两种情况：删去某个环上的两条边、或删去一条树边（即不在简单环上的边）。

而且如果删去环上的边，必然会删去这个环上边权最小的一条。

那么可以把每个环上边权最小的边删去，然后把其余的边全部加上这条边的权值即可。因为割去这个环上任意一条边，都会割去最小边，那么可以直接把最小边的代价加到其他边里面去，然后删去最小边。

由于每条边最多在一个简单环里，所以这里的加权操作可以直接暴力搞。

这个骚操作之后，这个图就变成一颗树了。。。。然后就可以按照上面的做法过掉了。。。

这题数据范围卡得很好啊。。unsigned long long 才能过。。。是不是考场上很多人被这个坑了所以过的人不多？

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define SF scanf
#define PF printf
#define MAXN 300010
using namespace std;
typedef unsigned long long ull;
ull ans=0;
int cnt;
int fa[MAXN];
ull siz[MAXN][32][2];
struct node{int u,v;int val;node () {}node (int u1,int v1,int val1):u(u1),v(v1),val(val1) {}bool operator < (const node &a) const {return val>a.val;}
}l[MAXN];
int dep[MAXN],fai[MAXN],soi[MAXN];
vector<int> a[MAXN];
vector<ull> w[MAXN];
bool used[MAXN];
void dfs(int x,int f,int id){dep[x]=dep[f]+1;soi[x]=id;for(int i=0;i<a[x].size();i++){int u=a[x][i];if(u==f){fai[x]=i;continue;}dfs(u,x,i);}   
}
void add(int x,int y,int val){if(x==y)return ;if(dep[x]<dep[y])swap(x,y);while(dep[x]!=dep[y]){int f=a[x][fai[x]];w[x][fai[x]]+=val;w[f][soi[x]]+=val;x=f;}while(x!=y){int f=a[x][fai[x]];w[x][fai[x]]+=val;w[f][soi[x]]+=val;x=f;f=a[y][fai[y]];w[y][fai[y]]+=val;w[f][soi[y]]+=val;y=f;}
}
void dfs1(int x,int f){for(int i=0;i<a[x].size();i++){int u=a[x][i];if(u==f)continue;l[++cnt]=node(x,u,w[x][i]);dfs1(u,x);}
}
int get_fa(int x){if(fa[x]==0)return x;fa[x]=get_fa(fa[x]);return fa[x];   
}
void merge(int x,int y,int val){x=get_fa(x);y=get_fa(y);for(ull i=0;i<31;i++){if(val&(1ull<<i)){ans+=siz[x][i][0]*siz[y][i][0]*(1ull<<i);ans+=siz[x][i][1]*siz[y][i][1]*(1ull<<i);}else{ans+=siz[x][i][0]*siz[y][i][1]*(1ull<<i);ans+=siz[x][i][1]*siz[y][i][0]*(1ull<<i);}}fa[x]=y;for(int i=0;i<31;i++){siz[y][i][0]+=siz[x][i][0];siz[y][i][1]+=siz[x][i][1];}
}
int main(){//freopen("1001.in","r",stdin);//freopen("1.txt","w",stdout);int t;SF("%d",&t);while(t--){int n,m;SF("%d%d",&n,&m);for(int i=1;i<=n;i++){fa[i]=0;dep[i]=0;   for(int j=0;j<31;j++){siz[i][j][0]=((i>>j)&1)^1;siz[i][j][1]=((i>>j)&1);}a[i].clear();w[i].clear();}for(int i=1;i<=m;i++){SF("%d%d%d",&l[i].u,&l[i].v,&l[i].val);used[i]=0;}sort(l+1,l+1+m);for(int i=1;i<=m;i++){int fu=get_fa(l[i].u);int fv=get_fa(l[i].v);if(fu!=fv){used[i]=1;fa[fu]=fv;a[l[i].u].push_back(l[i].v);a[l[i].v].push_back(l[i].u);w[l[i].u].push_back(l[i].val);w[l[i].v].push_back(l[i].val);}}dfs(1,0,0);for(int i=1;i<=n;i++)fa[i]=0;for(int i=1;i<=m;i++)if(used[i]==0)add(l[i].u,l[i].v,l[i].val);cnt=0;dfs1(1,0);sort(l+1,l+n);ans=0;for(int i=1;i<n;i++)merge(l[i].u,l[i].v,l[i].val);PF("%llu\n",ans);}
}