文章目录
- 一、初始基可行解后第一次迭代
- 二、迭代后新的单纯形表
- 三、方程组同解变换
- 四、生成新的单纯形表
- 五、解出基可行解
- 六、计算检验数 σ j \sigma_j σj 并选择入基变量
- 七、计算 θ \theta θ 值并选择出基变量
上篇博客 【运筹学】线性规划数学模型 ( 单纯形法 | 迭代原则 | 入基 | 出基 | 线性规划求解示例 ) 讲解了单纯形法中选择了入基变量 , 与出基变量 , 找到了下一组迭代的可行基 , 下面开始继续进行后续操作 ;
一、初始基可行解后第一次迭代
线性规划标准形式为 :
m a x Z = 3 x 1 + 4 x 2 + 0 x 3 + 0 x 4 { 2 x 1 + x 2 + x 3 + 0 x 4 = 40 x 1 + 3 x 2 + 0 x 3 + x 4 = 30 x j ≥ 0 ( j = 1 , 2 , 3 , 4 ) \begin{array}{lcl} max Z = 3x_1 + 4x_2 + 0x_3 + 0x_4 \\ \\ \begin{cases} 2 x_1 + x_2 + x_3 + 0x_4 = 40 \\\\ x_1 + 3x_2 + 0x_3 + x_4 = 30 \\\\ x_j \geq 0 & (j = 1 , 2 , 3 , 4 ) \end{cases}\end{array} maxZ=3x1+4x2+0x3+0x4⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧2x1+x2+x3+0x4=40x1+3x2+0x3+x4=30xj≥0(j=1,2,3,4)
选择初始基可行解并验证最优解 : 选择初始基可行解经过验证 , 不是最优解 , 该初始基可行解对应基变量是 x 3 , x 4 x_3,x_4 x3,x4 ;
进行迭代 : 开始进行迭代 , 选择 x 2 x_2 x2 作为入基 , 选择 x 4 x_4 x4 作为出基 , 新的基变量变成了 x 3 , x 2 x_3 , x_2 x3,x2 , 新的基矩阵变为 [ 1 1 0 3 ] \begin{bmatrix} &1 & 1 & \\\\ &0 & 3 & \end{bmatrix} ⎣⎡1013⎦⎤ ;
二、迭代后新的单纯形表
单纯形表中的矩阵要求 : 单纯形表中的矩阵是特殊形式的矩阵 , 基矩阵对应的矩阵必须是单位阵 , 非基矩阵对应的矩阵是 B − 1 N B^{-1}N B−1N ;
只要基矩阵变换为单位阵 , 非基矩阵自然就是 B − 1 N B^{-1}N B−1N
参考 : 【运筹学】线性规划数学模型 ( 单纯形法 | 最优解判定原则 | 单纯形表 | 系数计算方法 | 根据系数是否小于等于 0 判定最优解 ) 四、 B − 1 N B^{-1}N B−1N 分析
同解方程组 : 同一个线性规划 , 方程组的解不能变 ;
方程组同解变换 : 保证同解方程组前提下 , 使 x 2 x_2 x2 对应的列向量由 ( 1 3 ) \begin{pmatrix} \quad 1 \quad \\ \quad 3 \quad \end{pmatrix} (13) 变成 ( 0 1 ) \begin{pmatrix} \quad 0 \quad \\ \quad 1 \quad \end{pmatrix} (01) , 这样 x 3 x_3 x3 与 x 2 x_2 x2 对应的列向量组成的基矩阵就变成了 ( 1 0 0 1 ) \begin{pmatrix} \quad 1 \quad 0 \quad \\ \quad 0 \quad 1 \quad \end{pmatrix} (1001) , 此时基变量是单位阵 , 非基矩阵自然就是 B − 1 N B^{-1}N B−1N ;
三、方程组同解变换
方程组做同解变换 :
线性规划原始方程组为 { 2 x 1 + x 2 + x 3 + 0 x 4 = 40 x 1 + 3 x 2 + 0 x 3 + x 4 = 30 \begin{cases} 2 x_1 + x_2 + x_3 + 0x_4 = 40 \\\\ x_1 + 3x_2 + 0x_3 + x_4 = 30 \end{cases} ⎩⎪⎨⎪⎧2x1+x2+x3+0x4=40x1+3x2+0x3+x4=30 , 需要将 x 2 x_2 x2 的系数变为 ( 0 1 ) \begin{pmatrix} \quad 0 \quad \\ \quad 1 \quad \end{pmatrix} (01) , x 3 x_3 x3 的系数保持 ( 1 0 ) \begin{pmatrix} \quad 1 \quad \\ \quad 0 \quad \end{pmatrix} (10) 不变 ;
方程 2 2 2 同解变换 : 在 x 1 + 3 x 2 + 0 x 3 + x 4 = 30 x_1 + 3x_2 + 0x_3 + x_4 = 30 x1+3x2+0x3+x4=30 中 , 需要将 x 2 x_2 x2 的系数变成 1 1 1 , 在方程两端乘以 1 3 \dfrac{1}{3} 31 , 此时方程变成 1 3 x 1 + x 2 + 0 x 3 + 1 3 x 4 = 10 \dfrac{1}{3}x_1 + x_2 + 0x_3 + \dfrac{1}{3}x_4 = 10 31x1+x2+0x3+31x4=10 ;
方程 1 1 1 同解变换 : 将上述方程 2 2 2 作同解变换后 , 方程组变成 { 2 x 1 + x 2 + x 3 + 0 x 4 = 40 1 3 x 1 + x 2 + 0 x 3 + 1 3 x 4 = 10 \begin{cases} 2 x_1 + x_2 + x_3 + 0x_4 = 40 \\\\ \dfrac{1}{3}x_1 + x_2 + 0x_3 + \dfrac{1}{3}x_4 = 10 \end{cases} ⎩⎪⎪⎨⎪⎪⎧2x1+x2+x3+0x4=4031x1+x2+0x3+31x4=10 , 目前的需求是将方程 1 1 1 的 x 2 x_2 x2 系数变为 0 0 0 , 使用方程 1 1 1 减去 方程 2 2 2 即可得到要求的矩阵 :
( 2 − 1 3 ) x 1 + 0 x 2 + x 3 + ( 0 − 1 3 ) x 4 = 40 − 10 5 3 x 1 + 0 x 2 + x 3 − 1 3 x 4 = 30 \begin{array}{lcl} (2 - \dfrac{1}{3}) x_1 + 0 x_2 + x_3 + (0 - \dfrac{1}{3}) x_4 &=& 40 - 10 \\\\ \dfrac{5}{3} x_1 + 0x_2 + x_3 - \dfrac{1}{3} x_4 &=& 30 \end{array} (2−31)x1+0x2+x3+(0−31)x435x1+0x2+x3−31x4==40−1030
最终方程 1 1 1 转化为 5 3 x 1 + 0 x 2 + x 3 − 1 3 x 4 = 30 \dfrac{5}{3} x_1 + 0x_2 + x_3 - \dfrac{1}{3} x_4 = 30 35x1+0x2+x3−31x4=30 ;
同解变换完成后的方程组为 { 5 3 x 1 + 0 x 2 + x 3 − 1 3 x 4 = 30 1 3 x 1 + x 2 + 0 x 3 + 1 3 x 4 = 10 \begin{cases} \dfrac{5}{3} x_1 + 0x_2 + x_3 - \dfrac{1}{3} x_4 = 30 \\\\ \dfrac{1}{3}x_1 + x_2 + 0x_3 + \dfrac{1}{3}x_4 = 10 \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧35x1+0x2+x3−31x4=3031x1+x2+0x3+31x4=10
四、生成新的单纯形表
单纯形表变成如下形式 : 下面的单纯形表中 , 上面部分是初始基可行解对应的单纯形表 , 下面的部分是本次迭代后生成的新的单纯形表 ;
将同解变换后的方程组中的 系数矩阵 , 和 常数 , 填入新的单纯形表中 ;
| c j c_j cj | c j c_j cj | 3 3 3 | 4 4 4 | 0 0 0 | 0 0 0 | ||
|---|---|---|---|---|---|---|---|
| C B C_B CB 基变量系数 (目标函数) | 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | θ i \theta_i θi |
| 0 0 0 ( 目标函数 x 3 x_3 x3 系数 c 3 c_3 c3 ) | x 3 x_3 x3 | 40 40 40 | 2 2 2 | 1 1 1 | 1 1 1 | 0 0 0 | 40 40 40 ( θ 3 \theta_3 θ3 ) |
| 0 0 0 ( 目标函数 x 4 x_4 x4 系数 c 4 c_4 c4) | x 4 x_4 x4 | 30 30 30 | 1 1 1 | 3 3 3 | 0 0 0 | 1 1 1 | 10 10 10 ( θ 4 \theta_4 θ4 ) |
| σ j \sigma_j σj | 3 3 3 ( σ 1 \sigma_1 σ1 ) | 4 4 4 ( σ 2 \sigma_2 σ2 ) | 0 0 0 | 0 0 0 | |||
| – | – | – | – | – | – | – | – |
| 0 0 0 ( 目标函数 x 3 x_3 x3 系数 c 3 c_3 c3 ) | x 3 x_3 x3 | 30 30 30 | 5 3 \dfrac{5}{3} 35 | 0 0 0 | 1 1 1 | − 1 3 -\dfrac{1}{3} −31 | ? ? ? ( θ 3 \theta_3 θ3 ) |
| 4 4 4 ( 目标函数 x 2 x_2 x2 系数 c 2 c_2 c2) | x 2 x_2 x2 | 10 10 10 | 1 3 \dfrac{1}{3} 31 | 1 1 1 | 0 0 0 | 1 3 \dfrac{1}{3} 31 | ? ? ? ( θ 2 \theta_2 θ2 ) |
| σ j \sigma_j σj ( 检验数 ) | 5 3 \dfrac{5}{3} 35 ( σ 1 \sigma_1 σ1 ) | 0 0 0 | 0 0 0 | − 4 3 -\dfrac{4}{3} −34 ( σ 4 \sigma_4 σ4 ) |
五、解出基可行解
新的 基变量是 x 3 , x 2 x_3 , x_2 x3,x2 , 对应的基矩阵是 ( 1 0 0 1 ) \begin{pmatrix} \quad 1 \quad 0 \quad \\ \quad 0 \quad 1 \quad \end{pmatrix} (1001) , 非基变量是 x 1 , x 4 x_1, x_4 x1,x4 , 对应的非基矩阵是 ( 5 3 − 1 3 1 3 1 3 ) \begin{pmatrix} \quad \dfrac{5}{3} \quad -\dfrac{1}{3} \quad \\ \quad \dfrac{1}{3} \quad \dfrac{1}{3} \quad \end{pmatrix} ⎝⎜⎛35−313131⎠⎟⎞ , 将非基变量设置为 0 0 0 , 方程组为 { 5 3 × 0 + 0 x 2 + x 3 − 1 3 × 0 = 30 1 3 × 0 + x 2 + 0 x 3 + 1 3 × 0 = 10 \begin{cases} \dfrac{5}{3} \times 0 + 0x_2 + x_3 - \dfrac{1}{3} \times 0 = 30 \\\\ \dfrac{1}{3} \times 0 + x_2 + 0x_3 + \dfrac{1}{3} \times 0 = 10 \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧35×0+0x2+x3−31×0=3031×0+x2+0x3+31×0=10 , 解出基变量为 { x 3 = 30 x 2 = 10 \begin{cases} x_3 = 30 \\\\ x_2 = 10 \end{cases} ⎩⎪⎨⎪⎧x3=30x2=10 , 基可行解 为 ( 0 10 30 0 ) \begin{pmatrix} \quad 0 \quad \\ \quad 10 \quad \\ \quad 30 \quad \\ \quad 0 \quad \end{pmatrix} ⎝⎜⎜⎛010300⎠⎟⎟⎞
六、计算检验数 σ j \sigma_j σj 并选择入基变量
根据 【运筹学】线性规划数学模型 ( 单纯形法 | 最优解判定原则 | 单纯形表 | 系数计算方法 | 根据系数是否小于等于 0 判定最优解 ) 博客中分析 , 检验数计算公式为 :
- 矩阵形式 : C N T − C B T B − 1 N C_N^T - C_B^T B^{-1}N CNT−CBTB−1N
- 单个检验数计算公式 : σ j = c j − ∑ c i a i j \sigma_j = c_j - \sum c_i a_{ij} σj=cj−∑ciaij
基变量的检验数是 0 0 0 , 主要是求非基变量的检验数 σ 1 , σ 4 \sigma_1 , \sigma_4 σ1,σ4 ;
σ 1 = c 1 − ( c 3 a 11 + c 2 a 12 ) \sigma_{1} = c_1 - ( c_3 a_{11} + c_2 a_{12} ) σ1=c1−(c3a11+c2a12)
σ 1 = 3 − ( 0 × 5 3 ) − ( 4 × 1 3 ) = 5 3 \sigma_{1} =3 - (0 \times \dfrac{5}{3}) - (4 \times \dfrac{1}{3}) = \dfrac{5}{3} σ1=3−(0×35)−(4×31)=35 , 是从下面的单纯形表中的如下位置提取的数值 ;

σ 4 = c 4 − ( c 3 a 41 + c 2 a 42 ) \sigma_{4} = c_4 - ( c_3 a_{41} + c_2 a_{42} ) σ4=c4−(c3a41+c2a42)
σ 4 = 0 − ( 0 × − 1 3 ) − ( 4 × 1 3 ) = − 4 3 \sigma_{4} =0 - (0 \times -\dfrac{1}{3}) - (4 \times \dfrac{1}{3}) = -\dfrac{4}{3} σ4=0−(0×−31)−(4×31)=−34 , 是从下面的单纯形表中的如下位置提取的数值 ;
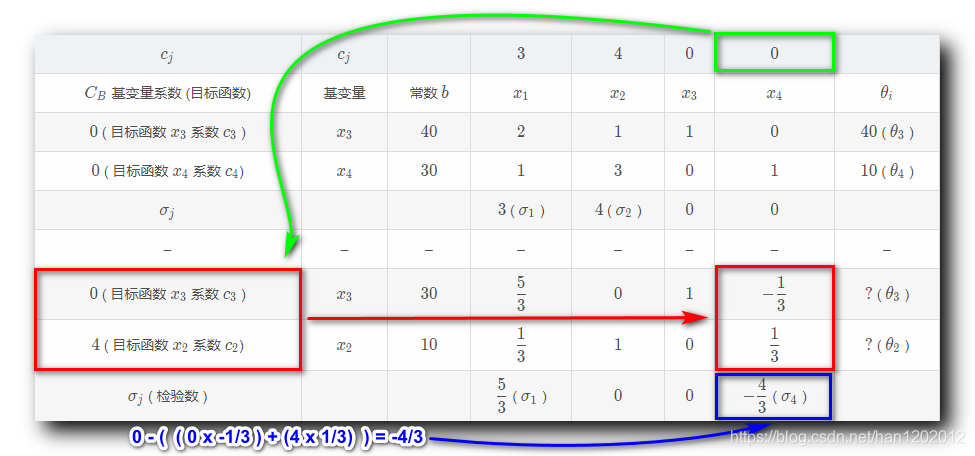
检验数 { σ 1 = 3 − ( 0 × 5 3 ) − ( 4 × 1 3 ) = 5 3 σ 4 = 0 − ( 0 × − 1 3 ) − ( 4 × 1 3 ) = − 4 3 \begin{cases} \sigma_{1} =3 - (0 \times \dfrac{5}{3}) - (4 \times \dfrac{1}{3}) = \dfrac{5}{3} \\\\ \sigma_{4} =0 - (0 \times -\dfrac{1}{3}) - (4 \times \dfrac{1}{3}) = -\dfrac{4}{3} \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧σ1=3−(0×35)−(4×31)=35σ4=0−(0×−31)−(4×31)=−34 , σ 1 \sigma_1 σ1 是大于 0 0 0 的 , 两个检验数必须都小于等于 0 0 0 , 该基可行解才算作是最优解 , 因此 该基可行解不是最优解 ;
根据检验数选择入基变量 : 继续迭代 , 选择检验数较大的非基变量 , 作为入基变量 , 这里入基变量是 x 1 x_1 x1 ;
七、计算 θ \theta θ 值并选择出基变量
参考博客 【运筹学】线性规划数学模型 ( 单纯形法 | 迭代原则 | 入基 | 出基 | 线性规划求解示例 ) 五、出基与入基变量选择
入基变量 根据检验数 σ \sigma σ 选择的是 x 1 x_1 x1 ;
出基变量是根据 θ \theta θ 值来选择的 , 选择 θ \theta θ 值较小的值对应的基变量作为出基变量 ;
θ \theta θ 值计算 : 常数列 b = ( 30 10 ) b =\begin{pmatrix} \quad 30 \quad \\ \quad 10 \quad \end{pmatrix} b=(3010) , 分别除以除以入基变量 x 1 x_1 x1 大于 0 0 0 的系数列 ( 5 3 1 3 ) \begin{pmatrix} \quad \dfrac{5}{3} \quad \\\\ \quad \dfrac{1}{3} \quad \end{pmatrix} ⎝⎜⎜⎛3531⎠⎟⎟⎞ , 计算过程如下 ( 30 5 3 10 1 3 ) \begin{pmatrix} \quad \cfrac{30}{\dfrac{5}{3}} \quad \\\\ \quad \cfrac{10}{\dfrac{1}{3}} \quad \end{pmatrix} ⎝⎜⎜⎜⎜⎜⎜⎜⎛35303110⎠⎟⎟⎟⎟⎟⎟⎟⎞ , 得出结果是 ( 18 30 ) \begin{pmatrix} \quad 18 \quad \\\\ \quad 30 \quad \end{pmatrix} ⎝⎛1830⎠⎞ , 然后选择一个最小值 18 18 18 , 查看该最小值对应的变量是 x 3 x_3 x3 , 选择该变量作为出基变量 ;

x 1 x_1 x1 作入基变量 , x 3 x_3 x3 作出基变量 ; 使用 x 1 x_1 x1 替代基变量中 x 3 x_3 x3 的位置 ;
迭代后的基变量为 x 1 , x 2 x_1 ,x_2 x1,x2 ;
更新一下单纯形表 :
| c j c_j cj | c j c_j cj | 3 3 3 | 4 4 4 | 0 0 0 | 0 0 0 | ||
|---|---|---|---|---|---|---|---|
| C B C_B CB 基变量系数 (目标函数) | 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | θ i \theta_i θi |
| 0 0 0 ( 目标函数 x 3 x_3 x3 系数 c 3 c_3 c3 ) | x 3 x_3 x3 | 40 40 40 | 2 2 2 | 1 1 1 | 1 1 1 | 0 0 0 | 40 40 40 ( θ 3 \theta_3 θ3 ) |
| 0 0 0 ( 目标函数 x 4 x_4 x4 系数 c 4 c_4 c4) | x 4 x_4 x4 | 30 30 30 | 1 1 1 | 3 3 3 | 0 0 0 | 1 1 1 | 10 10 10 ( θ 4 \theta_4 θ4 ) |
| σ j \sigma_j σj | 3 3 3 ( σ 1 \sigma_1 σ1 ) | 4 4 4 ( σ 2 \sigma_2 σ2 ) | 0 0 0 | 0 0 0 | |||
| – | – | – | – | – | – | – | – |
| 0 0 0 ( 目标函数 x 3 x_3 x3 系数 c 3 c_3 c3 ) | x 3 x_3 x3 | 30 30 30 | 5 3 \dfrac{5}{3} 35 | 0 0 0 | 1 1 1 | − 1 3 -\dfrac{1}{3} −31 | 18 18 18 ( θ 3 \theta_3 θ3 ) |
| 4 4 4 ( 目标函数 x 2 x_2 x2 系数 c 2 c_2 c2) | x 2 x_2 x2 | 10 10 10 | 1 3 \dfrac{1}{3} 31 | 1 1 1 | 0 0 0 | 1 3 \dfrac{1}{3} 31 | 30 30 30 ( θ 2 \theta_2 θ2 ) |
| σ j \sigma_j σj ( 检验数 ) | 5 3 \dfrac{5}{3} 35 ( σ 1 \sigma_1 σ1 ) | 0 0 0 | 0 0 0 | − 4 3 -\dfrac{4}{3} −34 ( σ 4 \sigma_4 σ4 ) |