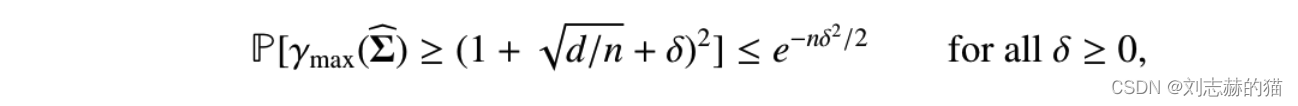随着数据量和数据特征数的增加,传统的统计方法无法满足模型和算法的分析。高维统计中的工具和方法对于分析模型和估计真值有着重要作用。
高维统计的notes主要分为两个部分:
- partA:工具和方法
- 向量:稀疏性
- 矩阵:结构性
- 无限维:结构性
- partB:一些具体的模型和估计器
这篇notes的主要内容包括:
- 高维统计的roadmap
- 高维统计和传统统计的区别
- 高维的困难(后续)
- 处理高维的工具(partA)
- 高维的实际应用
1. roadmap
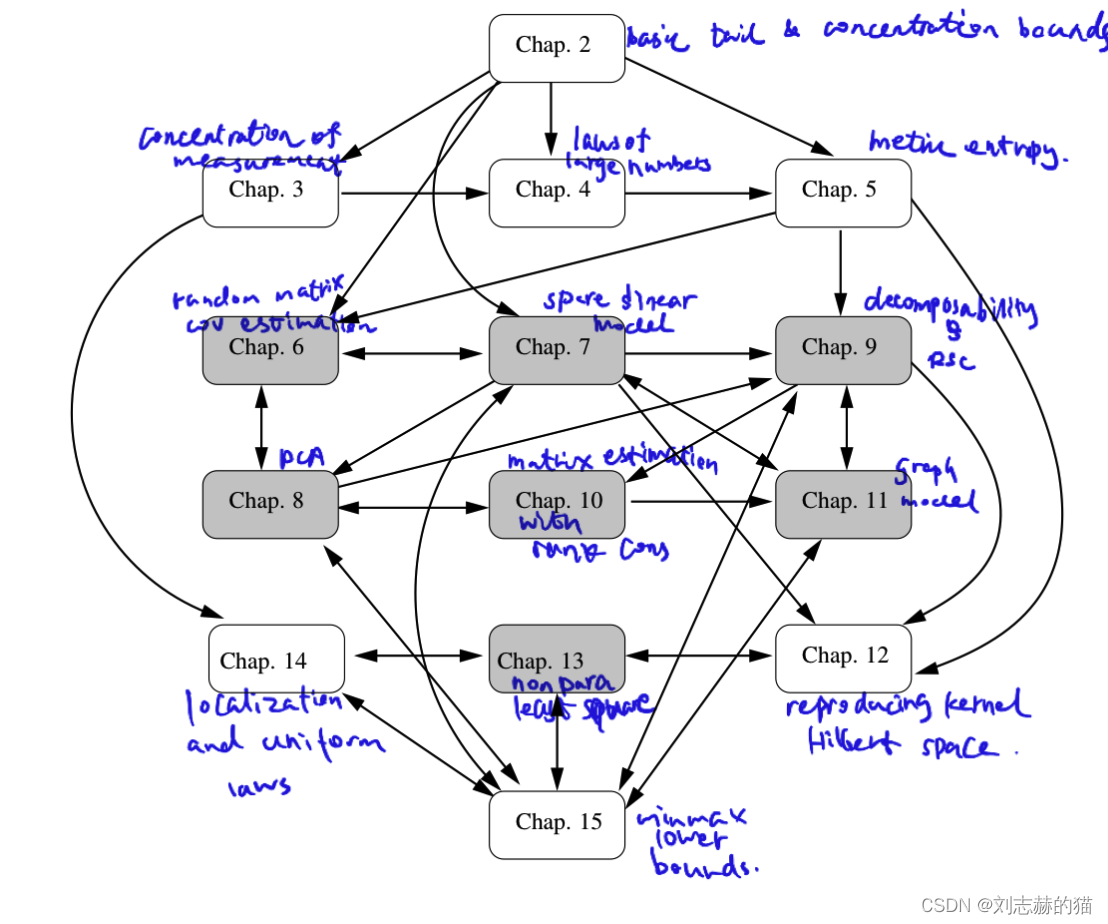
partA部分是学习高维统计用到的基本工具和方法,比如基本不等式、concentration of measurement、大数定律、metric entropy
partB部分是具体的模型和估计器,比如协方差估计、稀疏模型、PCA、可分模型、带秩约束的矩阵估计、图模型、非参数模型
除此之外还有更高级的工具和方法,比如location and uniform laws、核方法、minmax lower bounds
2. 为什么要学习高维统计
研究高维的动机:
- 实际中高维数据的普遍: d < < n d<<n d<<n,特征维度 d d d大于或者远大于样本数量 n n n
- 模型分析中,“样本量 n n n大,特征维数 d d d固定”的假设不成立
- 高维时,传统方法经常失效
传统渐进理论VS高维渐进理论VS非渐进界:
- 传统渐进理论:“ n → ∞ , f i x d n\rightarrow \infty,fix\quad d n→∞,fixd ”的假设,例如大数定理、中心极限定理
- 高维渐进理论:“ ( n , d ) → ∞ , Φ ( n , d ) f i x o r Φ ( n , d ) → α ∈ [ 0 , ∞ ) (n,d)\rightarrow \infty,\Phi(n,d) \quad fix\quad or \quad \Phi(n,d)\rightarrow \alpha\in [0,\infty) (n,d)→∞,Φ(n,d)fixorΦ(n,d)→α∈[0,∞)”的假设
- 非渐进理论:“ ( n , d ) f i x e d (n,d)\quad fixed (n,d)fixed”的假设,结论是关于其的高概率陈述
3. 一些高维统计的应用
高维统计对向量到矩阵再到无限维模型的分析都有重要应用。
3.1 线性判别分析
考虑如下二分类问题
x ∈ R d x\in R^d x∈Rd是从两个可能的分布 P 1 , P 2 \mathbb{P}_1,\mathbb{P}_2 P1,P2中抽样得到,若这两个分布已知,则根据对数似然率(log-likelihood ratio) l o g P 2 ( x ) P 1 ( x ) log \frac{\mathbb{P}_2 (x)}{\mathbb{P}_1(x)} logP1(x)P2(x)进行推断
若 P 1 , P 2 \mathbb{P}_1,\mathbb{P}_2 P1,P2为高斯分布 N ( μ 1 , Σ ) , N ( μ 2 , Σ ) N(\mu_1,\Sigma),N(\mu_2,\Sigma) N(μ1,Σ),N(μ2,Σ),此时对数似然率有:
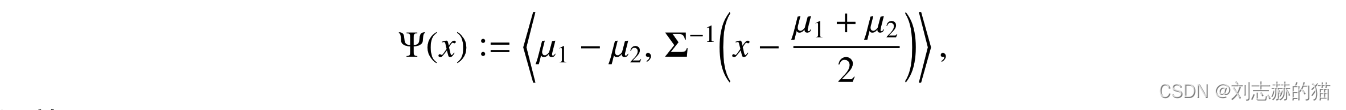
误差:
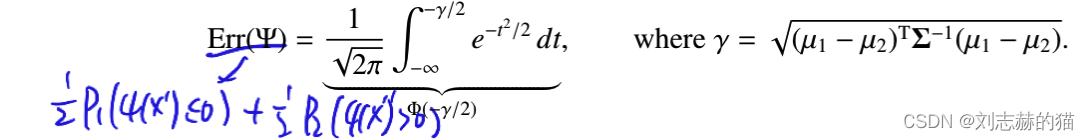
-
传统统计角度,即 d d d固定,样本量趋于无穷,由大数定律可知,以下估计量是误差的无偏估计
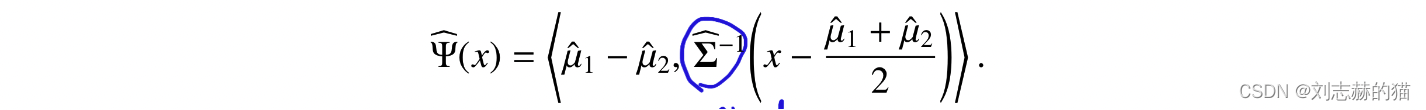
-
从高维渐进的角度,即 ( n 1 , n 2 , d ) → ∞ (n_1,n_2,d)\rightarrow \infty (n1,n2,d)→∞, d / n i → α > 0 d/n_i\rightarrow \alpha>0 d/ni→α>0
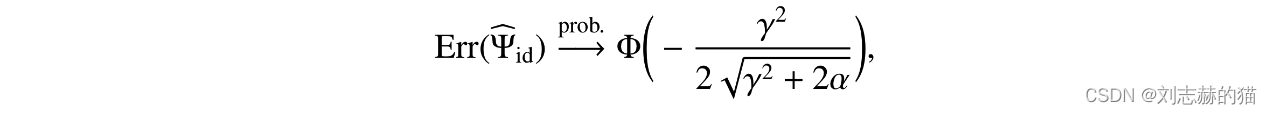
3.2 方差估计
考虑如下方差估计问题
假设随机向量集合 { x 1 , . . . , x n } \{x_1,...,x_n\} {x1,...,xn},每个随机向量 x i x_i xi服从均值 μ = 0 \mu=0 μ=0,方差 Σ \Sigma Σ的iid分布,样本均差矩阵:
- 传统统计角度,即 d d d固定,样本量趋于无穷
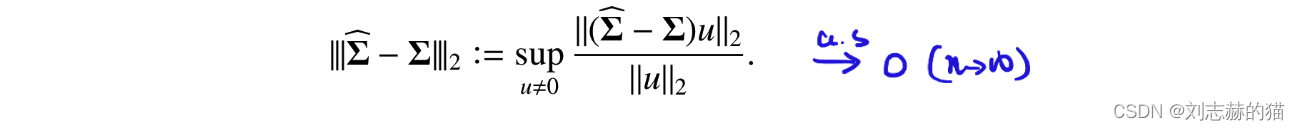
- 从高维渐进的角度,即 ( n 1 , n 2 , d ) → ∞ (n_1,n_2,d)\rightarrow \infty (n1,n2,d)→∞, d / n i → α > 0 d/n_i\rightarrow \alpha>0 d/ni→α>0