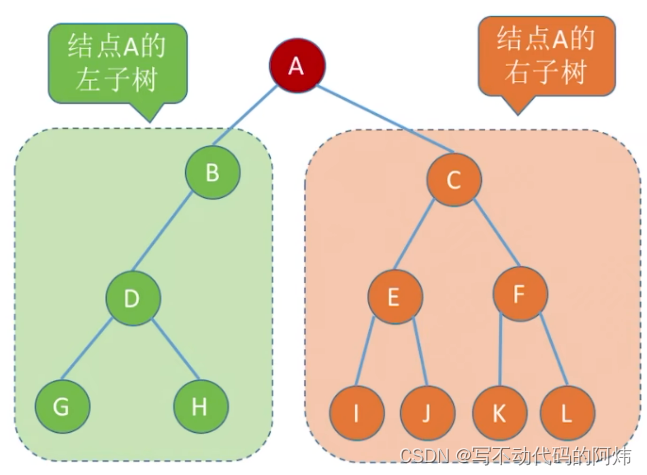
二叉树是一种特殊的树形数据结构,它对每个节点的子节点数进行了限制,即每个节点最多有两个子节点。这种结构使得二叉树成为了许多算法和数据结构的基础,如二叉搜索树、堆、哈夫曼编码等。本文将详细探讨二叉树的定义、基本术语和性质,并提供C语言实现的相关代码示例。
一.二叉树的定义
二叉树是n (n≥0)个结点的有限集合:
1或者为空二叉树,即n = 0。
2.或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
特点:①每个结点至多只有两棵子树②左右子树不能颠倒(二叉树是有序树)
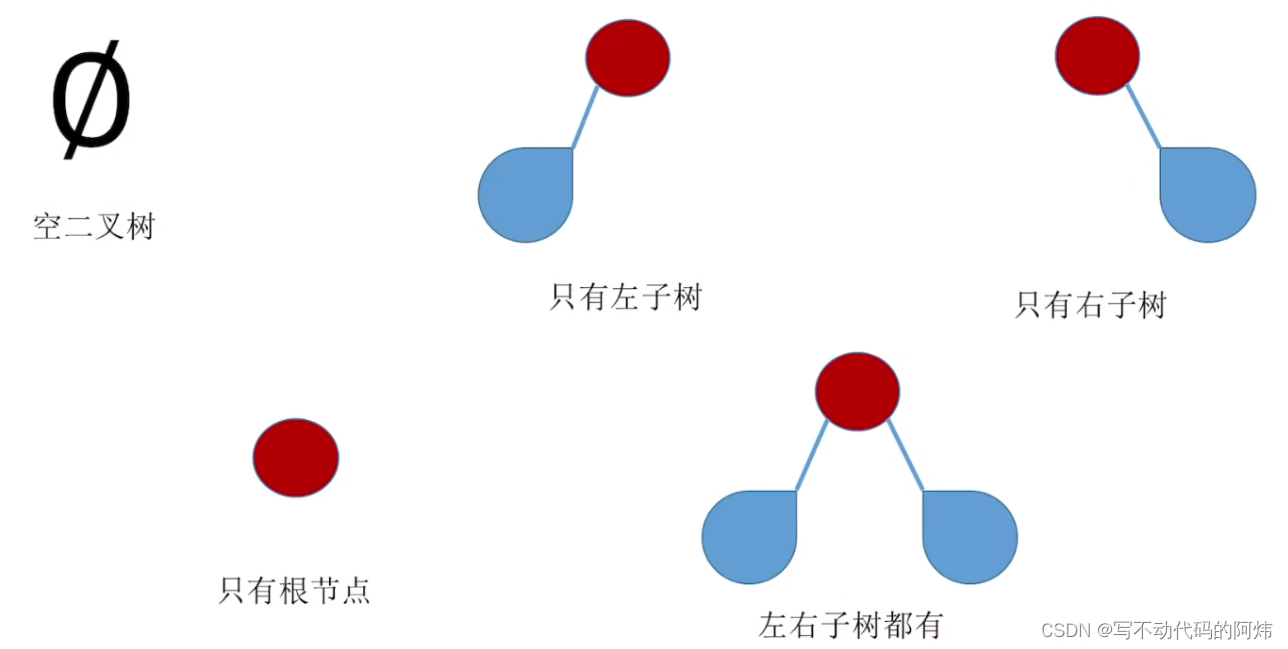
二叉树的五种状态:
二. 基本术语
1.节点:二叉树中的一个元素,包含值和指向子节点的引用(s)。
2.根:二叉树的顶部节点,没有父节点。
3.叶子:没有子节点的节点。
4.内部节点:至少有一个子节点的节点。
5.左子树/右子树:分别位于一个节点的左边和右边的子树。
6.兄弟节点:具有同一个父节点的两个节点。
7.深度:从根节点到该节点的唯一路径上的边数。
8.高度:从该节点到叶子节点的最长路径上的边数。
9.度:一个节点的子节点数(在二叉树中,度可以是0、1或2)。
三. 二叉树的性质
1. 节点数与边数的关系:在任何二叉树中,边的数量总是等于节点数减去一。
2. 唯一路径:任意两个节点之间有且仅有一条简单路径。
3. 无环:二叉树中不存在环路。
4. 完全性:所有层的节点都是满的,除了最底层,从左到右填充。
5. 平衡性:左右子树的高度差不超过1。
四.几种特殊的二叉树:
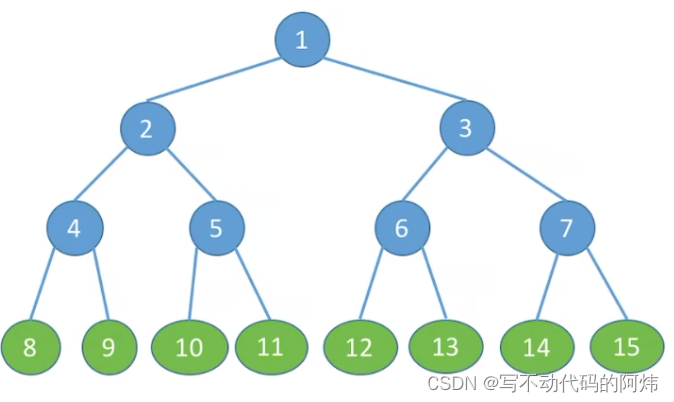
1.满二叉树:
一棵高度为h,且含有2h-1个结点的二叉树
特点:
①只有最后一层有叶子结点
②不存在度为1的结点
③按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1;结点i的父节点为Li/2](如果有的话)
2.完全二叉树:
完全二叉树。当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。
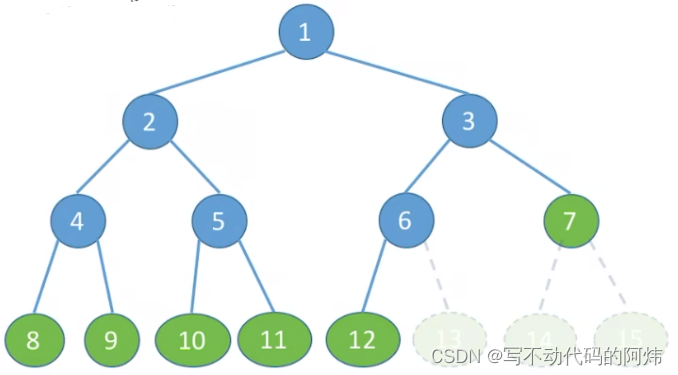
特点:
①只有最后两层可能有叶子结点
②最多只有一个度为1的结点
③同满二叉树③
④4i≤ [n/2]为分支结点,i>[n/2]为叶子结点
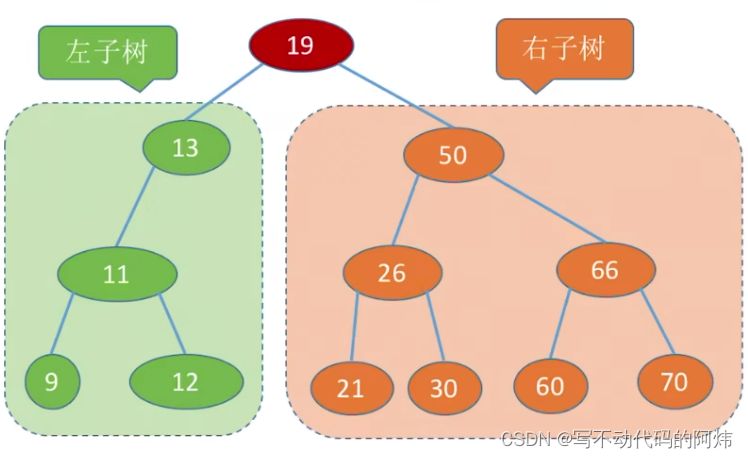
3.二叉排序树:
二叉排序树。一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
左子树上所有结点的关键字均小于根结点的关键字;
右子树上所有结点的关键字均大于根结点的关键字。
左子树和右子树又各是一棵二叉排序树。
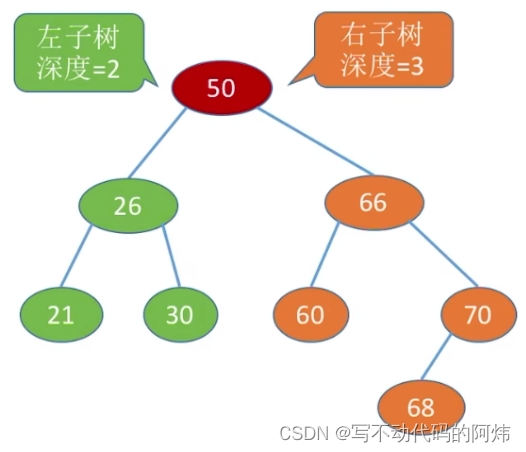
4.平衡二叉树:
树上任一结点的左子树和右子树的深度之差不超过1。
5.代码实现
#include <stdio.h>
#include <stdlib.h>// 定义二叉树节点的结构体
typedef struct Node {int data; // 节点存储的数据struct Node* left; // 左子节点指针struct Node* right; // 右子节点指针
} Node;// 创建新节点的函数
Node* createNode(int data) {Node* newNode = (Node*)malloc(sizeof(Node));if (!newNode) {printf("Memory error
");return NULL;}newNode->data = data;newNode->left = newNode->right = NULL;return newNode;
}// 插入新节点的函数
Node* insert(Node* root, int data) {if (root == NULL) {root = createNode(data);} else if (data < root->data) { // 小于当前节点值,插入左子树root->left = insert(root->left, data);} else { // 大于当前节点值,插入右子树root->right = insert(root->right, data);}return root;
}// 中序遍历打印二叉树
void inorderTraversal(Node* root) {if (root != NULL) {inorderTraversal(root->left); // 遍历左子树printf("%d ", root->data); // 访问当前节点inorderTraversal(root->right); // 遍历右子树}
}int main() {Node* root = NULL; // 初始化一个空的二叉搜索树root = insert(root, 8); // 插入根节点root = insert(root, 3);root = insert(root, 10);// ... 继续插入其他节点inorderTraversal(root); // 中序遍历并打印二叉搜索树return 0;
}以上代码实现了一个简单的二叉搜索树(Binary Search Tree),其中包含创建新节点、插入新节点以及中序遍历的功能。通过这个例子,我们可以看到二叉树这种数据结构如何在C语言中被具体实现,并且能够执行基本的树操作。