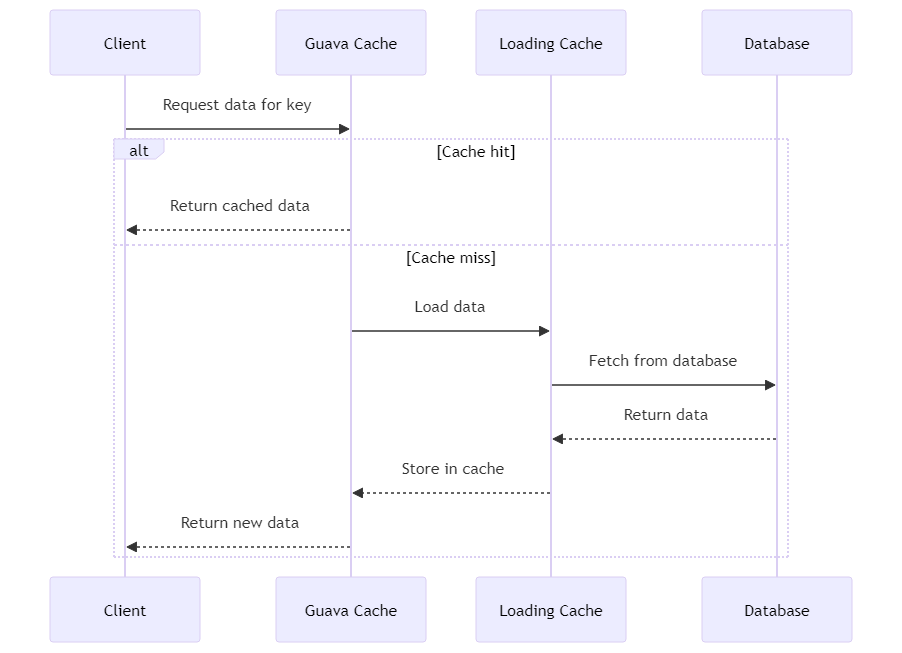
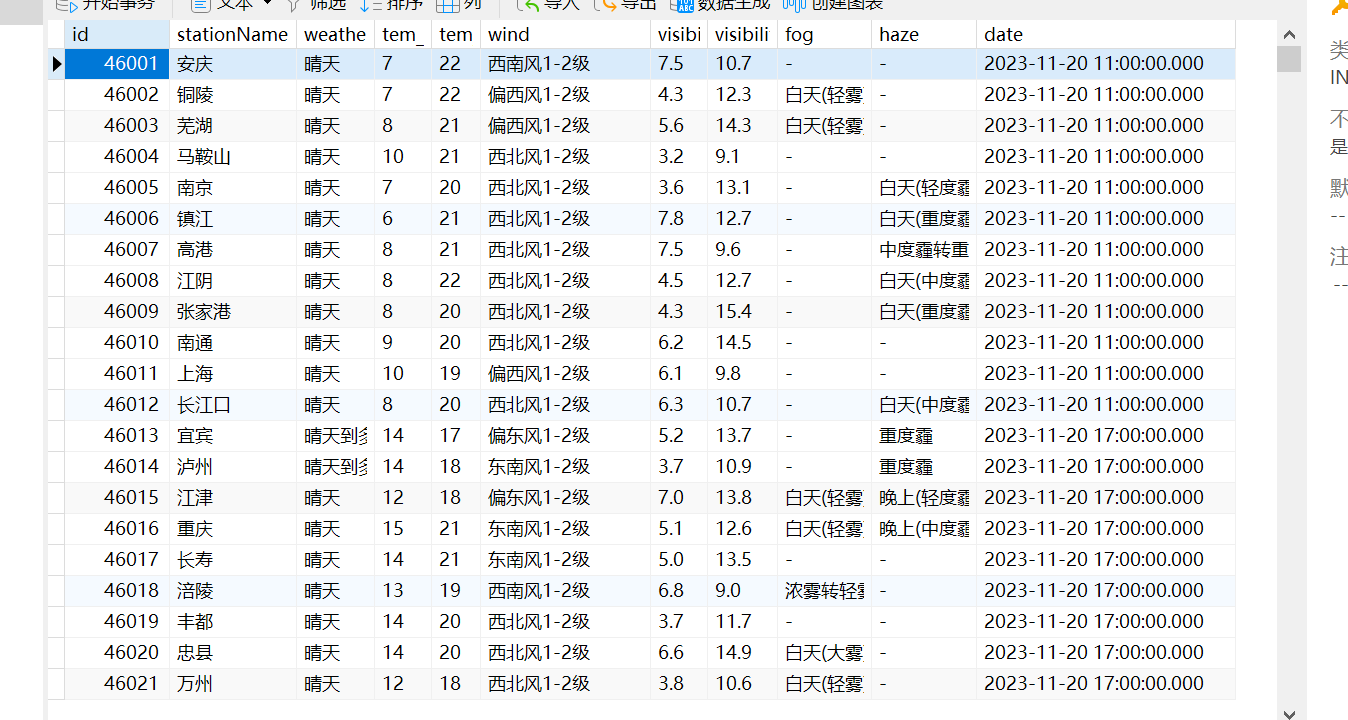
应用场景：

假设一批数据，每一个样本中，有唯一标识（id）、品类（cate_id）、受众（users, 小孩、老人、中年等）等属性，希望从其中找出一些样本，使得这些样本覆盖的品类、受众等最广。

分析：

思路是使用聚类的方式，每个簇选一个样本。观察数据，都为类别特征，常用的kmeans聚类方法，会使用欧式距离，计算两个样本之间的距离，来判断该样本是否数据该簇。对于类别特征来说，就算表示为0 ，1， 2，这些数字没有大小的意义，只代表某一个属性。所以我们不可以使用判断距离的方式，划分簇。

经过调研，认识到了两个新的聚类方法：K-modes和K-prototypes。下面分别介绍下两个方法。

K-modes

适用于离散数据，采用汉明距离

K-modes算法是按照k-means算法的核心内容进行修改，主要有以下两点：

1.度量方式。样本之间的距离D，属性相同为0，不同为1，并将所有属性结有相加。因此D越大，即他的不相关程度越强（与欧式距离代表的意义是一样的）；

汉明距离：Hamming Distance也能用来计算两个向量的相似度，通过比较向量每一位是否相同，若不同则汉明距离加1，这样得到汉明距离。向量相似度越高，对应的汉明距离越小。如10001001和10110001有3位不同。

2.更新modes，使用一个簇的每个属性出现频率最大的那个属性值作为代表簇的属性值(如｛[a,b] [a,c] [c,b] [b,c]｝)代表模式为[a,b]或者[a,c];

from kmodes.kmodes import KModesKM = KModes(n_clusters=i,init='Huang').fit_predict(X)

K-prototypes

适用于混合数据（有离散有连续）

K-Prototype算法是结合K-Means与K-modes算法，针对混合属性的，解决2个核心问题如下：

1.度量具有混合属性的方法是，数值属性采用K-means方法得到P1，分类属性采用K-modes方法P2，那么D=P1+a*P2，a是权重，如果觉得分类属性重要，则增加a，否则减少a，a=0时即只有数值属性

2.更新一个簇的中心的方法，方法是结合K-Means与K-modes的更新方法

from kmodes.kprototypes import KPrototypesKP = KPrototypes(n_clusters=self.k, init='Cao').fit_predict(X, categorical=self.dis_col)