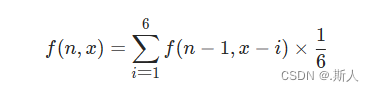跟着博主一起刷题
这里使用的是题库：
https://leetcode.cn/problem-list/xb9nqhhg/?page=1

剑指 Offer 57 - II. 和为s的连续正数序列

剑指 Offer 57 - II. 和为s的连续正数序列
这道题我的想法是利用两个指针，p1=1，p2=2，两个指针的值相加除2再乘以差值和target比较，根据大于？小于？还是等于来进行p1,p2的更新。

class Solution {public int[][] findContinuousSequence(int target) {int p1=1,p2=2;List<List<Integer>> list=new ArrayList<>();while(p2<=target/2+1){if(1.0*(p2-p1+1)*(p1+p2)/2>target){p1++;}else if(1.0*(p2-p1+1)*(p1+p2)/2<target){p2++;}else{List<Integer> line=new ArrayList<>();for(int i=p1;i<=p2;i++){line.add(i);}list.add(line);p1++;}}int[][] ret=new int[list.size()][];for(int i=0;i<list.size();i++){int[] nums=new int[list.get(i).size()];for(int j=0;j<nums.length;j++){nums[j]=list.get(i).get(j);}ret[i]=nums;}return  ret;}
}

剑指 Offer 59 - I. 滑动窗口的最大值

剑指 Offer 59 - I. 滑动窗口的最大值
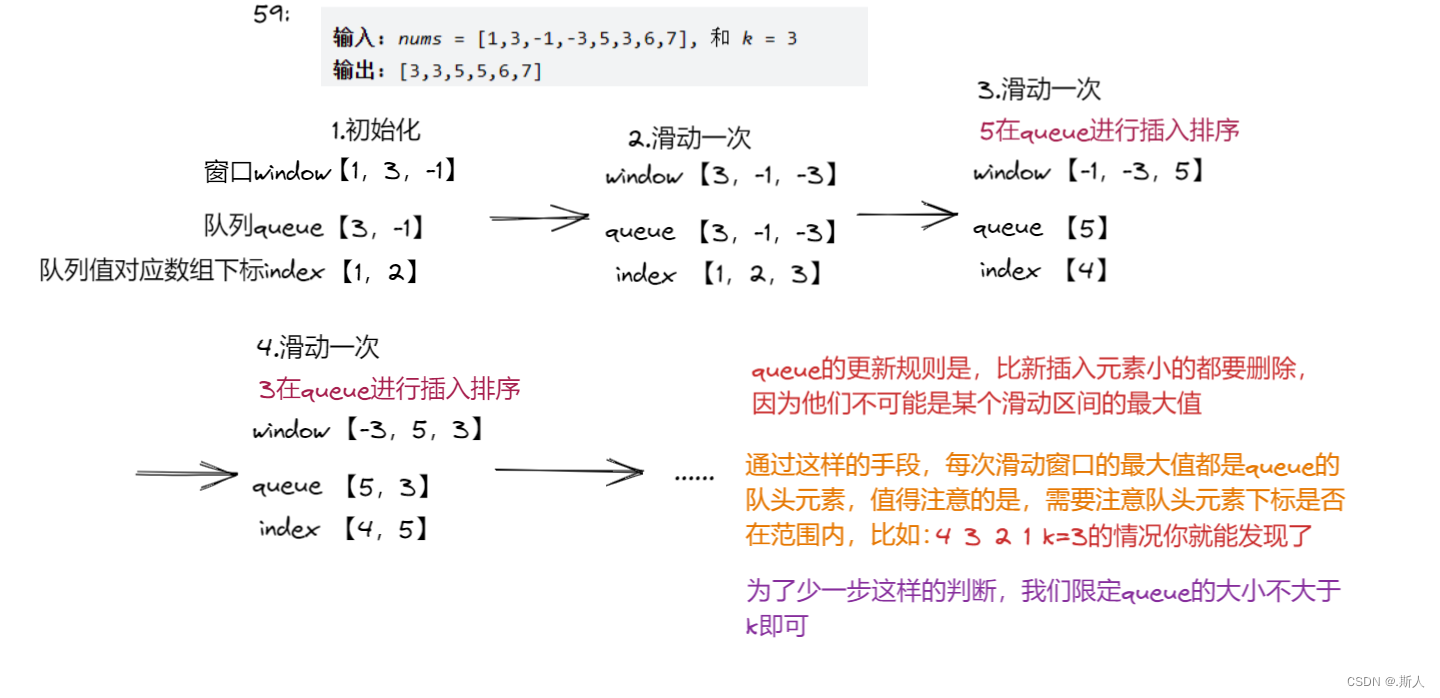
一般的思路是每滑动一次，就遍历一遍窗口内的值，找出最大。
但是这样的时间复杂度很高，是O(n*k),显然不是我们想看到的。那么怎么一次遍历就球场结果呢？
我们发现，第一种方式下，每一次求出的最大值可能再下一次滑动中还是最大值，但是我们却没有利用上，那么怎么利用上这个值呢？
我们利用一个队列queue，如图：

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {Deque<Integer> queue=new ArrayDeque<>();//记录元素Deque<Integer> index=new ArrayDeque<>();//记录下标//结果数组长度=数组长度-k+1int[] result=new int[nums.length-k+1];int left=0,right=0;int i=0;while(right<=nums.length){if(right>=k){//初始化窗口和队列后进入//把小于窗口左边界left的都弹出while(index.peekFirst()<left){index.pollFirst();queue.pollFirst();}result[i++]=queue.peekFirst();left++;}if(right==nums.length)break;while(!queue.isEmpty()&&nums[right]>=queue.peekLast()){//按插入排序找插入位置queue.pollLast();index.pollLast();}queue.offer(nums[right]);index.offer(right);right++;}return result;}
}

那么看了官方题解后，发现我们的记录数组元素queue多余的，我们只需要一个记录数组下标的queue进行了，可以剩一部分空间。
不过，这种思想的时间复杂度就缩短到了O(N)
改进后：

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {Deque<Integer> index=new ArrayDeque<>();//记录下标//结果数组长度=数组长度-k+1int[] result=new int[nums.length-k+1];int left=0,right=0;int i=0;while(right<=nums.length){if(right>=k){//初始化窗口和队列后进入//把小于窗口左边界left的都弹出while(index.peekFirst()<left){index.pollFirst();}result[i++]=nums[index.peekFirst()];left++;}if(right==nums.length)break;while(!index.isEmpty()&&nums[right]>=nums[index.peekLast()]){//按插入排序找插入位置index.pollLast();}index.offer(right);right++;}return result;}
}

只保留index即可

剑指 Offer 60. n个骰子的点数

剑指 Offer 60. n个骰子的点数
我一开始采用暴力求解的方法，即判断每一个筛子投的大小，记录结果。但是这样的时间复杂度太高了，当n==11时，发生来了时间超限。代码如下：

class Solution {  private List<Integer> list; private Map<Integer,Integer> map;private int total=0;public double[] dicesProbability(int n) {list=new ArrayList<>();map=new HashMap<>();rank(n,0);double[]  result=new double[list.size()];//对list进行排序Collections.sort(list);for(int i=0;i<result.length;i++){result[i]=1.0*map.get(list.get(i))/total;}return result;}private void rank(int n,int val){if(n==0){//抛完了total+=1;if(map.containsKey(val)){map.put(val,map.get(val)+1);}else{map.put(val,1);list.add(val);}return;}//抛出1rank(n-1,val+1);//抛出2rank(n-1,val+2);//抛出3rank(n-1,val+3);//抛出4rank(n-1,val+4);//抛出5rank(n-1,val+5);//抛出6rank(n-1,val+6);}
}

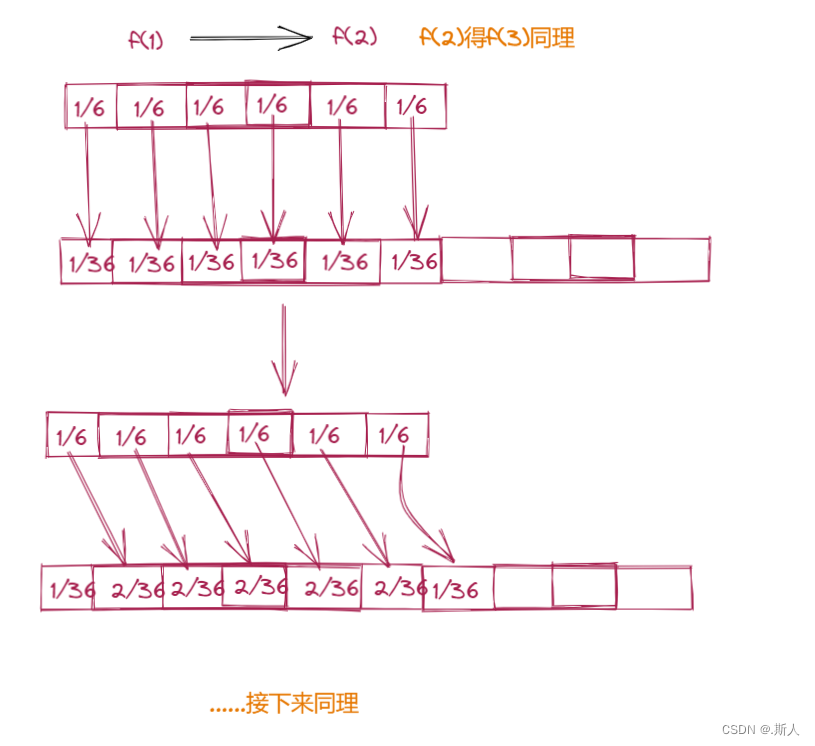
观察发现，抛出n个筛子得到的某个和x，从一定程度上取决余n-1个筛子的结果。也就是：
f(n，x)=f(n-1,x-1)(1/6)+f(n-1,x-2)(1/6)+…+f(n-1,x-6)*(1/6);
这样就得到了递推公式：

把这个递推公式反过来，我们就可以通过f(1)开始计算f(2)，一直计算到f(n)为止，也就是：

public double[] dicesProbability(int n) {double[] result=new double[6];Arrays.fill(result,1.0/6);for(int i=2;i<=n;i++){double[] tmp=new double[5*i+1];for(int j=0;j<result.length;j++){for(int k=0;k<6;k++){tmp[k+j]+=result[j]*(1.0/6);}}result=tmp;//两个数组交替使用}return result;}