数楼梯

题目描述

楼梯有 $N$ 阶，上楼可以一步上一阶，也可以一步上二阶。

编一个程序，计算共有多少种不同的走法。

输入格式

一个数字，楼梯数。

输出格式

输出走的方式总数。

样例 #1

样例输入 #1

4

样例输出 #1

5

提示

• 对于 $60\%$ 的数据，$N\le 50$；
• 对于 $100\%$ 的数据，$1\le N\le 5000$。

#include <iostream>
#include <string>
#include <cstdlib>
#include <cstring>using namespace std;#define maxn 1700struct Bigint {int len, a[maxn];Bigint(int x = 0) {memset(a, 0, sizeof(a));for (len = 1; x; len++)static_cast<void>(a[len] = x % 10), x /= 10;len--;}int& operator[](int i) {return a[i];}void flatten(int L) {len = L;for (int i = 1; i <= len; i++) {a[i + 1] += a[i] / 10;a[i] %= 10;}for (;  !a[len];) len--;}void print() {for (int i = max(len, 1); i >= 1; i--)printf("%d", a[i]);}
};Bigint operator+(Bigint a, Bigint b) {Bigint c;int len = max(a.len, b.len);for (int i = 1; i <= len; i++)c[i] += a[i] + b[i];c.flatten(len + 1);return c;
}int main() {int N;cin >> N;Bigint f[5010];f[1] = Bigint(1);f[2] = Bigint(2);for (int i = 3; i <= N; i++)f[i] = f[i - 2] + f[i - 1];f[N].print();return 0;
}

[NOIP2002 普及组] 过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0,0)$、$B$ 点 $(n,m)$，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于 $100\%$ 的数据，$1\le n,m\le 20$，$0\le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

#include <iostream>
#define NAXN 22
using namespace std;int ctrl[NAXN][NAXN];
int n, m, hx, hy;
long long f[NAXN][NAXN] = {0};
int dx[9][2] = {{0,0},{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};
//马的控制范围相对于马位置的偏移int main(){cin >> n >> m >> hx >> hy;for (int i = 0; i < 9; i++){int tmpx = hx + dx[i][0];int tmpy = hy + dx[i][1];//判断在棋盘范围内if (tmpx >= 0 && tmpx <= n && tmpy >= 0 && tmpy <= m){ctrl[tmpx][tmpy]=1;//记录马的控制点}}f[0][0] = 1 - ctrl[0][0];  //若原点就是马控制点，则初始路径数量就是0，否则是1for (int i = 0; i <= n; i++){for (int j = 0; j <= m; j++){if(ctrl[i][j]) continue;//若这个点是控制点，则跳过if (i != 0) f[i][j] += f[i - 1][j]; //若不在横轴上，上面路径数加上if (j != 0) f[i][j] += f[i][j - 1]; //若不在纵轴上，左边路径数加上}}cout << f[n][m];//输出答案return 0;
}

[NOIP2003 普及组] 栈

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

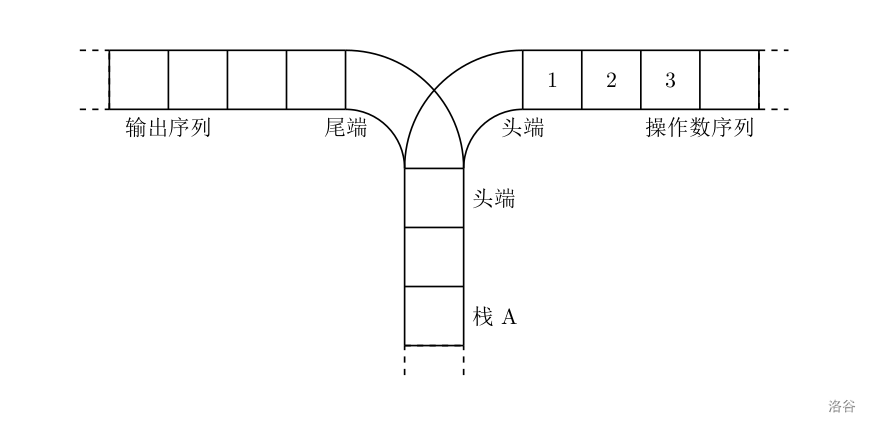
宁宁考虑的是这样一个问题：一个操作数序列，$1,2,\dots ,n$（图示为 1 到 3 的情况），栈 A 的深度大于 $n$。

现在可以进行两种操作，

1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

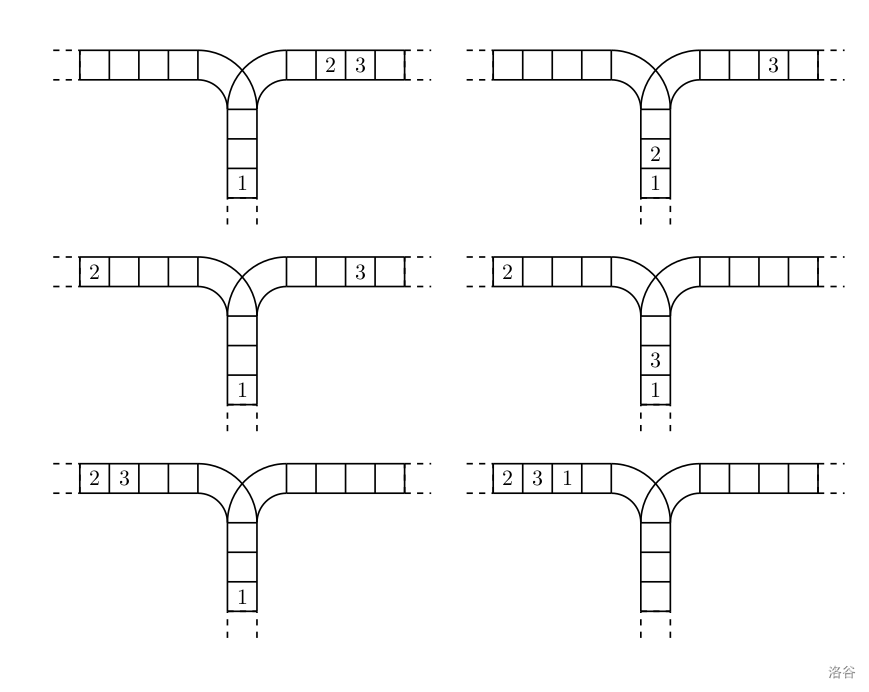
（原始状态如上图所示）

你的程序将对给定的 $n$，计算并输出由操作数序列 $1,2,\dots ,n$ 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 $n$（$1\le n\le 18$）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

样例 #1

样例输入 #1

3

样例输出 #1

5

提示

【题目来源】

NOIP 2003 普及组第三题

#include<cstdio>using namespace std;int main(){int n,h[20]={1,1};scanf("%d",&n);for(int i=2;i<=n;i++)for(int j=0;j<i;j++)h[i] += h[j]*h[i-j-1];printf("%d",h[n]);return 0;
}

[NOIP2001 普及组] 数的计算

题目描述

给出正整数 $n$，要求按如下方式构造数列：

1. 只有一个数字 $n$ 的数列是一个合法的数列。
2. 在一个合法的数列的末尾加入一个正整数，但是这个正整数不能超过该数列最后一项的一半，可以得到一个新的合法数列。

请你求出，一共有多少个合法的数列。两个合法数列 $a,b$ 不同当且仅当两数列长度不同或存在一个正整数 $i\le |a|$，使得 $a_i\ne b_i$。

输入格式

输入只有一行一个整数，表示 $n$。

输出格式

输出一行一个整数，表示合法的数列个数。

样例 #1

样例输入 #1

6

样例输出 #1

6

提示

样例 1 解释

满足条件的数列为：

• $6$
• $6,1$
• $6,2$
• $6,3$
• $6,2,1$
• $6,3,1$

数据规模与约定

对于全部的测试点，保证 $1\le n\le 10^3$。

说明

本题数据来源是 NOIP 2001 普及组第一题，但是原题的题面描述和数据不符，故对题面进行了修改，使之符合数据。原题面如下，谨供参考：

我们要求找出具有下列性质数的个数（包含输入的正整数 $n$）。

先输入一个正整数 $n$（$n\le 1000$），然后对此正整数按照如下方法进行处理：

1. 不作任何处理；
2. 在它的左边拼接一个正整数，但该正整数不能超过原数，或者是上一个被拼接的数的一半；
3. 加上数后，继续按此规则进行处理，直到不能再加正整数为止。

感谢 @dbxxx 对本题情况的反馈，原题面的问题见本贴。

#include<iostream>
#include<cstring>using namespace std;int n,f[1010];int sol(int x){int ans = 1;if(f[x]!=-1)return f[x];for(int i=1;i<=x/2;i++)ans+=sol(i);return f[x] = ans;
}int main(){cin>>n;memset(f,-1,sizeof(f));f[1]=1;cout<<sol(n)<<endl;return 0;
}

Function

题目描述

对于一个递归函数 $w(a,b,c)$

• 如果 $a\le 0$ 或 $b\le 0$ 或 $c\le 0$ 就返回值$ 1$。
• 如果 $a>20$ 或 $b>20$ 或 $c>20$ 就返回 $w(20,20,20)$
• 如果 $a<b$ 并且 $b<c$ 就返回$ w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c)$。
• 其它的情况就返回 $w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1)$

这是个简单的递归函数，但实现起来可能会有些问题。当 $a,b,c$ 均为 $15$ 时，调用的次数将非常的多。你要想个办法才行。

注意：例如 $w(30,-1,0)$ 又满足条件 $1$ 又满足条件 $2$，请按照最上面的条件来算，答案为 $1$。

输入格式

会有若干行。

并以 $-1,-1,-1$ 结束。

输出格式

输出若干行，每一行格式：

w(a, b, c) = ans

注意空格。

样例 #1

样例输入 #1

1 1 1
2 2 2
-1 -1 -1

样例输出 #1

w(1, 1, 1) = 2
w(2, 2, 2) = 4

提示

数据规模与约定

保证输入的数在 $[-9223372036854775808,9223372036854775807]$ 之间，并且是整数。

保证不包括 $-1,-1,-1$ 的输入行数 $T$ 满足 $1\le T\le 10^5$。

#include <iostream>
using namespace std;long long f[25][25][25];long long w(long long a, long long b, long long c) {if (a <= 0 || b <= 0 || c <= 0) return 1;else if (a > 20 || b > 20 || c > 20) return w(20, 20, 20);else if (f[a][b][c]!=0)return f[a][b][c];else if (a == b && b < c)f[a][b][c] = w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);elsef[a][b][c] = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1);return f[a][b][c];
}int main() {long long a, b, c;while (cin >> a >> b >> c) {if (a == -1 && b == -1 && c == -1)break;cout << "w(" << a << ", " << b << ", " << c << ") = ";cout << w(a, b, c) << endl;}return 0;
}

外星密码

题目描述

有了防护伞，并不能完全避免 2012 的灾难。地球防卫小队决定去求助外星种族的帮助。经过很长时间的努力，小队终于收到了外星生命的回信。但是外星人发过来的却是一串密码。只有解开密码，才能知道外星人给的准确回复。解开密码的第一道工序就是解压缩密码，外星人对于连续的若干个相同的子串 $\text{X}$ 会压缩为 $\text{[DX]}$ 的形式（$D$ 是一个整数且 $1\le D\le 99$），比如说字符串 $\text{CBCBCBCB}$ 就压缩为 $\text{[4CB]}$ 或者$\text{[2[2CB]]}$，类似于后面这种压缩之后再压缩的称为二重压缩。如果是 $\text{[2[2[2CB]]]}$ 则是三重的。现在我们给你外星人发送的密码，请你对其进行解压缩。

输入格式

输入一行，一个字符串，表示外星人发送的密码。

输出格式

输出一行，一个字符串，表示解压缩后的结果。

样例 #1

样例输入 #1

AC[3FUN]

样例输出 #1

ACFUNFUNFUN

提示

【数据范围】

对于 $50\%$ 的数据：解压后的字符串长度在 $1000$ 以内，最多只有三重压缩。

对于 $100\%$ 的数据：解压后的字符串长度在 $20000$ 以内，最多只有十重压缩。保证只包含数字、大写字母、[ 和 ]。

#include <iostream>
#include <cstring>
using namespace std;string expand() {string s = "",X;char c;int D;while (cin >> c) { // 持续读入字符，直到全部读完if (c == '[') { // 发现一个压缩区cin >> D; // 读入DX = expand(); // 递归地读入Xwhile (D--)s += X; // 重复D次X并进行拼接} else if (c == ']') {return s; // 压缩区结束，返回已经处理好的s} else {s += c; // 如果不是'['和']'，那还是s的字符，加进去即可}}return s;
}int main() {cout << expand();return 0;
}