目录
1、Cp、Cpk、Pp、Ppk
2、python计算
1、Cp、Cpk、Pp、Ppk
Cp= Process Capability Ratio 可被译为“过程能力指数”
Cpk= Process Capability K Ratio 可被译为“过程能力K指数”
Pp= Process Performance Ratio 可被译为“过程绩效指数”
Ppk= Process Performance K Ratio 可被译为“过程绩效K指数”
当 Cpk<1说明制程能力差,不可接受。
1≤Cpk≤1.33,说明制程能力可以,但需改善。
1.33≤Cpk≤1.67,说明制程能力正常。
过程绩效指数(Pp和Ppk)是过程的过去或现实;而过程能力指数(Cp和Cpk)是过程的潜能或将来。过程能力指数的计算必须满足"过程稳定"和"数据正态分布"两个必要条件;而用于Pp和Ppk计算的数据则不必进行这两个测试。过程能力指数及过程绩效指数的数学关系是:Cp≥Pp , Cpk≥Ppk。当过程稳定(stable或under control)且数据呈正态分布时Cp=Pp,Cpk=Ppk(注意这里的"="是统计学意义上的相同);只要有特殊原因存在, Cp>Pp , Cpk>Ppk。理解这一点对它们的应用很关键。
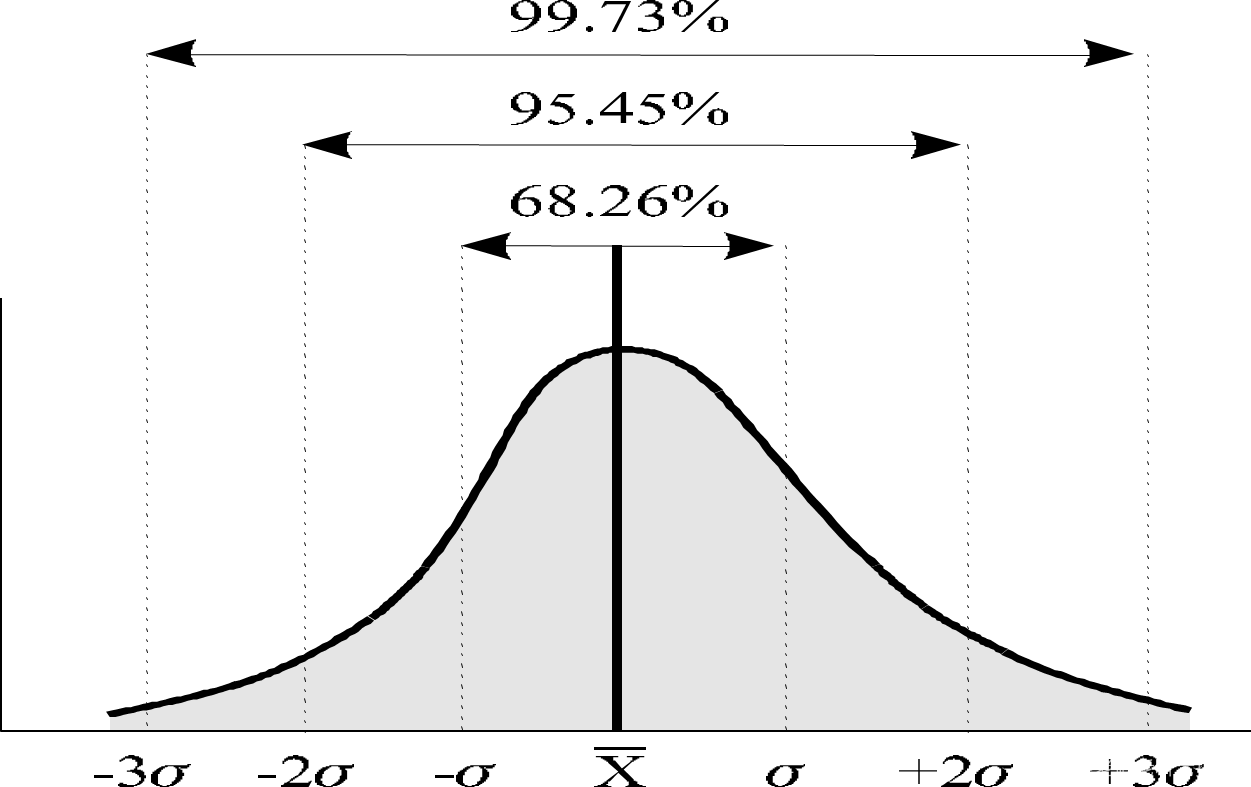
如果想知道目前的过程是否已经是达到了稳定的潜在状态时,可以比较过程能力指数和过程绩效指数的差别,即Cp和Pp, Cpk和Ppk的差别:二者差别越小,说明目前的过程的绩效越接近稳定状态,即过程不存在太多的特殊原因引起的偏离(variation)。如果差异很大,则说明过程不稳定,需要找出那些特别的原因,消除这些原因,过程即可被改进。管理者也可以利用过程能力指数和过程绩效指数的差别,制订不断改进的目标。
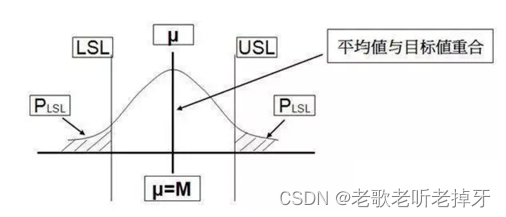

2、python计算
import numpy as np
import matplotlib.pyplot as plt
def Cp(data,USL,LSL):""":param data: 数据:param USL: 数据指标上限:param LSL: 数据指标下限:return:"""# 计算每组的平均值和标准差sigma = np.std(data, axis=1)m, n = np.shape(data)sum=0for i in range(m):sum+=(n-1)*sigma[i]**2s=np.sqrt(sum/(m*n-m))cp=(USL-LSL)/6/sreturn cp
def Cpk(data,USL,LSL):""":param data: 数据:param USL: 数据指标上限:param LSL: 数据指标下限:return:"""u = np.mean(data)sigma = np.std(data, axis=1)m, n = np.shape(data)sum = 0for i in range(m):sum += (n - 1) * sigma[i] ** 2s = np.sqrt(sum / (m * n - m))cpk=min(USL-u,u-LSL)/3/sreturn cpk
def Pp(data,USL,LSL):""":param data: 数据:param USL: 数据指标上限:param LSL: 数据指标下限:return:"""sigma=np.std(data)pp=(USL-LSL)/6/sigmareturn pp
def Ppk(data,USL,LSL):""":param data: 数据:param USL: 数据指标上限:param LSL: 数据指标下限:return:"""u=np.mean(data)sigma = np.std(data)ppk=min(USL-u,u-LSL)/3/sigmareturn ppk# 使用matplotlib画图
data=np.random.normal(0, 1, (25, 5))
cp=Cp(data,2,-2)
cpk=Cpk(data,2,-2)
pp=Pp(data,2,-2)
ppk=Ppk(data,2,-2)
print("Cp=",cp,"Cpk=",cpk,"Pp=",pp,"Ppk=",ppk)
Cp= 0.7068034057688628 Cpk= 0.705282201140378 Pp= 0.6345352278919454 Ppk= 0.6331695611199301