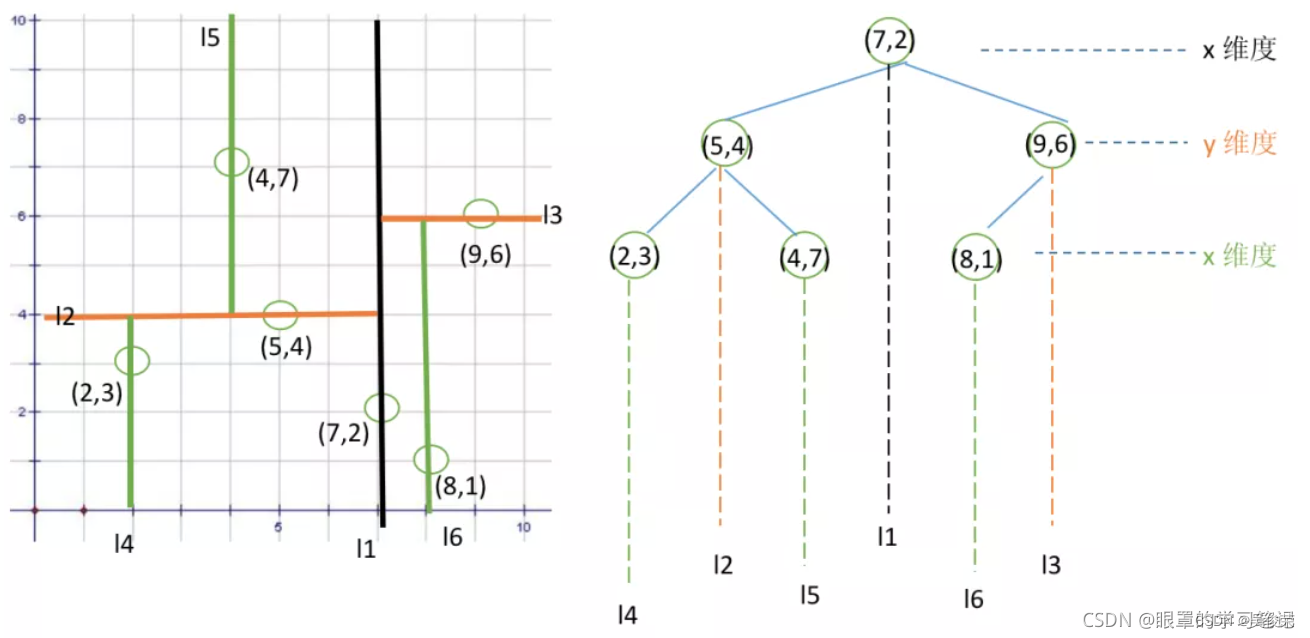
KD树（K-Dimensional Tree）是一种用于多维空间的二叉树数据结构，旨在提供高效的数据检索。KD树在空间搜索和最近邻搜索等问题中特别有用，允许在高维空间中有效地搜索数据点。
重要性质
1.分割K维数据空间的数据结构
2.是一颗二叉树
3.切分维度上，左子树值小于右子树值

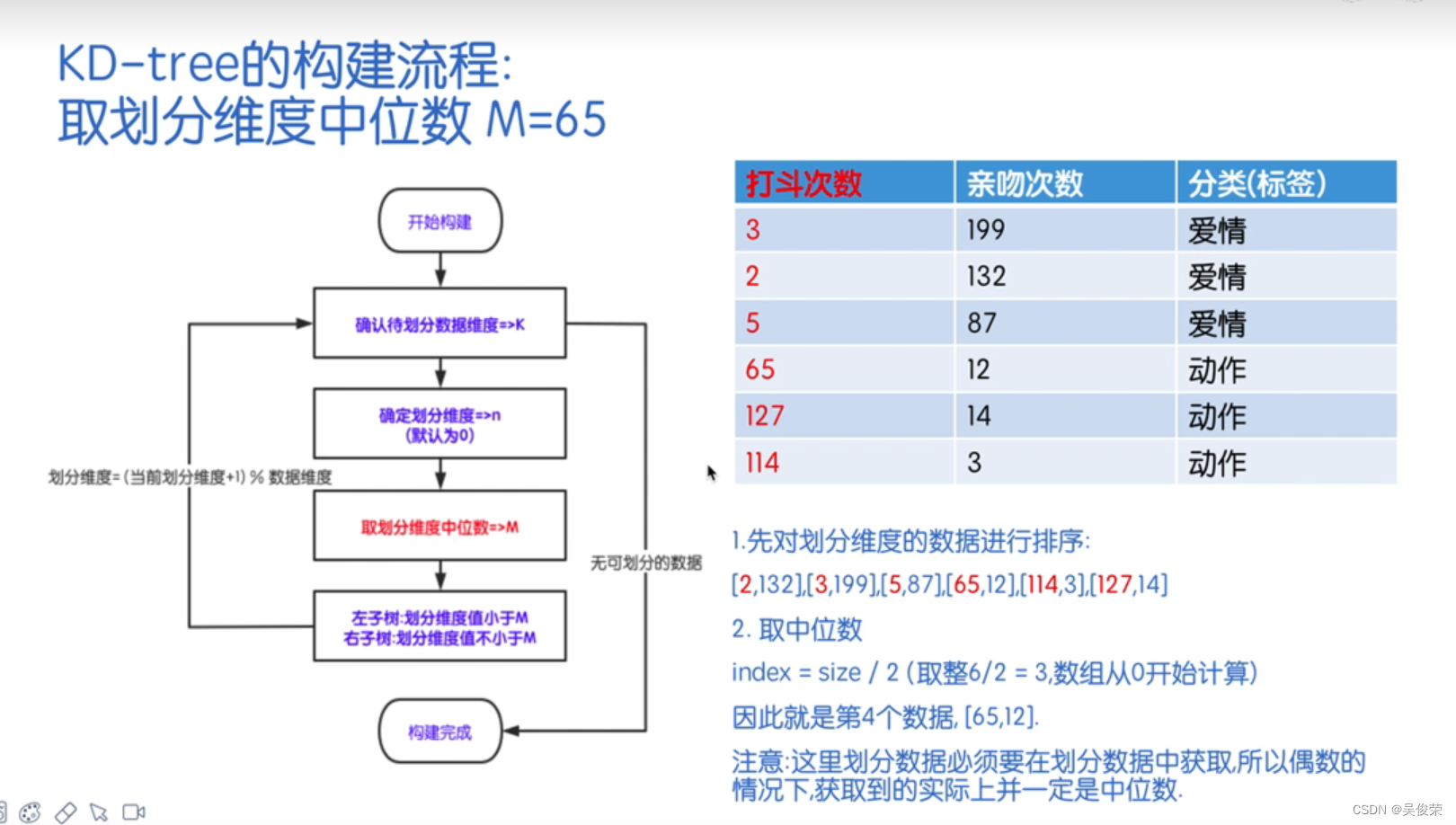
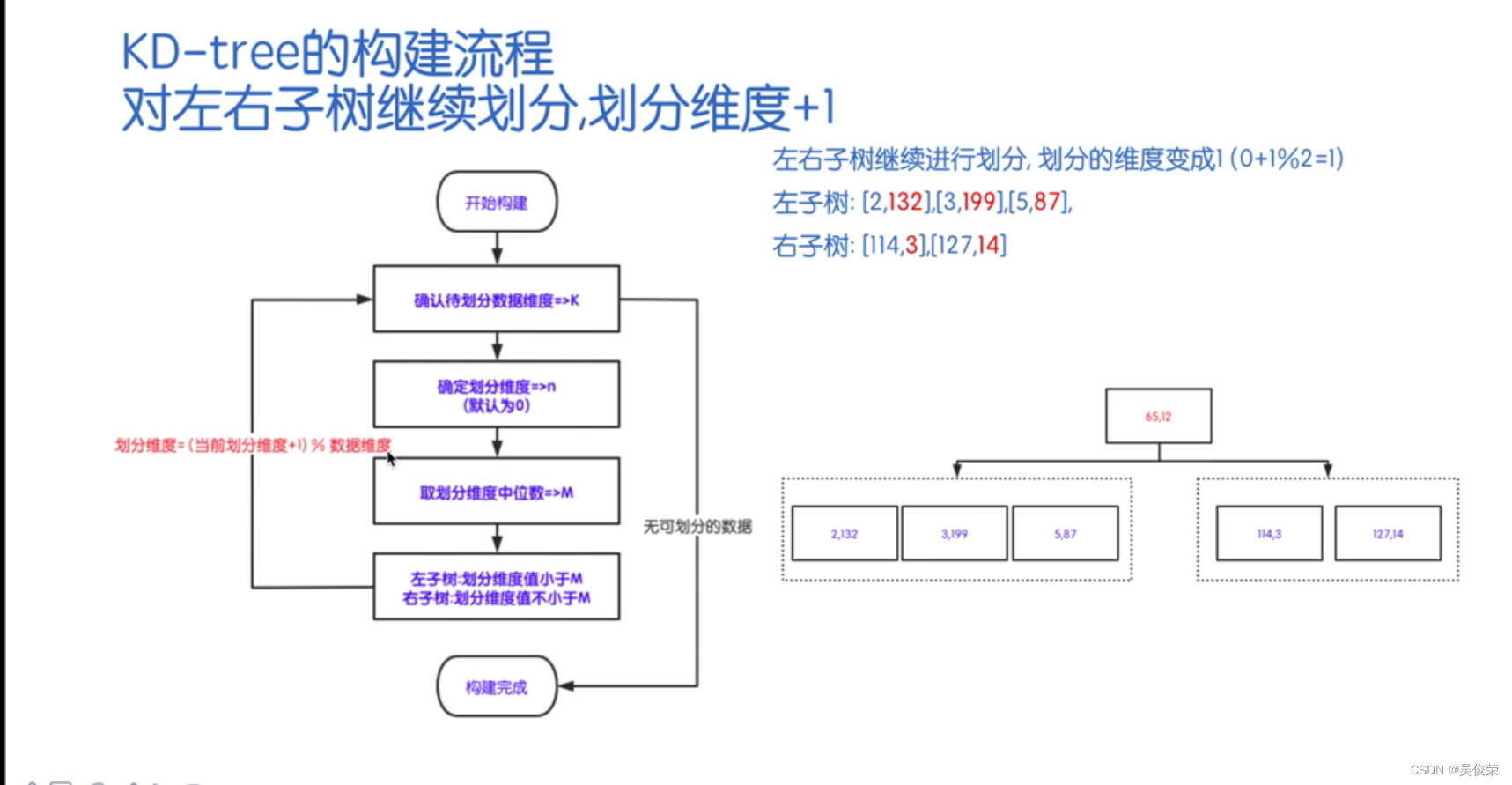
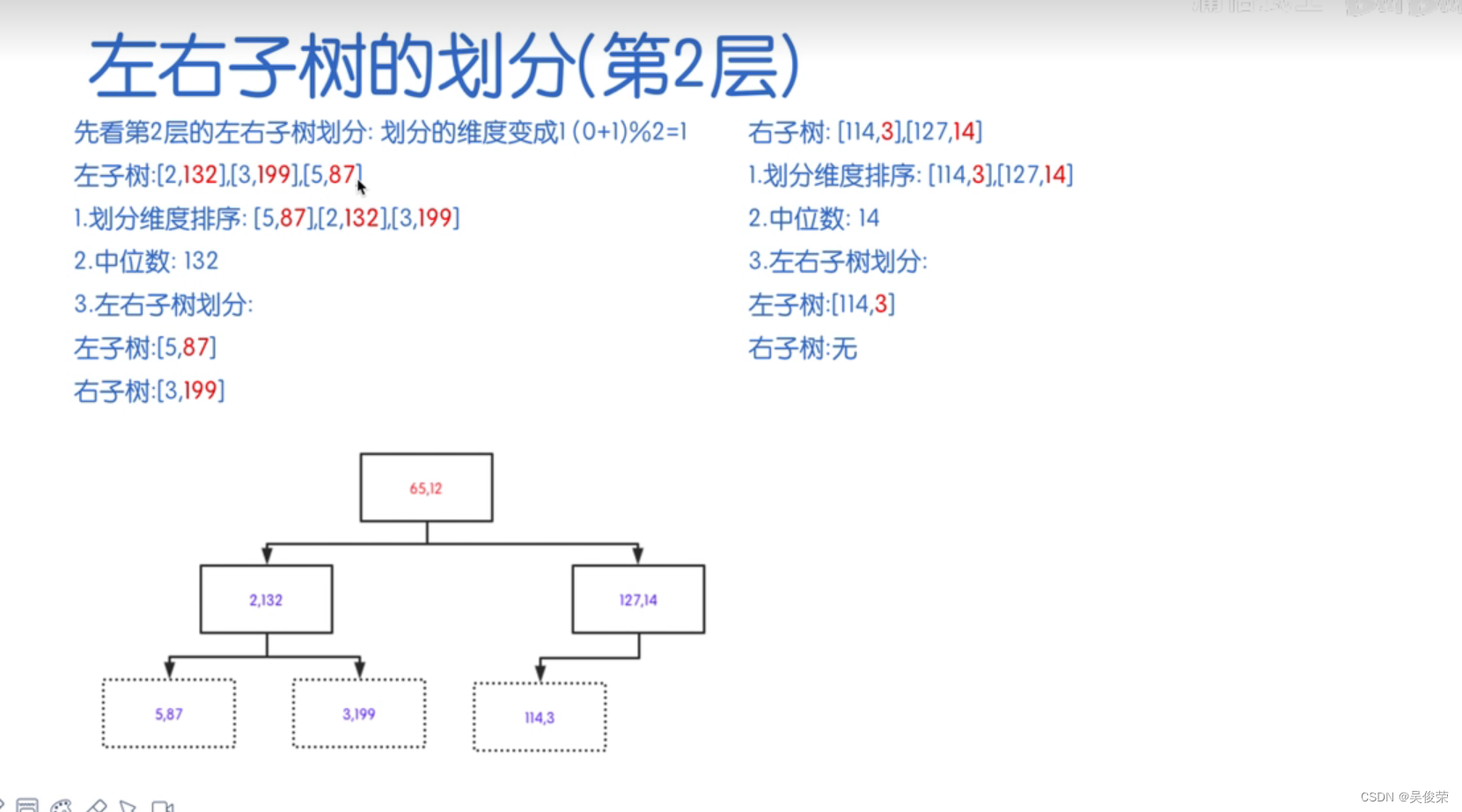
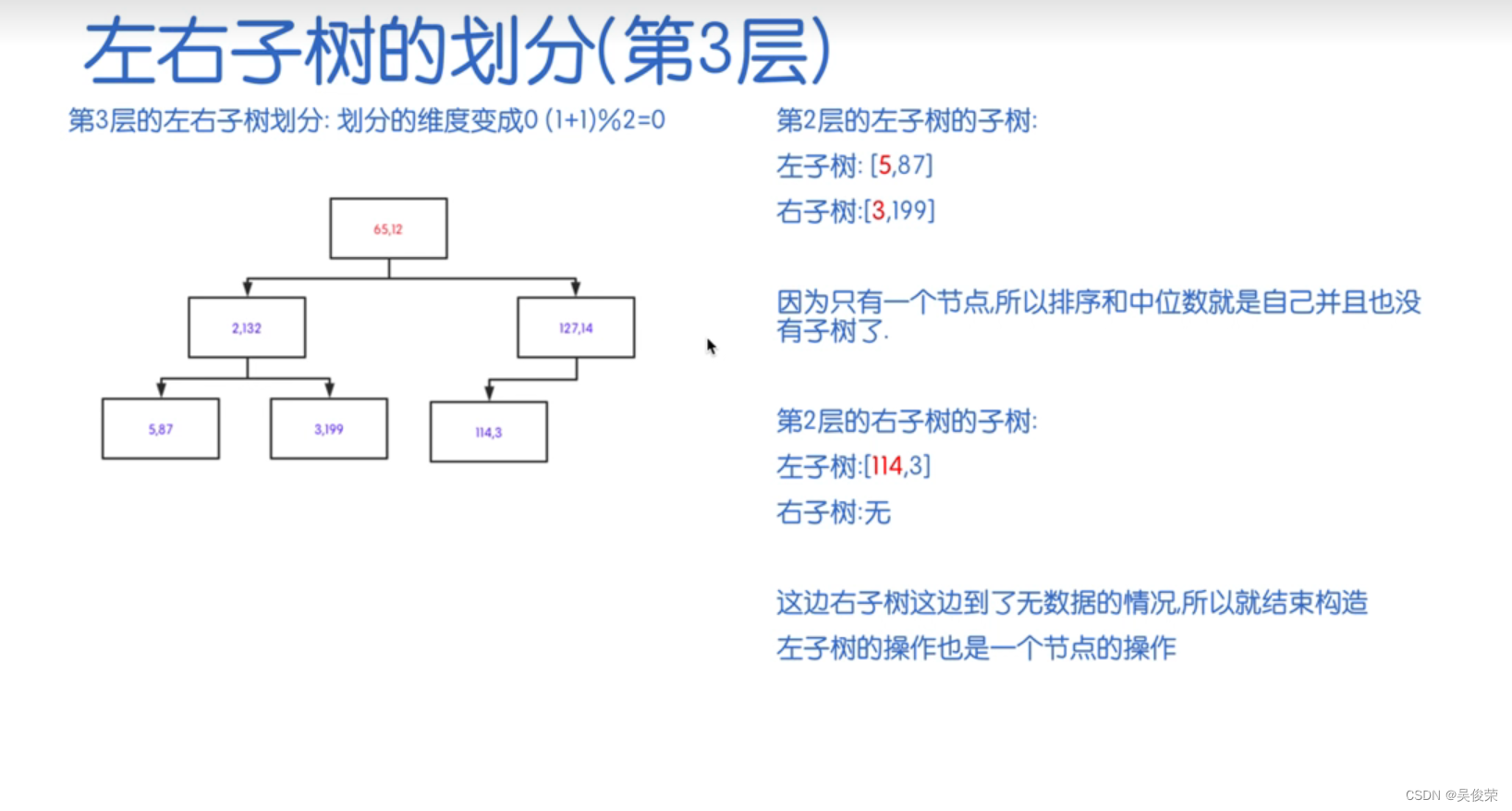
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>// 定义二维点的结构体
struct Point2D {double x;double y;Point2D(double _x, double _y) : x(_x), y(_y) {}
};// 定义KD树节点
struct KDTreeNode {Point2D point;KDTreeNode* left;KDTreeNode* right;KDTreeNode(Point2D _point) : point(_point), left(nullptr), right(nullptr) {}
};class KDTree {
private:KDTreeNode* root;// 构建KD树的递归函数KDTreeNode* buildKDTree(std::vector<Point2D>& points, int depth) {if (points.empty()) {return nullptr;}// 选择轴线，交替选择x和y坐标int axis = depth % 2;// 按轴线排序点if (axis == 0) {std::sort(points.begin(), points.end(), [](const Point2D& a, const Point2D& b) {return a.x < b.x;});} else {std::sort(points.begin(), points.end(), [](const Point2D& a, const Point2D& b) {return a.y < b.y;});}// 选择中间点作为节点int median = points.size() / 2;KDTreeNode* node = new KDTreeNode(points[median]);// 递归构建左子树和右子树std::vector<Point2D> leftPoints(points.begin(), points.begin() + median);std::vector<Point2D> rightPoints(points.begin() + median + 1, points.end());node->left = buildKDTree(leftPoints, depth + 1);node->right = buildKDTree(rightPoints, depth + 1);return node;}// 在KD树中查找最近邻点的递归函数KDTreeNode* findNearestNeighbor(KDTreeNode* node, Point2D target, int depth, KDTreeNode* best, double& bestDistance) {if (node == nullptr) {return best;}// 计算当前节点到目标点的距离double currentDistance = distance(node->point, target);// 更新最近邻点和距离if (currentDistance < bestDistance) {best = node;bestDistance = currentDistance;}// 选择子树int axis = depth % 2;KDTreeNode* nearSubtree;KDTreeNode* farSubtree;if (axis == 0) {if (target.x < node->point.x) {nearSubtree = node->left;farSubtree = node->right;} else {nearSubtree = node->right;farSubtree = node->left;}} else {if (target.y < node->point.y) {nearSubtree = node->left;farSubtree = node->right;} else {nearSubtree = node->right;farSubtree = node->left;}}// 递归搜索更近的子树best = findNearestNeighbor(nearSubtree, target, depth + 1, best, bestDistance);// 如果可能，搜索更远的子树if (shouldSearchFarSubtree(node, target, bestDistance)) {best = findNearestNeighbor(farSubtree, target, depth + 1, best, bestDistance);}return best;}// 计算两点之间的欧几里得距离double distance(Point2D a, Point2D b) {double dx = a.x - b.x;double dy = a.y - b.y;return std::sqrt(dx * dx + dy * dy);}// 检查是否需要搜索更远的子树bool shouldSearchFarSubtree(KDTreeNode* node, Point2D target, double bestDistance) {int axis = node->point.x > target.x ? 0 : 1; // 如果轴线是x，则比较x坐标；如果轴线是y，则比较y坐标double nodeDistance = axis == 0 ? node->point.x - target.x : node->point.y - target.y;return nodeDistance * nodeDistance < bestDistance;}public:KDTree(std::vector<Point2D>& points) {root = buildKDTree(points, 0);}// 查找最近邻点Point2D findNearestNeighbor(Point2D target) {double bestDistance = std::numeric_limits<double>::max();KDTreeNode* bestNode = findNearestNeighbor(root, target, 0, nullptr, bestDistance);return bestNode->point;}
};int main() {// 创建一些二维点std::vector<Point2D> points = {{2.0, 3.0},{5.0, 4.0},{9.0, 6.0},{4.0, 7.0},{8.0, 1.0},{7.0, 2.0}};// 构建KD树KDTree kdTree(points);// 查找最近邻点Point2D target(9.0, 2.0);Point2D nearestNeighbor = kdTree.findNearestNeighbor(target);std::cout << "The nearest neighbor to (" << target.x << ", " << target.y << ") is (" << nearestNeighbor.x << ", " << nearestNeighbor.y << ")" << std::endl;return 0;
}