弗洛伊德算法的适用情况：弗洛伊德算法既可以用来求解有向网的最短路径长度，也可以用来求无向网的最短路径长度，但是对于图中出现负权环的情况，弗洛伊德无法的得到正确的答案
弗洛伊德的算法思想：
以此图为例讲解弗洛伊德算法的算法步骤：
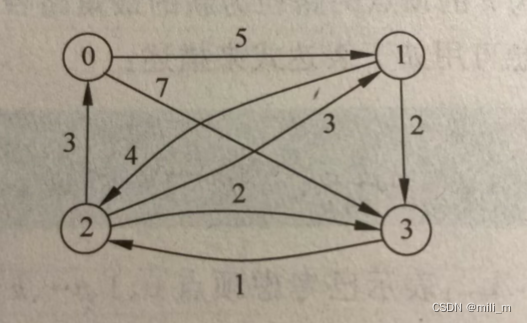
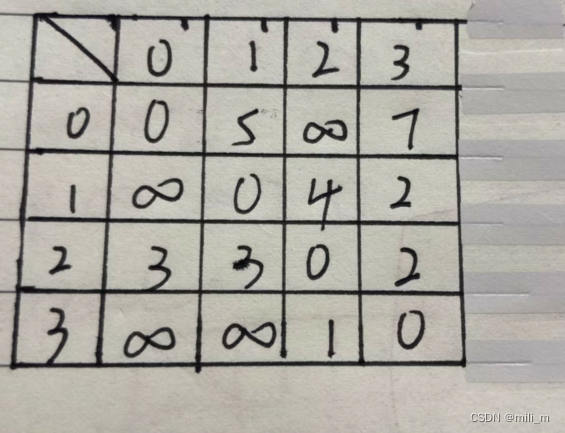
- 第一步将图用邻接矩阵的数据结构存储，得到一张二维表记作ArcInfor，顶点到其自身的边权值记为0，若两个顶点之间没有直达的边则即为无穷大，如图所示：
对于图的邻接矩阵的存储结构不了解的读者可以去看我的这篇博客：http://t.csdn.cn/aQaTI这篇博客里面讲了图的基本知识以及图的顺序存储方式（邻接矩阵）以及链式存储方式（邻接表）的实现过程，就是有点长可能需要一点耐心才可以看的下去 - 第二步，以0作为中间顶点，求每一个顶点经过顶点0到达其他顶点的路径长度，若该长度小于上表表项，则更新上表，比如以0为中间结点，求顶点2途径中间顶点0到达顶点3的路径长度为：ArcInfor[2][0[+ArcInfor[0][3]=10>ArcInfor[2][3]，因此不更新此表项
- 第三步就是重复第二步依次将其他顶点作为中间顶点，然后求每一个顶点途径此顶点到达其它顶点的路径长度，然后符合条件就更新表项，最终得到的二维表arc中就记录了任意两对顶点之间的最短路径的长度
从以上算法思想我们已经可以得到一个大致的思路就是弗洛伊德算法只需要借助简单的三重for循环就可以实现，如
void FloydAlgorithm(int v[V],int arc[V][V],int spath[V][V])
{//只需要用到三重for循环即可实现弗洛伊德算法for (int k = 0; k < V; k++){for (int i = 0; i < V; i++){for (int j = 0; j < V; j++){if (arc[i][k] + arc[k][j] < arc[i][j]){arc[i][j] = arc[i][k] + arc[k][j];spath[i][j] = k;}}}}//打印最短路径print_spath(v, arc, spath);}最外层循环控制变量是用于实现步骤“依次将每一个顶点作为中间顶点“，而内层的两层循环是用于实现”以某个顶点作为中间节点时，每一个顶点经过此结点到达其它顶点的最短路径“；
对于这题，我们不禁想要得到一个简单的最短路径长度，我们还期望得到任意两个顶点之间的最短路径，即将路径上途径的顶点输出；这里我们需要借助一个二维矩阵spath来实现，spath[i][j]的含义是，顶点i与j之间的中间顶点；输出对最短路径的代码如下，对于输出最短路径的代码，读者可能不是很清楚，这时候可以把我的代码调试一遍，观察各个变量取值的变化情况，这样你就能理解算法的设计思路了，对于我来说，我每次看不太懂别人的代码的时候用的都是此方法
//以下函数用于输出两个顶点之间的最短路径间需要经过那些顶点，不包括源节点和目的节点
void output(int v[V],int spath[V][V],int start,int end) //start，end表示的是顶点所在的数组中的下标。
{//该函数需要用到递归思想，我们从右往左输出源节点到目的节点所经过的顶点的信息int k = spath[start][end]; //即从start到end中间需要经过的一个顶点再顶点数组中的下标if (k == -1){return;}output(v, spath, start, k);printf("%d->", v[k]);output(v, spath, k, end);
}//以下函数用于打印图中任意两个结点之间的最短路径
void print_spath(int v[V],int arc[V][V],int spath[V][V])
{for (int i = 0; i < V; i++){for (int j = 0; j < V; j++){if (i == j){continue;}else{if (arc[i][j] >= INF){printf("%d->%d之间不存在路径\n", v[i], v[j]);}else{printf("%d->%d之间的最短路径长度为：%d\n", v[i],v[j],arc[i][j]);printf("%d->%d之间的最短路径为:\n", v[i], v[j]);printf("%d->", v[i]);output(v, spath, i, j);printf("%d\n", v[j]);}}}}
}完整程序源代码以及运行结果截图：
程序源代码：
//用弗洛伊德算法求图的最短路径//弗洛伊德算法既可以用来求无向图的最短路径，也可以用来求有向图的最短路径；//注意：弗洛伊德算法不可以用于求存在负权环的图的最短路径#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>#define V 4 //顶点的数目
#define INF 60000 //用于定义一个大数，当两个顶点之间不存在边或者弧时，在邻接矩阵中的对应位置上填上该大数,infinity:无穷大//采用邻接矩阵的方式来存储图的边的信息//以下函数用于输入图的边的顶点信息和边的信息
void input(int *v,int arc[V][V]);//以下函数用于实现弗洛伊德算法void FloydAlgorithm(int v[V], int arc[V][V], int spath[V][V]);//以下函数用于输出两个顶点之间的最短路径间需要经过那些顶点，不包括源节点和目的节点
void output(int v[V], int spath[V][V], int start, int end);//以下函数用于打印图中任意两个结点之间的最短路径
void print_spath(int v[V], int arc[V][V], int spath[V][V]);int main()
{int vertex[V]; //用于存放图的顶点信息int ArcInfor[V][V]; //用于存放图的边的信息int spath[V][V]; //用于记录两个顶点之间的最短路径for (int i = 0; i < V; i++){for (int j = 0; j < V; j++){spath[i][j] = -1;}}//输入图的弧的信息和边的信息input(vertex, ArcInfor);//求最短路径FloydAlgorithm(vertex, ArcInfor, spath);return 0;}void input(int* v, int arc[V][V])
{printf("请输入图的顶点信息：\n");for (int i = 0; i < V; i++){scanf("%d", &v[i]);}printf("请输入图的边的信息：\n");for (int i = 0; i < V; i++){for (int j = 0; j < V; j++){scanf("%d", &arc[i][j]);}}}//以下函数用于输出两个顶点之间的最短路径间需要经过那些顶点，不包括源节点和目的节点
void output(int v[V],int spath[V][V],int start,int end) //start，end表示的是顶点所在的数组中的下标。
{//该函数需要用到递归思想，我们从右往左输出源节点到目的节点所经过的顶点的信息int k = spath[start][end]; //即从start到end中间需要经过的一个顶点再顶点数组中的下标if (k == -1){return;}output(v, spath, start, k);printf("%d->", v[k]);output(v, spath, k, end);
}//以下函数用于打印图中任意两个结点之间的最短路径
void print_spath(int v[V],int arc[V][V],int spath[V][V])
{for (int i = 0; i < V; i++){for (int j = 0; j < V; j++){if (i == j){continue;}else{if (arc[i][j] >= INF){printf("%d->%d之间不存在路径\n", v[i], v[j]);}else{printf("%d->%d之间的最短路径长度为：%d\n", v[i],v[j],arc[i][j]);printf("%d->%d之间的最短路径为:\n", v[i], v[j]);printf("%d->", v[i]);output(v, spath, i, j);printf("%d\n", v[j]);}}}}
}void FloydAlgorithm(int v[V],int arc[V][V],int spath[V][V])
{//只需要用到三重for循环即可实现弗洛伊德算法for (int k = 0; k < V; k++){for (int i = 0; i < V; i++){for (int j = 0; j < V; j++){if (arc[i][k] + arc[k][j] < arc[i][j]){arc[i][j] = arc[i][k] + arc[k][j];spath[i][j] = k;}}}}//打印最短路径print_spath(v, arc, spath);} 运行结果截图：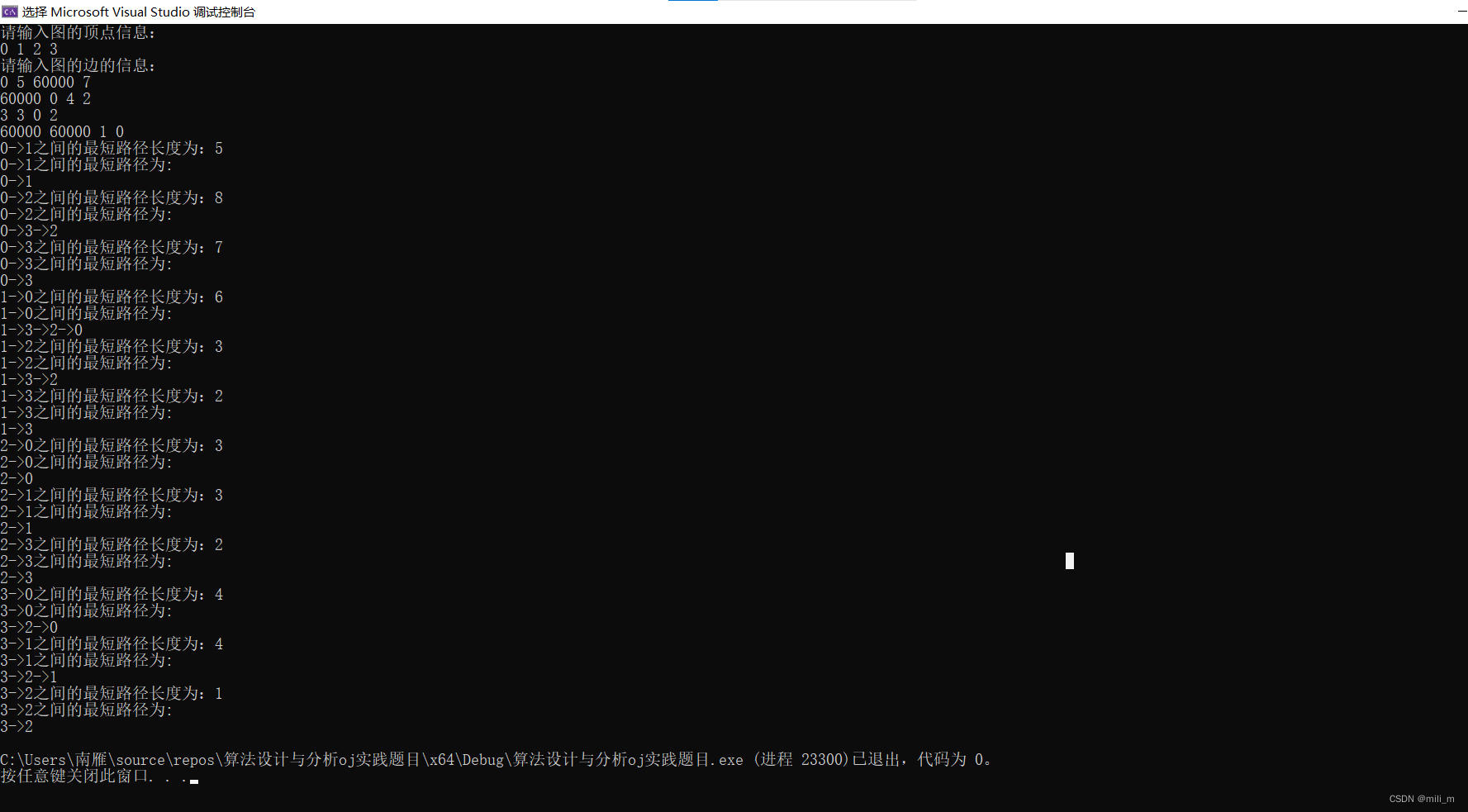
祝学习进步，生活愉快！
