Stable Diffusion — ControlNet 超详细讲解
ControlNet 最近非常火🔥!ControlNet 和 Stable Diffusion 的结合使 Stable Diffusion 能够接受指导图像生成过程的条件输入,从而增强了 Stable Diffusion 的性能。今天为大家深入剖析 ControlNet 的工作原理。

文章目录
- 什么是 ControlNet
- 内部架构
- 前馈
- 反向传播
- 与 Stable Diffusion 相结合
- 编码器
- 整体架构
- 训练
- 输入条件
- 总结
什么是 ControlNet
ControlNet 是一个控制预训练图像扩散模型(例如 Stable Diffusion)的神经网络。它允许输入调节图像,然后使用该调节图像来操控图像生成。
这里的调节图像类型众多,例如涂鸦、边缘图、姿势关键点、深度图、分割图、法线图等,这些输入都可以作为条件输入来指导生成图像的内容。 下面是一些例子:

内部架构

Stable Diffusion (UNet) 中的所有参数都被锁定并克隆到 ControlNet 端的可训练副本中。然后使用外部条件向量训练该副本。
创建原始权重的副本而不是直接训练原始权重是为了防止数据集较小时出现过拟合,并保持已经训练好的大模型的高质量,这些大模型在数十亿图像上训练得到,并可以直接部署到生产环境使用。
前馈

解释一下上图公式和符号:
- x , y x, y x,y:神经网络中的深层特征
- c c c:额外条件
- + + + : 特征相加
- Z ( ⋅ ; ⋅ ) \mathcal{Z}(\cdot\;;\;\cdot) Z(⋅;⋅):零卷积运算(权重和偏差都用零初始化的 1 x 1 卷积层)
- F ( ⋅ ; ⋅ ) \mathcal{F}(\cdot\;;\;\cdot) F(⋅;⋅):神经网络块操作(例如 “resnet” 块、“conv-bn-relu” 块等)
- Θ z 1 \Theta_{z1} Θz1:第一个零卷积层的参数
- Θ z 2 \Theta_{z2} Θz2:第二个零卷积层的参数
- Θ c \Theta_c Θc:可训练副本的参数
第一步训练

在第一步训练中,由于零卷积层的权重和偏差被初始化为零,因此前馈过程与没有 ControlNet 的过程相同。
经过反向传播后,ControlNet 中的零卷积层变为非零并影响输出。
换句话说,当 ControlNet 应用于某些神经网络块时,在进行任何优化之前,不会对深度神经特征造成任何影响。
反向传播

反向传播更新 ControlNet 中的可训练副本和零卷积层,使零卷积权重通过学习过程逐渐过渡到优化值。
为什么梯度不会为零?
我们可以假设如果卷积层的权重为零,则梯度为零。 然而,事实并非如此。
假设 y = w x + b y = wx + b y=wx+b 是零卷积层,其中 w w w 和 b b b 分别是权重和偏差, x x x 是输入特征图。以下是每一项的梯度。
y = w x + b ∂ y ∂ w = x ∂ y ∂ x = w ∂ y ∂ b = 1 y = wx+b\\ \frac{\partial y}{\partial w} = x \qquad \frac{\partial y}{\partial x} = w \qquad \frac{\partial y}{\partial b} = 1 y=wx+b∂w∂y=x∂x∂y=w∂b∂y=1
如果 w = 0 w=0 w=0 且 x ≠ 0 x \ne 0 x=0,则
∂ y ∂ w = x ≠ 0 ∂ y ∂ x = w = 0 ∂ y ∂ b = 1 ≠ 0 \frac{\partial y}{\partial w} = x \ne 0 \qquad \frac{\partial y}{\partial x} = w = 0 \qquad \frac{\partial y}{\partial b} = 1 \ne 0 ∂w∂y=x=0∂x∂y=w=0∂b∂y=1=0
回想一下梯度下降和链式法则:
w ← w − α ∂ L ∂ w w ← w − α ∂ L ∂ ⋅ … ∂ L ∂ w ⏟ ≠ 0 w \larr w-\alpha\frac{\partial \mathcal{L}}{\partial w}\\ w \larr w-\alpha\frac{\partial \mathcal{L}}{\partial \cdot}\dots\frac{\partial \mathcal{L}}{\underbrace{\partial w}_{\ne 0}} w←w−α∂w∂Lw←w−α∂⋅∂L…=0 ∂w∂L
一步训练之后, ∂ y ∂ x ≠ 0 \frac{\partial y}{\partial x} \ne 0 ∂x∂y=0。
一开始,当权重值 w = 0 w = 0 w=0 时,输入特征 x x x 通常不为0。结果,虽然 x x x 上的梯度由于零卷积而变为0,但权重和偏置的梯度不受影响。尽管如此,在一个梯度下降步骤之后,权重值 w w w 将更新为非零值(因为 y y y 对 w w w 的偏导数非零)。
与 Stable Diffusion 相结合
编码器
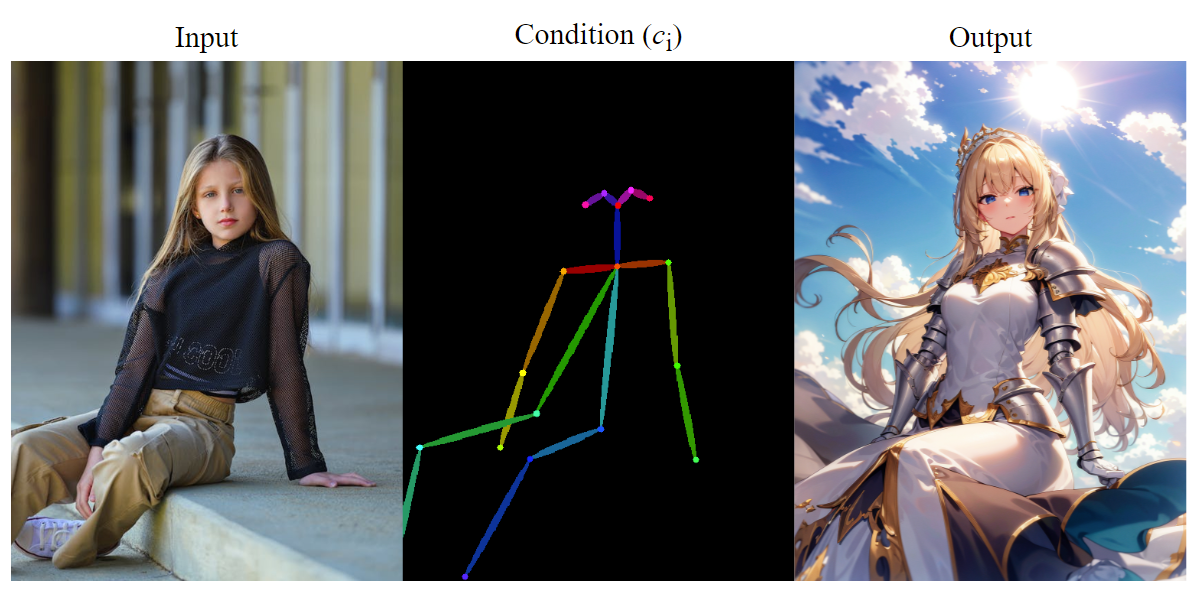
由于 Stable Diffusion 的 UNet 接受潜在特征 ( 64 × 64 64 \times 64 64×64) 而不是原始图像,因此我们还必须将基于图像的条件转换为 64 × 64 64 \times 64 64×64 的特征空间以匹配卷积大小。
c f = ε ( c i ) c_f = \varepsilon(c_i) cf=ε(ci)
我们可以使用网络 ε \varepsilon ε 将输入条件 c i c_i ci 编码为特征图 c f c_f cf。

上图中,我们使用 z t z_t zt 和 z t − 1 z_{t-1} zt−1 作为锁定网络块的输入和输出,以匹配 Stable Diffusion 上下文中的符号。
整体架构
下图展示了 Stable Diffusion 中 ControlNet 和 UNet 在一个去噪步骤中的输入和输出。

此外,下图从整体上说明了 ControlNet 和 Stable Diffusion 如何在反向扩散过程(采样)中协同工作。

上图是根据我之前关于 Stable Diffusion 的文章修改的。如果您还没有阅读过,建议您阅读 《Stable Diffusion 超详细讲解》 和 《Diffusion Model 深入剖析》。
训练
ControlNet 损失函数与 Stable Diffusion 的损失函数类似,但包含文本条件 c t c_t ct 和潜在条件 c f c_f cf,以提高输出与指定条件的一致性。
Stable Diffusion 损失函数:
L = E z 0 , t , ϵ [ ∥ ϵ − ϵ θ ( z t , t ) ∥ 2 ] \mathcal{L} = \mathbb{E}_{z_0,t,\epsilon}\big[\Vert \epsilon - \epsilon_\theta(z_t,t)\Vert^2\big] L=Ez0,t,ϵ[∥ϵ−ϵθ(zt,t)∥2]
Stable Diffusion + ControlNet 损失函数:
L = E z 0 , t , ϵ , c t , c f [ ∥ ϵ − ϵ θ ( z t , t , c t , c f ) ∥ 2 ] \mathcal{L} = \mathbb{E}_{z_0,t,\epsilon,\boxed{c_t,c_f}}\big[\Vert \epsilon - \epsilon_\theta(z_t,t,\boxed{c_t,c_f})\Vert^2\big] L=Ez0,t,ϵ,ct,cf[∥ϵ−ϵθ(zt,t,ct,cf)∥2]
作为训练过程的一部分,我们随机用空字符串替换 50% 的文本提示 c t c_t ct。这有助于 ControlNet 更好地理解输入条件图的含义,例如 Canny 边缘图或人类涂鸦。

通过删除提示,编码器被迫更多地依赖控制图中的信息,这提高了其理解其语义内容的能力。
输入条件
ControlNet 是一种灵活的工具,允许您使用不同类型的条件输入来加强 Stable Diffusion。以下是可在 ControlNet 中使用的输入类型。
Canny 边缘图

线条图

涂鸦

霍夫线

语义分割

深度图

法线图

姿势
总结
ControlNet 是一种神经网络,可以与预训练的扩散模型结合使用,特别是 Stable Diffusion 模型。
ControlNet 允许将条件输入(例如边缘图、分割图和关键点)包含到 Stable Diffusion 等大型扩散模型中。
结合 ControlNet 可以更好地控制图像生成过程,从而能够生成更具体、更符合要求的图像。