目录
题目:
示例:
分析:
代码:
题目:
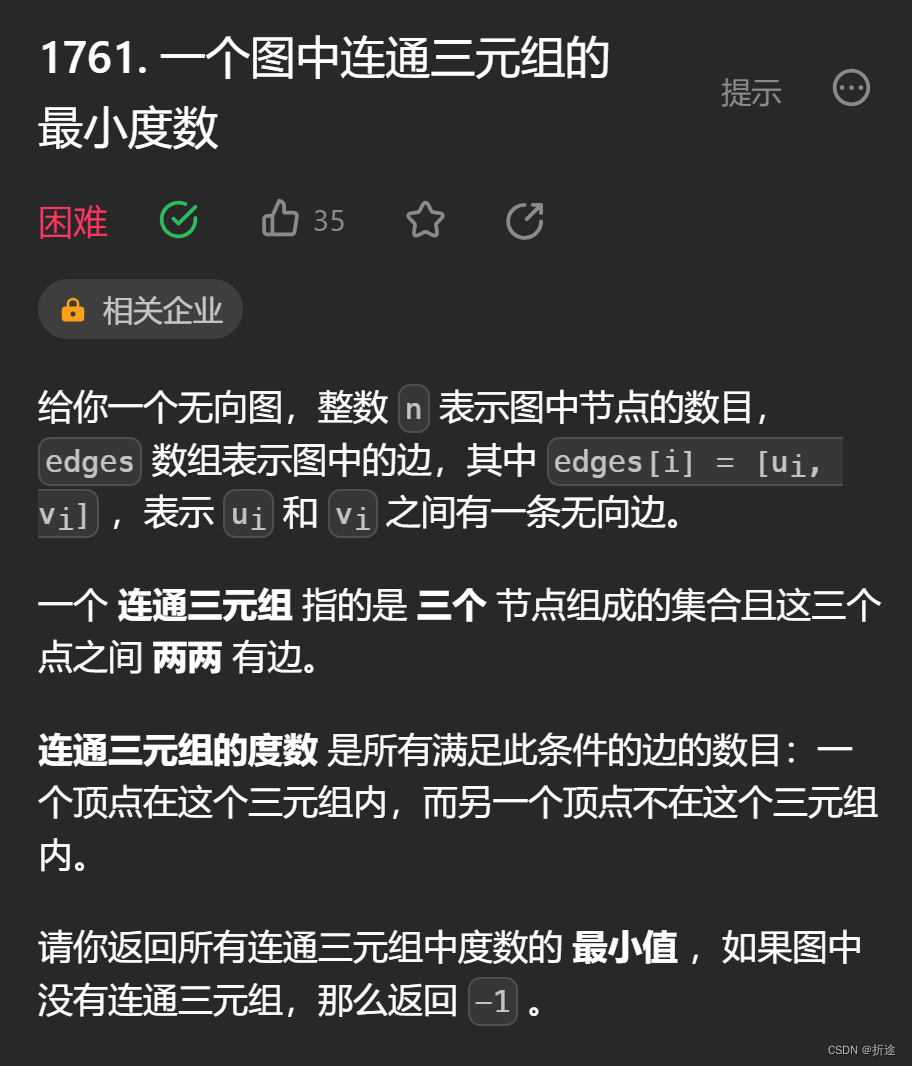
示例:
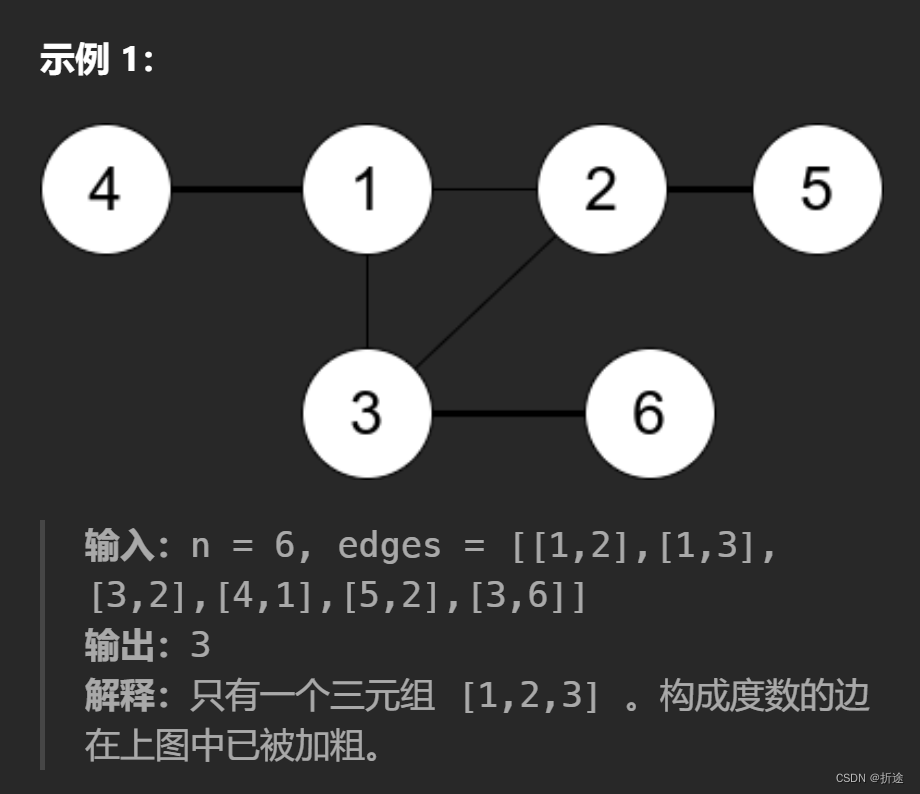
分析:
题目给我们一个无向图,要我们找出三个节点,这三个节点他们两两相连,这三个节点除了连接到对方的其他线被称为连通三元组的度数,问我们图中最小的三元组度数是多少。
我的第一个想法就是使用map来构建图,然后遍历每个节点,再遍历每个节点的相邻节点,再遍历每个节点的相邻节点的相邻节点,如果节点的相邻节点的相邻节点是该节点,那么我们就找到了连通三元组,他们总体的度数-6就是连通三元组的度数。因为三元组中每个节点为了连通另外两个节点,都需要花费两个度,而剩余的度就是连接其他非本三元组的节点了,所以连通三元组的度数就是三个节点的总度数-2*3。
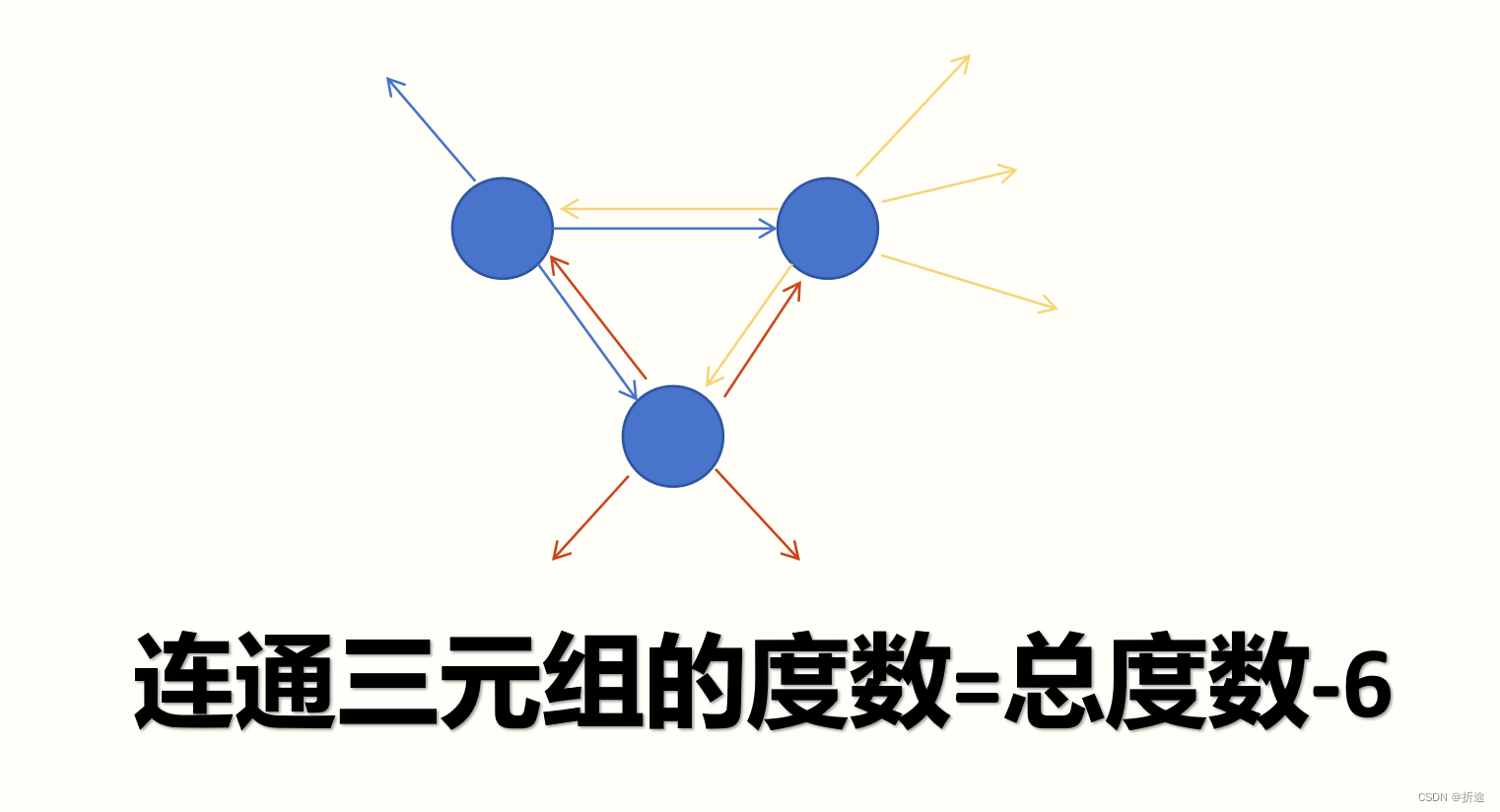
不过这么做就超时了,因为同一个三元组我们会重复遍历三次,每个节点我们都会遍历寻找包括它的连通三元组。虽然这种方式超时了,但也不失为一种方法,代码在下面,可以参考。
那么直接构建图不行,我们可以构建图的邻接矩阵。
我们另外再拿一个数组来存放每个节点的度数。
邻接矩阵用来判断三个点是否是相互连通的,度数数组用来计算连通三元组的度数。
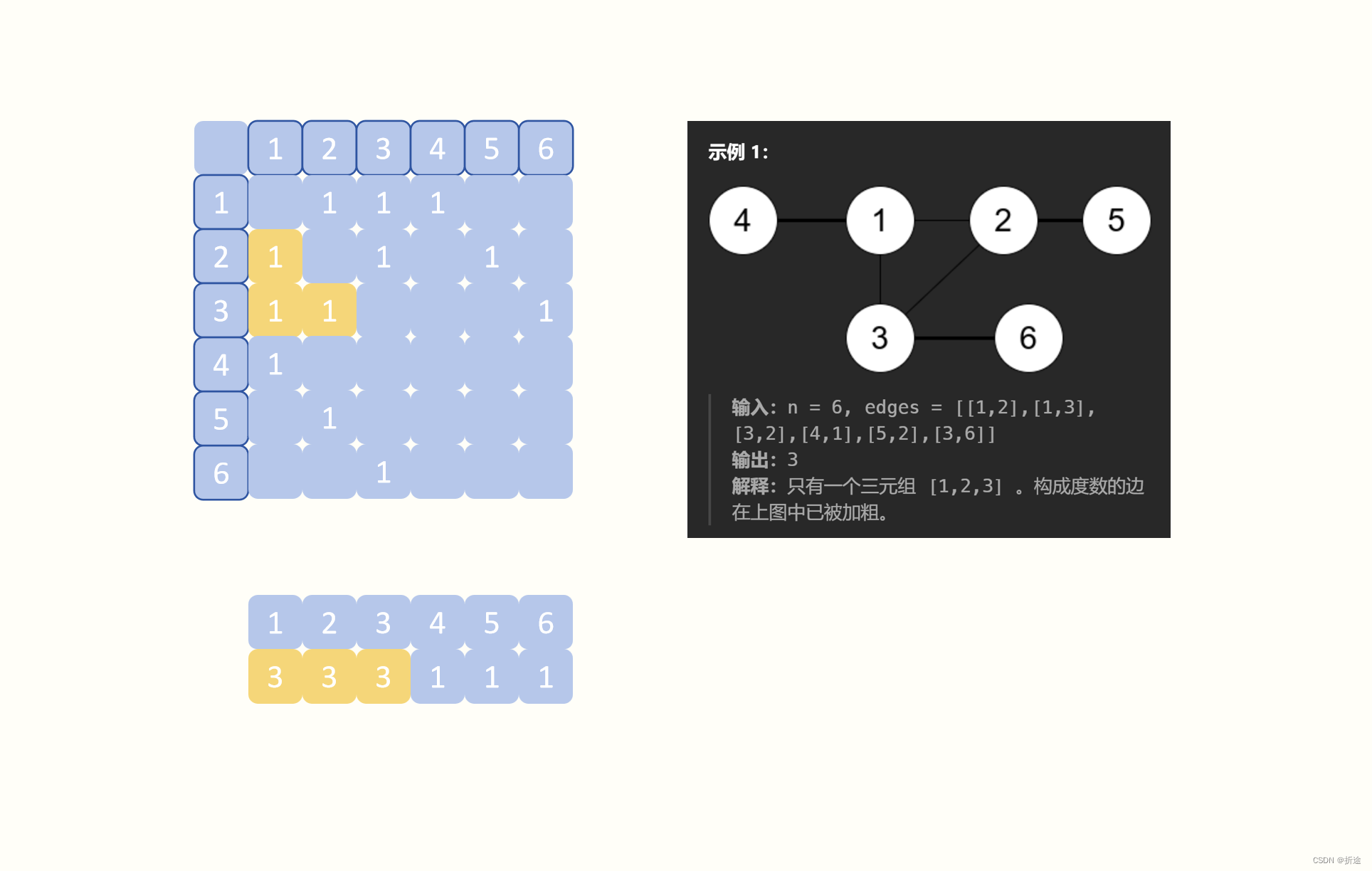
代码:
class Solution {
public:int minTrioDegree(int n, vector<vector<int>>& edges) {//超时unordered_map<int,unordered_set<int>>m;for(auto edge:edges){ //构建图if(m.find(edge[0])==m.end()) m[edge[0]]=unordered_set<int>();if(m.find(edge[1])==m.end()) m[edge[1]]=unordered_set<int>();m[edge[0]].insert(edge[1]);m[edge[1]].insert(edge[0]);}int res=INT_MAX;for(auto& i:m){ //取出每个节点for(auto& j: i.second){ //取出相连的节点集for(auto& k: m[j]){ //取出相连的节点的相连结果集if(m[k].count(i.first)){ //若是等于第一个节点,那么表示这仨节点相互连通res=min(res,static_cast<int>(i.second.size()+m[j].size()+m[k].size()-6));}}}}return res==INT_MAX?-1:res;//构建邻接矩阵 int res=INT_MAX;vector<vector<int>>pic(n+1,vector<int>(n+1,0)); //连通矩阵vector<int>du(n+1,0); //每个点的度for(auto& edge: edges){ //构建邻接矩阵以及获取每个节点的度pic[edge[0]][edge[1]]=1;pic[edge[1]][edge[0]]=1;du[edge[0]]++;du[edge[1]]++;} for(int i=1;i<=n;i++){ for(int j=i+1;j<=n;j++){for(int k=j+1;k<=n;k++){//遍历每个节点,找到相互连通的三个节点,度数之和-6就是连通三元组的读度数if(pic[i][j] && pic[j][k] && pic[i][k]) res=min(res,du[i]+du[j]+du[k]-6);}}}return res==INT_MAX?-1:res;}
};