一：形态滤波

（1）概述

形态滤波：是一种在数字图像处理中常用的图像处理技术，用于改善图像的质量、提取图像的特定特征或去除图像中的噪声。形态滤波主要基于形态学运算，通过结构元素（也称为模板）对图像进行局部区域的操作，从而改变图像的形状和结构。选择不同形状(如各向同性的圆、十字架、矩形、不同朝向的有向线段等)、不同尺寸的结构元素可以提取图像的不同特征

（2）程序

如下：实现对二值图像的特征提取

---

matlab实现：

I=imread(‘pattern.jpg’);
BW1=im2bw(I,h);
BW1=1-BW1;
se=strel('square',3); 
BW2=1-imopen(BW1,se);
figure;imshow(BW2);title('矩形块提取');
se45=strel('line',25,45);     
BW3=1-imopen(BW1,se45);
figure;imshow(BW3);title('线段提取');

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像
I = cv2.imread('pattern.jpg', cv2.IMREAD_GRAYSCALE)# 二值化处理
_, BW1 = cv2.threshold(I, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
BW1 = 255 - BW1# 矩形块提取
se = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
BW2 = cv2.morphologyEx(BW1, cv2.MORPH_OPEN, se)
BW2 = 255 - BW2# 显示矩形块提取结果
plt.imshow(BW2, cmap='gray')
plt.title('矩形块提取')
plt.show()# 线段提取
se45 = cv2.getStructuringElement(cv2.MORPH_RECT, (25, 25))
se45 = cv2.rotate(se45, cv2.ROTATE_90_CLOCKWISE)
BW3 = cv2.morphologyEx(BW1, cv2.MORPH_OPEN, se45)
BW3 = 255 - BW3# 显示线段提取结果
plt.imshow(BW3, cmap='gray')
plt.title('线段提取')
plt.show()

二：图像的平滑处理

（1）概述

图像的平缓处理：是数字图像处理中的一项重要任务，它有助于减少图像中的噪声和细节，并使图像更加平滑和连续。通过结合开运算和闭运算，可以实现图像的更加全面的平滑处理。首先，使用开运算可以消除细小的噪声和不连续区域，平滑边缘，同时保留较大的结构。接着，使用闭运算可以填补空洞，连接区域，消除缺陷和断裂，使图像更加连续和平滑。对二值图像平滑处理的形态学变换为

$$\begin{array}{l}\mathbf{Y}=(\mathbf{X}\circ \mathbf{S})\cdot \mathbf{S}\\ \mathbf{Y}=(\mathbf{X}\cdot \mathbf{S})\circ \mathbf{S}\end{array}$$

例如下图，结构元素$S$大于所有噪声和噪声块的尺寸

（2）程序

如下

---

matlab实现：

Image=imread('A.bmp');
BW=im2bw(Image);
SE=strel('square',3);
result1=imclose(imopen(BW,SE),SE); 
figure,imshow(result1);
result2=imopen(imclose(BW,SE),SE);               
figure,imshow(result2);

Python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像
Image = cv2.imread('A.bmp', cv2.IMREAD_GRAYSCALE)# 二值化处理
_, BW = cv2.threshold(Image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)# 创建结构元素
SE = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))# 先开运算再闭运算
result1 = cv2.morphologyEx(cv2.morphologyEx(BW, cv2.MORPH_OPEN, SE), cv2.MORPH_CLOSE, SE)# 显示结果1
plt.imshow(result1, cmap='gray')
plt.show()# 先闭运算再开运算
result2 = cv2.morphologyEx(cv2.morphologyEx(BW, cv2.MORPH_CLOSE, SE), cv2.MORPH_OPEN, SE)# 显示结果2
plt.imshow(result2, cmap='gray')
plt.show()

三：图像的边缘提取

（1）概述

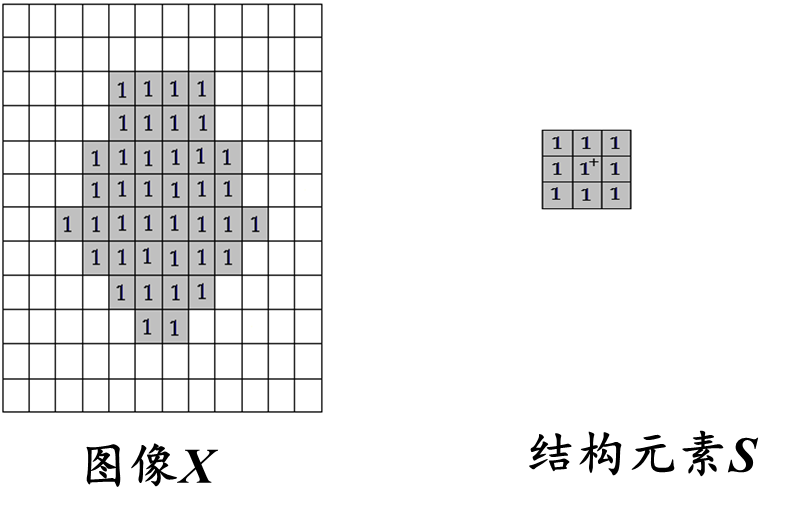
图像的边缘提取：是数字图像处理中的一项重要任务，它有助于凸显图像中的边缘和轮廓信息，以便于进一步的分析和处理。结合开运算和闭运算可以实现图像的边缘提取。首先，应用闭运算可以填补图像中的空洞和断裂，连接边缘区域，使边缘更加连续。然后，应用开运算可以平滑边缘、去除细小的孤立点和细线条，突出边缘特征。提取物体的轮廓边缘的形态学变换

• 内边界：$\mathbf{Y}=\mathbf{X}-(\mathbf{X}\ominus \mathbf{S})$
• 外边界：$\mathbf{Y}=(\mathbf{X}\oplus \mathbf{S})-\mathbf{X}$
• 形态学梯度：$\mathbf{Y}=(\mathbf{X}\oplus \mathbf{S})-(\mathbf{X}\ominus \mathbf{S})$

例如下图，使用结构元素$S$对图像$X$进行边缘提取

（2）程序

如下

---

matlab实现：

Image=imread('menu.bmp');
BW=im2bw(Image);
SE=strel('square',3);
result1=BW-imerode(BW,SE); 
result2=imdilate(BW,SE)-BW; 
result3=imdilate(BW,SE)-imerode(BW,SE);     
figure,imshow(result1);
figure,imshow(result2);
figure,imshow(result3);

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像
Image = cv2.imread('menu.bmp', cv2.IMREAD_GRAYSCALE)# 二值化处理
_, BW = cv2.threshold(Image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)# 创建结构元素
SE = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))# 边缘提取结果1
result1 = BW - cv2.erode(BW, SE)# 显示结果1
plt.imshow(result1, cmap='gray')
plt.show()# 边缘提取结果2
result2 = cv2.dilate(BW, SE) - BW# 显示结果2
plt.imshow(result2, cmap='gray')
plt.show()# 边缘提取结果3
result3 = cv2.dilate(BW, SE) - cv2.erode(BW, SE)# 显示结果3
plt.imshow(result3, cmap='gray')
plt.show()

四：区域填充

（1）概述

概述：是数字图像处理中的一项常见任务，它有助于填补图像中的空洞或断裂，并连接相邻的区域，使图像中的区域变得连续和完整。结合开运算和闭运算可以实现图像的区域填充。首先，通过应用开运算，可以去除图像中的小型空洞、断裂和孤立点，使得区域边缘更加连续。接着，再应用闭运算，可以填补空洞、连接区域，使得图像中的区域变得完整和连续

$$X_k=\left(X_{k-1}⨁S\right)\cap A^C,k=1,2,3,\cdots$$

如下图，边界点用灰色表示，赋值为1；所有非边界点是白色部分，赋值为0

（2）程序

如下

---

matlab实现：

Image=imread('coin.bmp');
BW=im2bw(Image);
imshow(BW); title('二值图像');
result1=imfill(BW,'holes');
figure,imshow(result1);title('二值图像的区域填充');

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像
Image = cv2.imread('coin.bmp', cv2.IMREAD_GRAYSCALE)# 二值化处理
_, BW = cv2.threshold(Image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)# 显示二值图像
plt.imshow(BW, cmap='gray')
plt.title('二值图像')
plt.show()# 区域填充
result1 = cv2.fillHoles(BW)# 显示区域填充结果
plt.imshow(result1, cmap='gray')
plt.title('二值图像的区域填充')
plt.show()

五：目标探测（击中与否变换）

（1）概述

目标探测（击中与否变换）：击中与否变换的原理利用腐蚀特性——腐蚀的过程相当于对可以填入结构元素的位置作标记的过程。目标检测既要检测目标内部，也要检测外部，即在一次运算中要同时捕获内外标记。因此，进行目标探测，需要采用两个结构元素$S_1$、$S_2$，构成一个结构元素对$S=(S_1,S_2)$

• $S_1$：探测目标内部
• $S_2$：探测目标外部

则图像$X$用结构元素$S$进行击中与否变换，记为

$$\begin{array}{l}\mathbf{X}\ast \mathbf{S}=\left(\mathbf{X}\ominus {\mathbf{S}}_1\right)\cap \left({\mathbf{X}}^{\mathbf{C}}\ominus {\mathbf{S}}_2\right)\\ \mathbf{X}\ast \mathbf{S}=\left(\mathbf{X}\ominus {\mathbf{S}}_1\right)\cap \left({\mathbf{X}}^{\mathbf{C}}⨁{\hat{\mathbf{S}}}_2\right)\\ \mathbf{X}\ast \mathbf{S}=\left\{\mathbf{x}\mid {\mathbf{S}}_1+\mathbf{x}\subseteq \mathbf{X}\text{ and }{\mathbf{S}}_2+\mathbf{x}\subseteq {\mathbf{X}}^{\mathbf{C}}\right\}\end{array}$$

当且仅当结构元素$S_1$平移到某一点可填入集合$X$的内部，结构元素$S_2$平移到该点可填入集合 的外部时，该点才在击中击不中变换的输出中

例如下图，(a)为由四个物体：矩形、小方形、大方形、带有小凸出部分的大方形组成的图像$X$；(b)为结构元素对$S=(S_1,S_2)$。要求通过击中与否运算，能正确识别方形

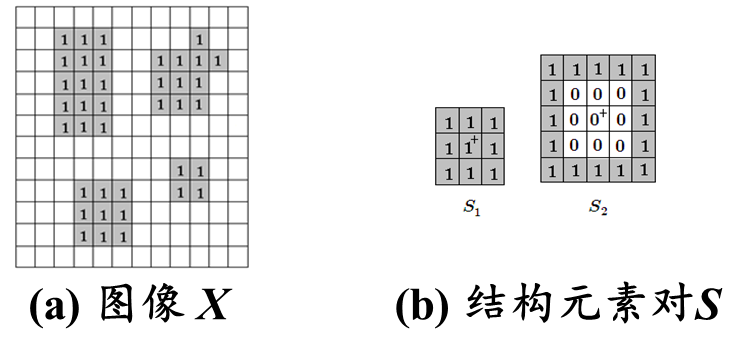
效果如下

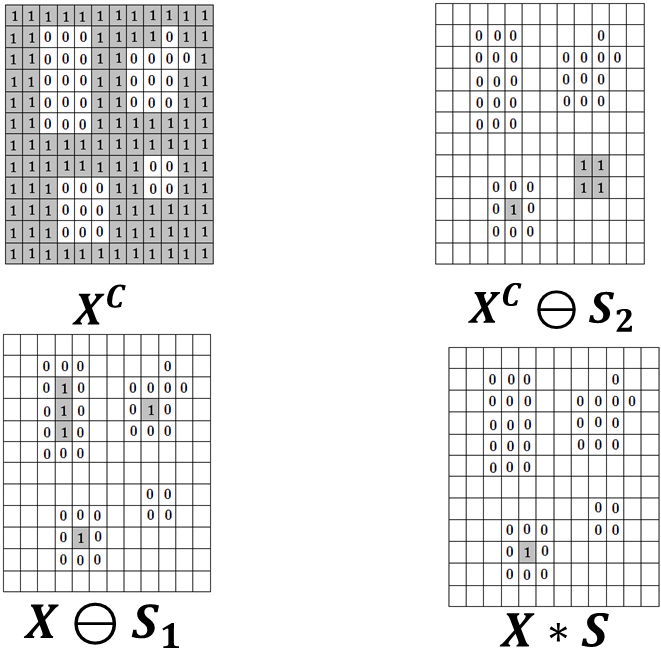
（2）程序

如下

---

matlab实现：

Image=imread('test.bmp');
BW=im2bw(Image);                 
interval=[-1  -1  -1  -1  -1-1  -1  -1  -1  -1-1  -1  1   1   1-1  -1  1   1   1-1  -1  1   1   1];      %定义结构元素对
result=bwhitmiss(BW,interval);   %击中击不中
figure,imshow(result); title('击中与否变换结果');

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像
Image = cv2.imread('coin.bmp', cv2.IMREAD_GRAYSCALE)# 二值化处理
_, BW = cv2.threshold(Image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)# 显示二值图像
plt.imshow(BW, cmap='gray')
plt.title('二值图像')
plt.show()# 区域填充
result1 = cv2.fillHoles(BW)# 显示区域填充结果
plt.imshow(result1, cmap='gray')
plt.title('二值图像的区域填充')
plt.show()

六：细化

（1）概述

细化：骨架化结构是目标图像的重要拓扑描述。对目标图像进行细化处理，就是求图像的中央骨架的过程，是将图像上的文字、曲线、直线等几何元素的线条沿着其中心轴线将其细化成一个像素宽的线条的处理过程。基于数学形态学变换的细化算法为

$$\mathbf{X}\odot \mathbf{S}=\mathbf{X}-(\mathbf{X}\ast \mathbf{S})$$

可见，细化实际上为从集合$X$中去掉被结构元素$S$击中的结果。具体采用的细化方法为

$${\mathbf{X}}_1=\mathbf{X}\odot \mathbf{S},{\mathbf{X}}_2={\mathbf{X}}_1\odot \mathbf{S},\cdots \cdots {\mathbf{X}}_n={\mathbf{X}}_{n-1}\odot \mathbf{S}$$

如下示例

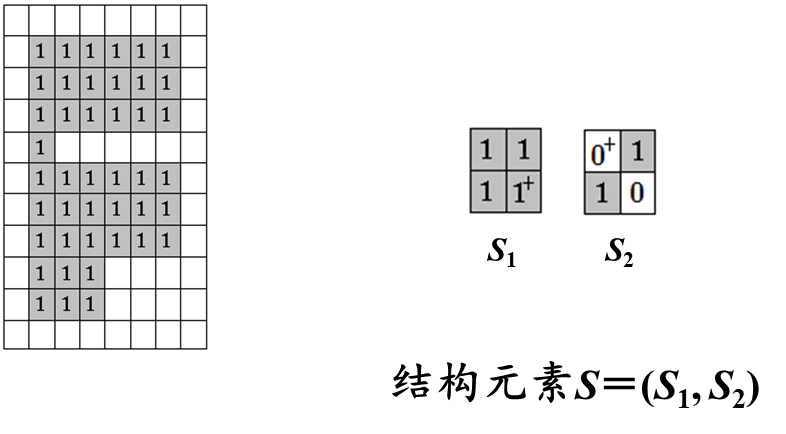
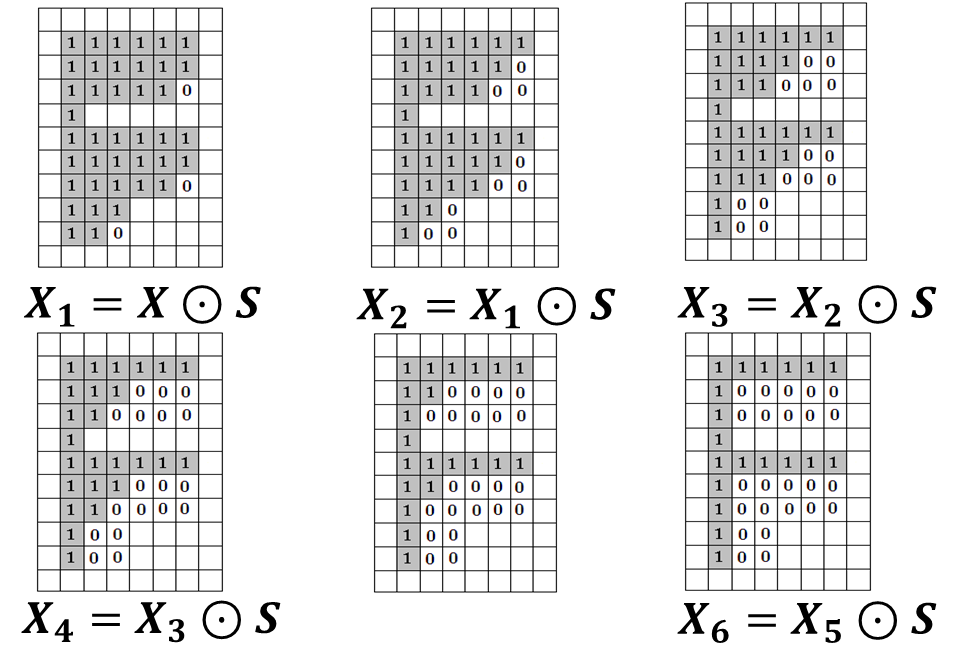
（2）程序

如下

---

matlab实现：

Image=imread('menu.bmp');
BW=im2bw(Image); 
result1=bwmorph(BW,'thin',1); 
result2=bwmorph(BW,'thin',Inf); 
figure,imshow(result1);title('细化一次');
figure,imshow(result2);title('细化至只有一个像素宽');

python实现：

Image=imread('menu.bmp');
BW=im2bw(Image); 
result1=bwmorph(BW,'thin',1); 
result2=bwmorph(BW,'thin',Inf); 
figure,imshow(result1);title('细化一次');
figure,imshow(result2);title('细化至只有一个像素宽');