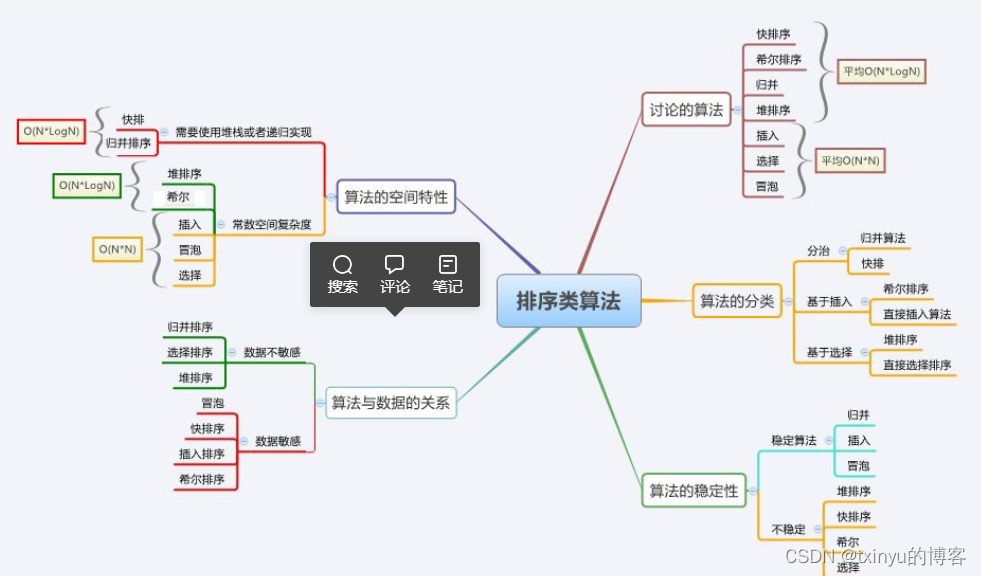
目录
选择排序-直接插入排序
插入排序-希尔排序
选择排序-简单选择排序
选择排序-堆排序
交换排序-冒泡排序
交换排序-快速排序
归并排序
基数排序
选择排序-直接插入排序
基本思想:
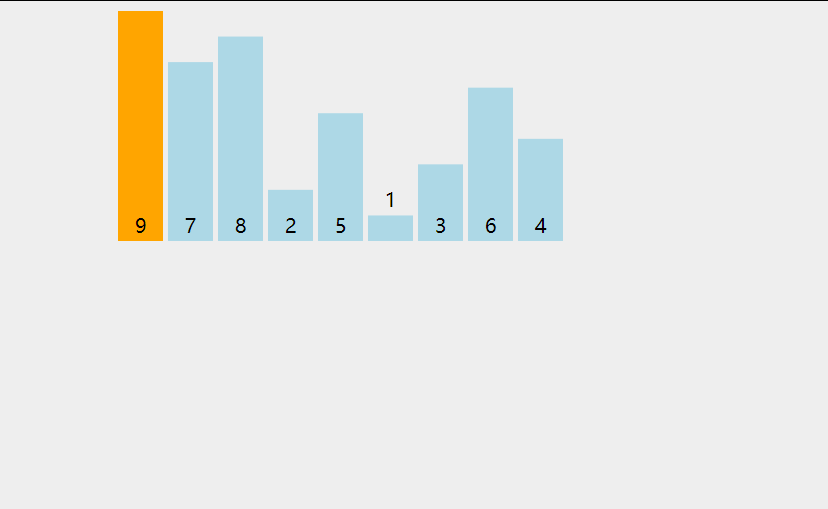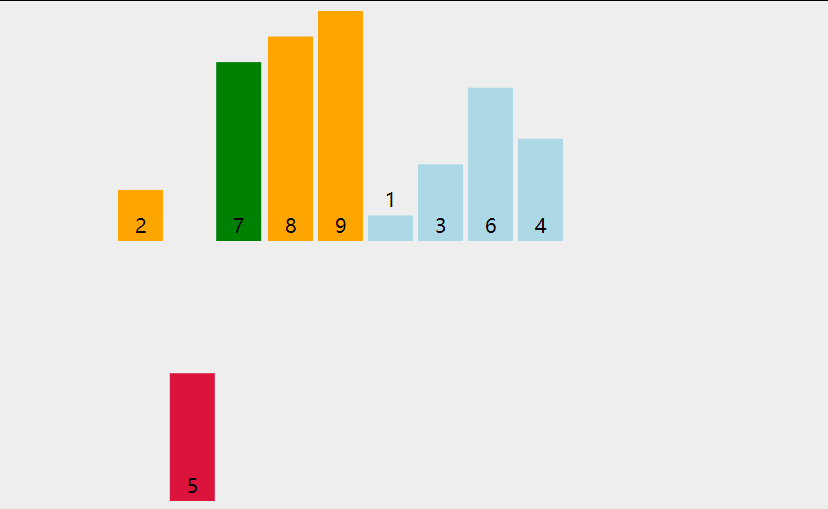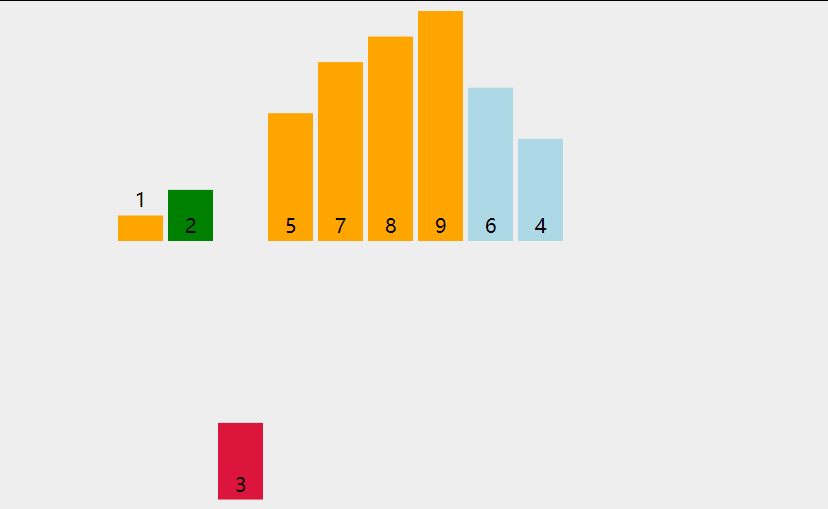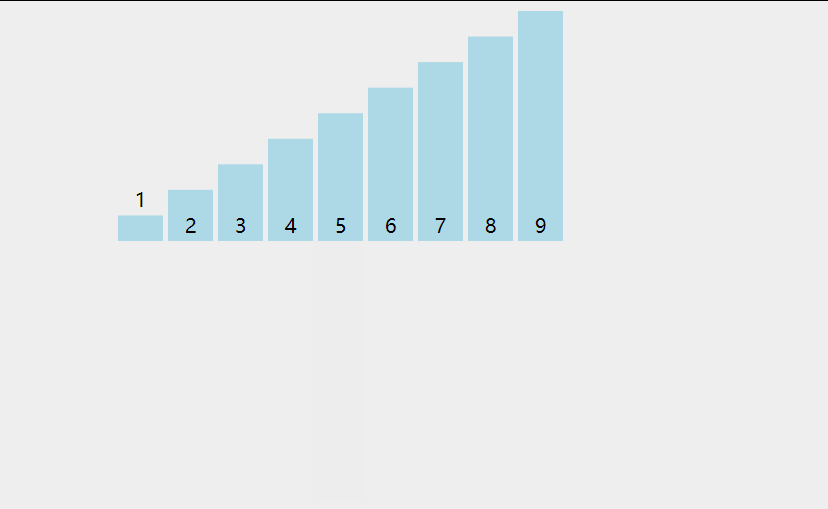
如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
具体代码实现:
void InsertSort(int* const arr, const int len)
{assert(arr);for (int i = 0; i < len; i++)//遍历每个元素{for (int j = i; j > 0; j--)//与前面的元素相比较{if (arr[j] < arr[j - 1])swap(arr + j, arr + j - 1);else //已经有序break;}}
}复杂度分析:
时间复杂度O(N^2),空间复杂度O(1)
插入排序是一种稳定的排序算法,当元素集合越接近有序,直接插入排序算法的时间效率越高。
插入排序-希尔排序
基本思想: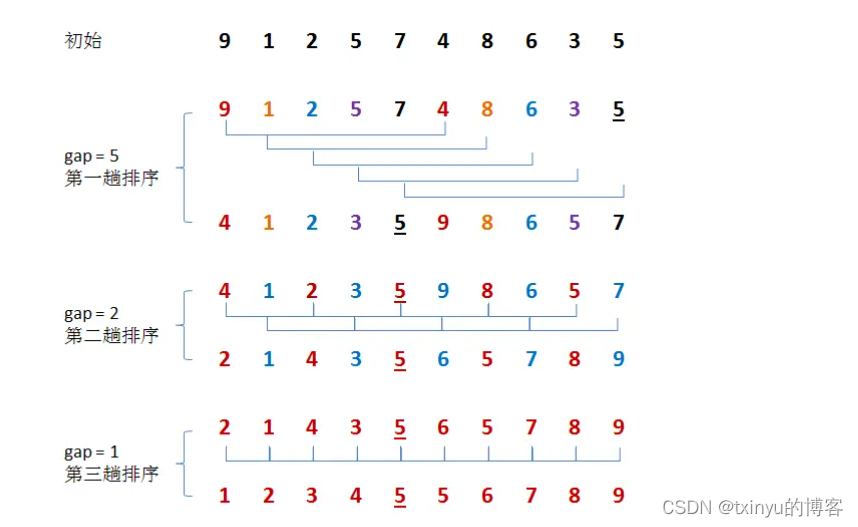
对待排序数组中的元素进行分组,从第一个元素开始,按照数组下标中间隔为gap大小的元素分为一组,对每一组进行排序,重新选择gap的大小使得原始数据更加有序,当gap=1的时候就是插入排序。
代码实现:
void ShellSort(int* const arr, const int len)
{int gap = len;while (gap > 1){gap = gap / 3 + 1;//调整gap的大小,gap=1的时候,为插入排序for (int i = gap; i < len; i++)//总共只需要循环len-gap次{for (int j = i; j >= gap; j-=gap)//插入排序{if (arr[j] < arr[j - gap]){swap(arr + j, arr + j - gap);}elsebreak;}}}
}这里的分组比较不是分开进行的(第一组比完第二组在比),而是多组同时进行比较,从第gap个元素开始,逐渐往前比较,每次和自己和自己gap距离的元素比较
复杂度分析:O(N^1.3 - N^2)
稳定性:不稳定
选择排序-简单选择排序
基本思想:
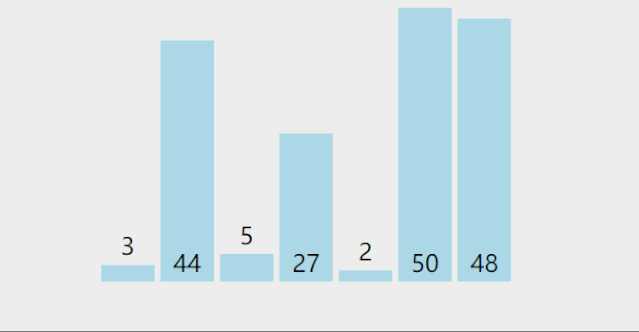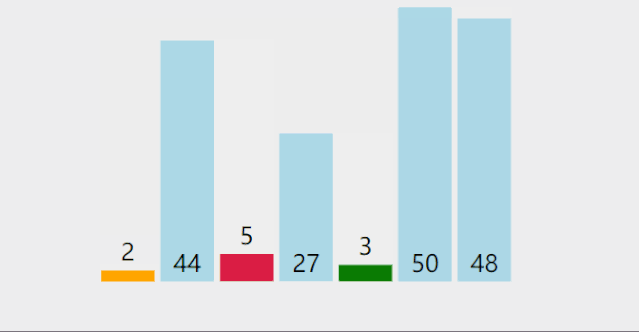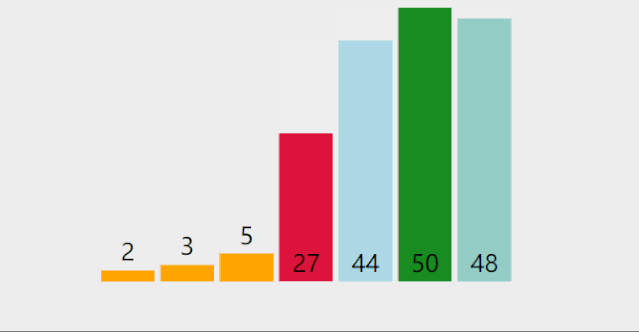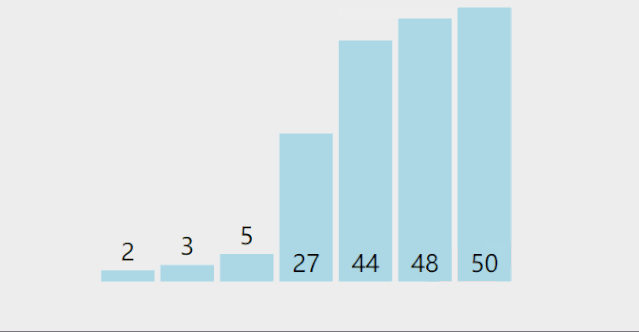
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序数据元素排完.
代码实现:
void SelectSort(int*a,int n)
{int left=0;while(left<n){int min=left; for(int i=left;i<n;i++)//找最小值 {if(a[min]>a[i]){min=i;}}Swap(&a[left],&a[min]);//交换数据 然后找次小,交换 left++; }
} 时间复杂度O(n^2),空间复杂度O(1);不稳定
选择排序-堆排序
基本思想:
堆排序是基于数据结构堆设计的一种排序算法,通过堆来选择数据,向上(向下)调整,得到小数(大数),然后再与堆底数据进行交换,即可排序,需要注意的是排升序建大堆,排降序建小堆
代码实现:
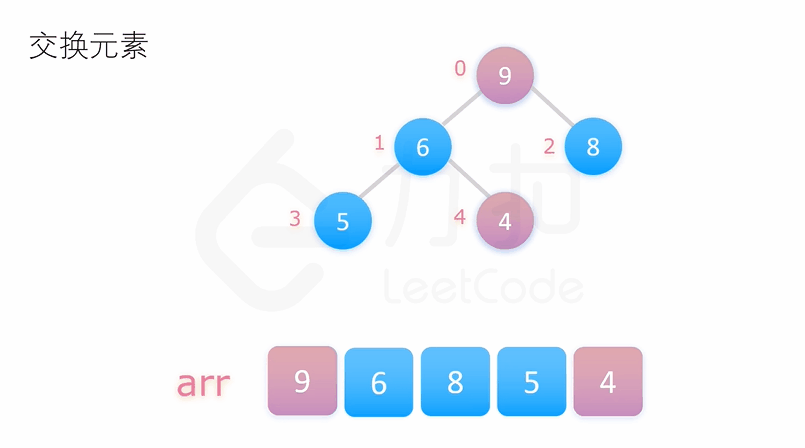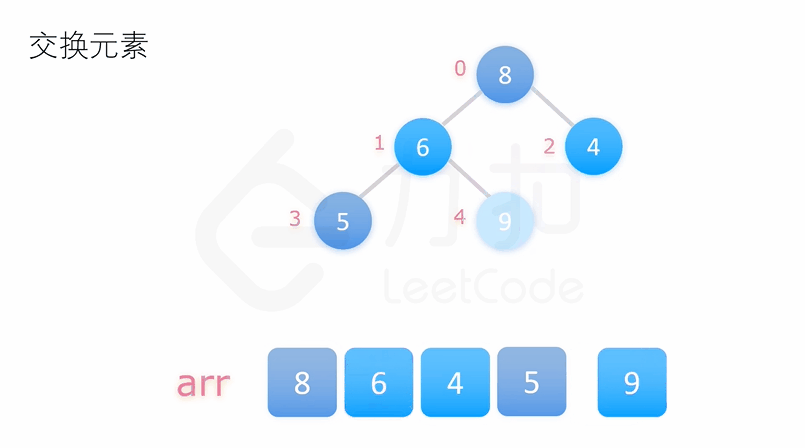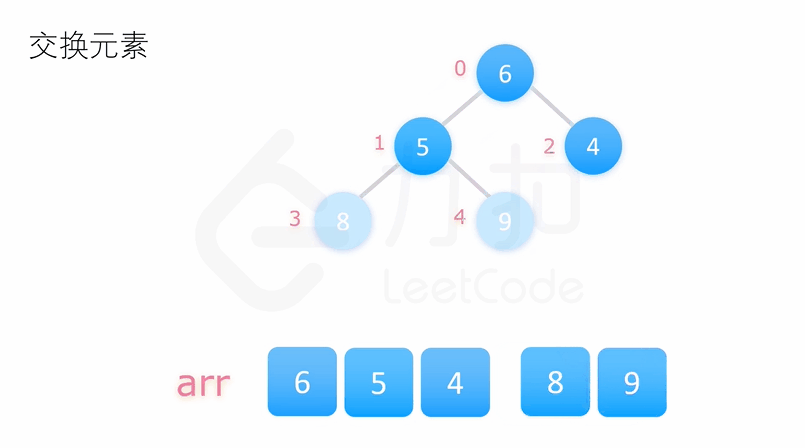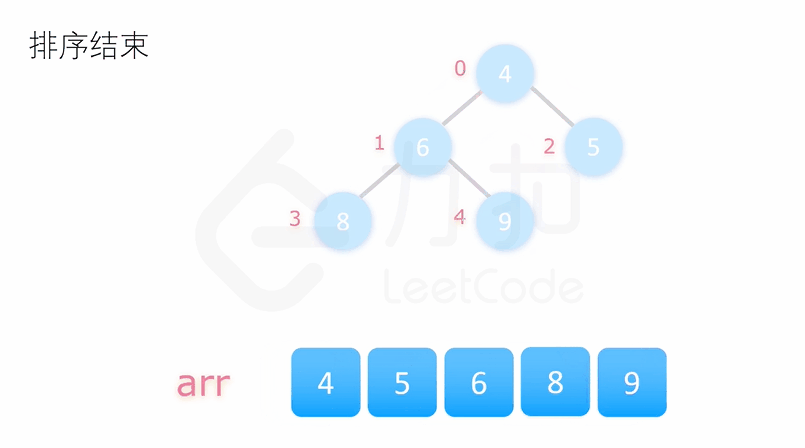
代码实现:
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDwon(int* a, int n, int root)
{int parent = root;int child = parent * 2 + 1;//找到孩子while (child < n){if (child + 1 < n && a[child + 1] > a[child])//考虑右孩子越界和判断那个孩子大{++child;}if (a[child] > a[parent])//判断孩子和父亲谁大,孩子大,向上交换{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{// 升序 建大堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDwon(a, n, i);}int end = n - 1;//向下调整,交换while (end > 0){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);--end;}
}时间复杂度O(n*logn),空间复杂度O(1); 不稳定
交换排序-冒泡排序
基本思想: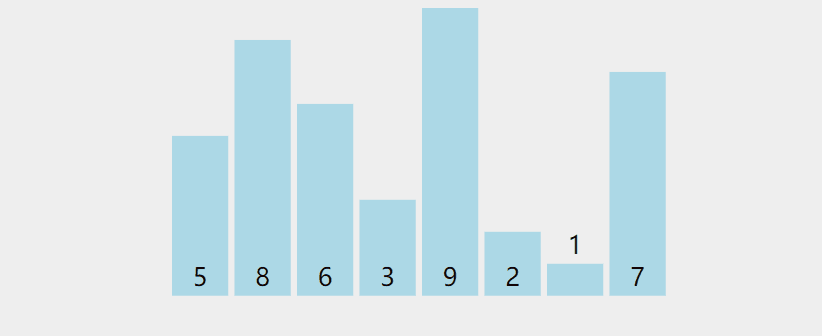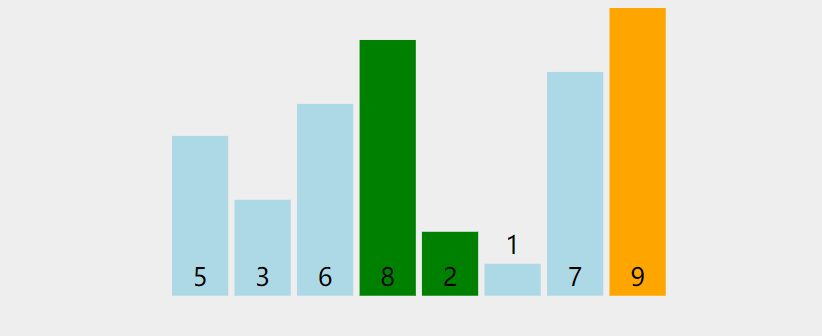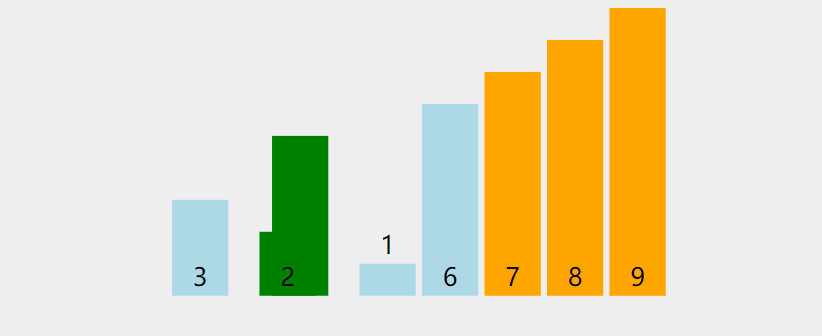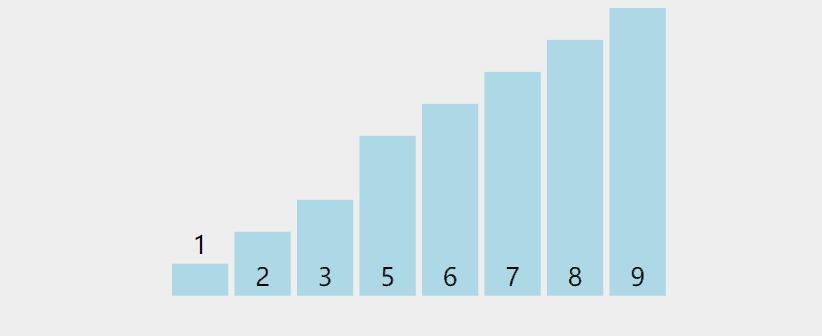
代码实现:
//冒泡排序
void Bubblesort(int *a,int n)
{for(int i=0;i<n;i++)//控制交换次数 {for(int j=0;j<n-i-1;j++)//向后冒泡 ,控制边界 {if(a[j]>a[j+1])//如果前一个值大于后一个值,交换. {swap(&a[j],&a[j+1]);} }}
} 时间复杂度O(n^2),空间复杂度O(1) 稳定
交换排序-快速排序
基本思想:
代码实现:
int PartSort1(int* a, int left, int right)
{int keyi = left;while (left < right){// 找小while (left < right && a[right] >= a[keyi])--right;// 找大while (left < right && a[left] <= a[keyi])++left;swap(&a[left], &a[right]);//交换左右值}swap(&a[keyi], &a[left]);//最后交换key与leftreturn left;//返回当前节点,[0,left-1],[left+1,right]递归排序
}快排优化:
若初始序列按关键码有序或基本有序时,快排序反而蜕化为冒泡排序。为改进之,通常以“三者取中法”来选取基准记录,即将排序区间的两个端点与中点三个记录关键码居中的调整为支点记录,本质在于防止最坏的情况发生(1,已经有序2,数据全部相等)
为了避免这种情况,选取头尾和中间元素,比较大小,找大小处于中间的元素为key值,实现对快排的优化,时间复杂度仍为O(nlog^n),每次调用排序的时候把key置一下.
//快排三数优化
int GetMid(int* a, int left, int right)
{int mid = (left + right) >> 1;// left mid rightif (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;} }else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}时间复杂度:O(N*logN) 空间复杂度:O(N*logN) 不稳定
归并排序
基本思想:

代码实现:
//归并排序
void merge(int*a,int*arr,int left,int mid,int right)
{//标记左半区第一个未排序的元素int l_pos=left; //标记右半区第一个未排序的元素int r_pos=mid+1;//临时数组下标的元素 int pos=left;//合并while(l_pos<=mid&&r_pos<=right){if(a[l_pos]<a[r_pos])arr[pos++]=a[l_pos++];elsearr[pos++]=a[r_pos++];} //合并左半区剩余的元素while(l_pos<=mid){arr[pos++]=a[l_pos++];}//合并右半区剩余的元素while(r_pos<=right){arr[pos++]=a[r_pos++];}//把临时数组合并后的元素复制到a中 while(left<=right){a[left]=arr[left];left++;}
}时间复杂度:O(N*logN) 空间复杂度:O(N) 稳定性:稳定
基数排序
基本思想:
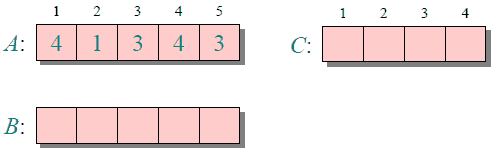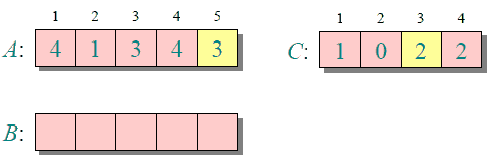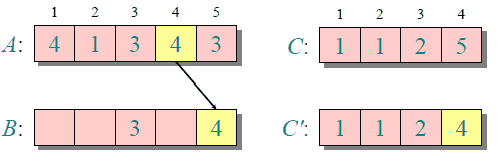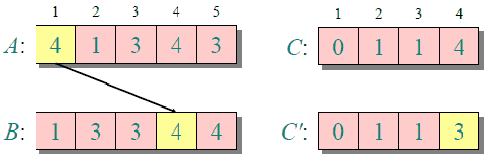
代码实现:
void CountSort(int* a, int n)
{int max = a[0], min = a[0];for (int i = 0; i < n; ++i){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}int range = max - min + 1;int* count = malloc(sizeof(int)*range);memset(count, 0, sizeof(int)*range);for (int i = 0; i < n; ++i)//计数 {count[a[i] - min]++;}int i = 0;for (int j = 0; j < range; ++j)//排序 {while (count[j]--){a[i++] = j + min;}}free(count);
}时间复杂度:O(MAX(N,范围)) 空间复杂度:O(范围) 稳定性:稳定
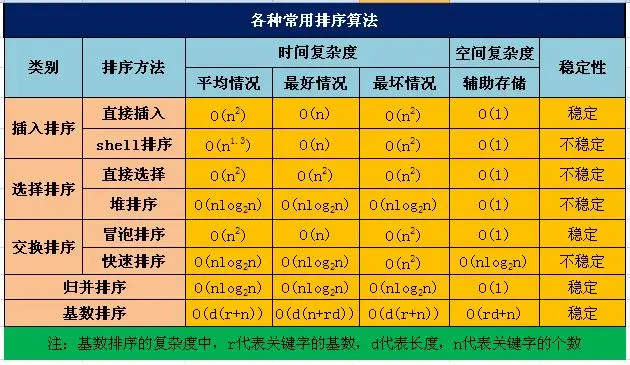
排序算法复杂度及稳定性分析