Laplacian算子是一种图像处理中常用的边缘检测算子,它用于检测图像中的边缘和轮廓。该算子计算图像中每个像素点的二阶导数,从而突出图像中灰度值变化较大的区域,这些区域通常对应图像的边缘或者轮廓。
Laplacian(拉普拉斯)算子是一种二阶导数算子,其具有旋转不变性,可以满足不同方向
的图像边缘锐化(边缘检测)的要求。通常情况下,其算子的系数之和需要为零。
Laplacian算子的一种常用形式是二维离散Laplacian算子,表示为:
0 1 01 -4 10 1 0
该算子是一个3x3的矩阵,它对应的是图像中每个像素点的上、下、左、右四个方向的像素值以及像素点本身的像素值之间的差值。
应用Laplacian算子的过程如下:
- 将3x3的Laplacian算子依次对图像中的每个像素点进行卷积操作。
- 将卷积结果作为图像的每个像素点的新像素值。
- 对于卷积结果,如果像素值较大,则表示该像素点周围灰度值变化较大,可能是图像中的边缘或轮廓。
Laplacian 算子类似二阶 Sobel 导数,需要计算两个方向的梯度值。例如,在图 9-25 中:
- 左图是 Laplacian 算子。
- 右图是一个简单图像,其中有 9 个像素点。
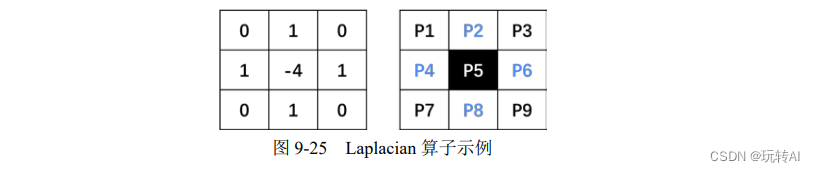
计算像素点 P5 的近似导数值,如下:
P5lap = (P2 + P4 + P6 + P8) - 4·P5
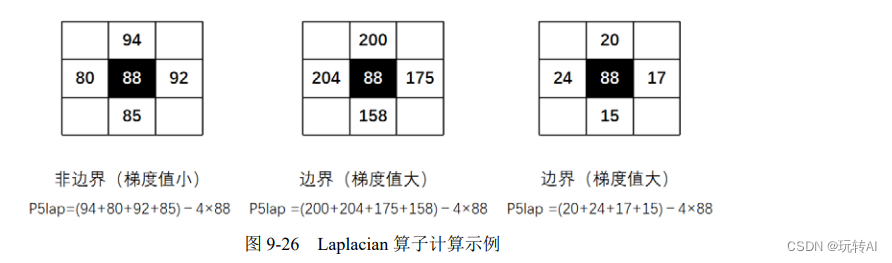
图 9-26 展示了像素点与周围点的一些实例,其中:
- 在左图中,像素点 P5 与周围像素点的值相差较小,得到的计算结果值较小,边缘不明显。
- 在中间的图中,像素点 P5 与周围像素点的值相差较大,得到的计算结果值较大,边缘较明显。
- 在右图中,像素点 P5 与周围像素点的值相差较大,得到的计算结果值较大,边缘较明显。
需要注意,在上述图像中,计算结果的值可能为正数,也可能为负数。所以,需要对计算结果取绝对值,以保证后续运算和显示都是正确的。
在 OpenCV 内使用函数 cv2.Laplacian()实现 Laplacian 算子的计算,该函数的语法格式为:
dst = cv2.Laplacian( src, ddepth[, ksize[, scale[, delta[, borderType]]]] )
式中:
- dst 代表目标图像。
- src 代表原始图像。
- ddepth 代表目标图像的深度。
- ksize 代表用于计算二阶导数的核尺寸大小。该值必须是正的奇数。
- scale 代表计算 Laplacian 值的缩放比例因子,该参数是可选的。默认情况下,该值为 1,表示不进行缩放。
- delta 代表加到目标图像上的可选值,默认为 0。
- borderType 代表边界样式。
该函数分别对 x、y 方向进行二次求导,具体为:
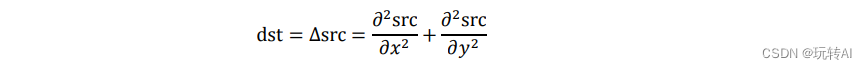
上式是当 ksize 的值大于 1 时的情况。当 ksize 的值为 1 时,Laplacian 算子计算时采用的 3×3的核如下:
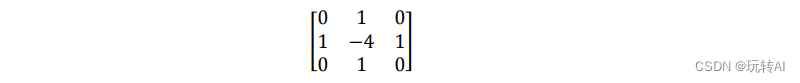
通过从图像内减去它的 Laplacian 图像,可以增强图像的对比度,此时其算子如图 9-27 所示。

代码示例:
使用函数 cv2.Laplacian()计算图像的边缘信息。
import cv2
o = cv2.imread('Laplacian.bmp',cv2.IMREAD_GRAYSCALE)
Laplacian = cv2.Laplacian(o,cv2.CV_64F)
Laplacian = cv2.convertScaleAbs(Laplacian)
cv2.imshow("original",o)
cv2.imshow("Laplacian",Laplacian)
cv2.waitKey()
cv2.destroyAllWindows()
运行结果:
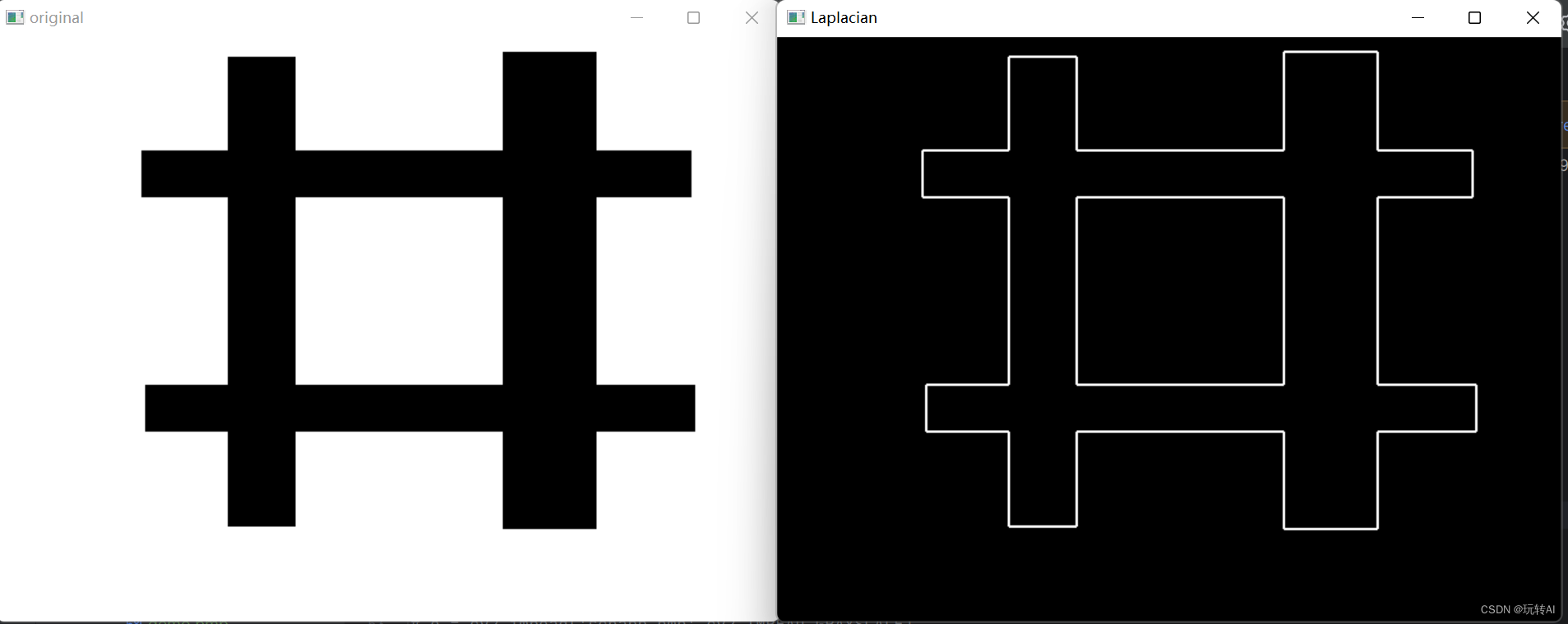
左图为原始图像,右图为得到的边缘信息。
算子总结
Sobel 算子、Scharr 算子、Laplacian 算子都可以用作边缘检测,它们的核如图 9-29 所示。
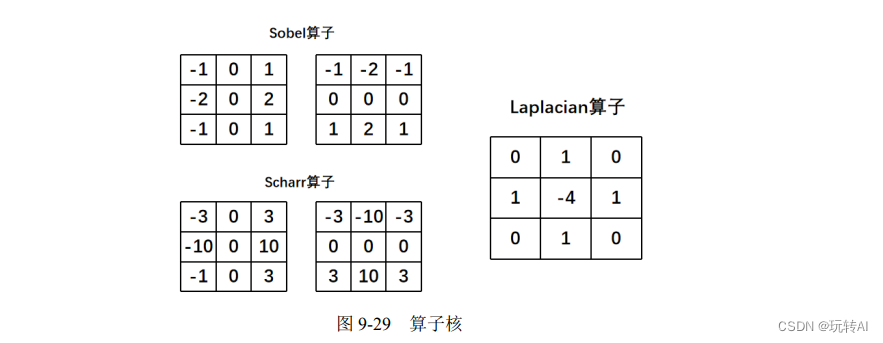
Sobel 算子和 Scharr 算子计算的都是一阶近似导数的值。通常情况下,可以将它们表示为:
Sobel 算子= |左-右| / |下-上|
Scharr 算子= |左-右| / |下-上|
式中“|左-右|”表示左侧像素值减右侧像素值的结果的绝对值,“|下-上|”表示下方像素值减上方像素值的结果的绝对值。像素值的结果的绝对值。
Laplacian 算子计算的是二阶近似导数值,可以将它表示为:
Laplacian 算子= |左-右| + |左-右| + |下-上| + |下-上|
通过公式可以发现,Sobel 算子和 Scharr 算子各计算了一次“|左-右|”和“|下-上|”的值,而 Laplacian 算子分别计算了两次“|左-右|”和“|下-上|”的值。