STSP中用于记录节点和旅行回路的四种数据结构
- 双链表结构
- 2-level tree
- 卫星结构
- k-level卫星结构树
- 参考文献
对于TSP是是历史悠久的研究问题,直至现在已经有了很多成熟高效的算法来求解问题。在拥有好的求解算法的同时,优秀的数据结构可以同时大幅提升问题的求解速率,简化问题的求解步骤,下面要介绍的就是关于对称TSP问题(STSP)的四种数据结构,四种结构层层递进,且看慢慢道来。(部分图片来自百度百科,部分图片来自参看文献)
双链表结构
双链表结构可能是简单应用比较多的数据结构

双链表的结构核心就在于每个节点有记录它的前驱结点和后继节点,我们分别用pre和suc表示,然后依次来链接起所有节点并组成完成的哈密顿回路。
在具有领先性的弹射算法如LKH中,嘴贱但2-opt move需要对链表进行反转,对于双链表结构,反转操作需要平均的O(n)复杂度进行pre和suc的互换,并且每次进行k-opt move的时候都需要进行O(n)的更新。由此,卫星结构就应运而生,在介绍卫星结构之前,再讲一下2-level tree。
2-level tree
2-leve tree在某种程度上解决了双链表结构反转部分旅行的操作的复杂性。下面我们先来看一下它的结构示意图。

两层树结构是讲部分结点视为一个segment,然后由一个上层结点记录对应的信息,比如上层结点记录自己麾下有几个结点,并记录段的开始和结尾等等。这就像公司里的分层次管理,员工有对应的leader带领。
在上面所述的翻转操作中,上层结点有一个reberse位,当发生翻转时就将那一位置1,这样遍历这一段的结点的时候就可以方向性地选择从那一边开始遍历。
上层结点同时也维护着上层结点之间的联系,有pre和suc等元素,反转操作只需要根据reverse位和O(n)级别地修改上层结点的指针指向即可。
但是问题在于,反转操作可能是跨越段之间的,所以这也是需要解决的一个难点所在。
卫星结构

上面是卫星结构和双链表的差别示意图
顾名思义,卫星结构是伴随的,也就是卫星结构是两个结点关联起来,同时又和其他结点进行连接,以组成类似双链表的循环结构,但一共有两个独立但又有连接的双层轨道。具体来说就是下面的这张图:
tour的序列是 2941638507
而每个结点在卫星结构中隔一个与下一个结点之间也建立联系
也即是,2连4,9连1,4连6,1连3,6连8,3连5,8连0,5连7,0连2,7连9
这样做的好处是,可以在常数O(1)内完成翻转操作,这也是卫星结构的精妙之处,也是它为什么可以作为论文发表的原因

下面是论文中给出的参考示意图
但是最关键的地方,确写的是obviously,在没有看源码的情况下,笔者花了一些时间去补上论文中跳过确实最关键的地方,这也是本篇blog的写作的主要目的和原因

笔者在这里用手推到一下
首先双轨循环结构是1234567的顺序的tour,根据卫星结构隔一个两两连接,以形成原始的黑色笔画出的结构。
当我们要进行2-5的翻转的时候,卫星结构按照蓝色笔所画的进行移动,注意这种移动看着是一个圈,但是在code中是常数级别且关键结点的修改即可。具体来说就是,上面的2-5和下面的4-7进行逆时针翻转。然后其他部分(上下部分)进行直接的替换(上换到下面,下面换到上面)之后的,按照原tour的方向的平移(musk掉逆转的那一部分),就可以得到双轨道都是进行部分翻转之后的结果。

k-level卫星结构树
而k-level tree的卫星结构树就是结合了卫星结构和2-level tree的优点
当然这也会使得数据结构变得更加复杂,毕竟简单和复杂,效率之间都是有一个权衡的。
下面是结构的示意图,因为是结合前面的各种优点的集合,这里就不再继续赘述了
在参考文献里有理论上的k的选择分析,还有之前数据结构的效率等等更加详细的分析
读者有兴趣可以去下载查看。需要指出的是,目前最常用的可能是2-level tree,至少在现有的弹射算法中,使用的通用结构是2-level tree。当然新的好的数据结构也值得我们去推广和使用。
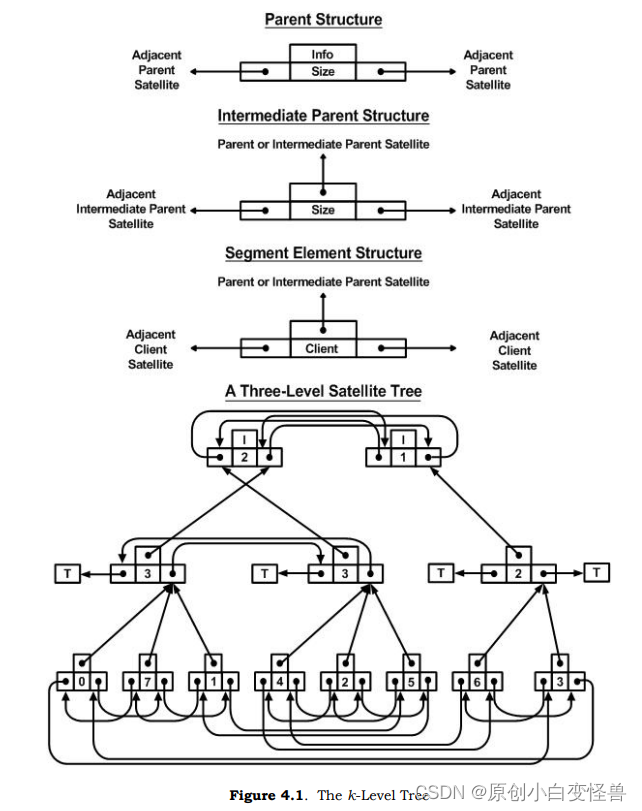
参考文献
The Satellite List and New Data Structures for Symmetric Traveling Salesman Problems