今天,我们将一起探索数字信号处理基础中至关重要的两个概念:连续信号离散化与采样定理。
一、为什么要做连续信号离散化?
在我们的日常生活中,信号无处不在。比如我们说话的声音、无线信号、图像信号等等,这些信号都是连续的。那么,为什么要对连续信号进行离散化呢?
连续信号是在时间和幅度上都连续变化的,无法直接被数字设备处理。所以,我们需要将连续信号转换为离散信号,这个过程就叫做连续信号离散化,也就是“采样”,实际就是用ADC转换器来采样。
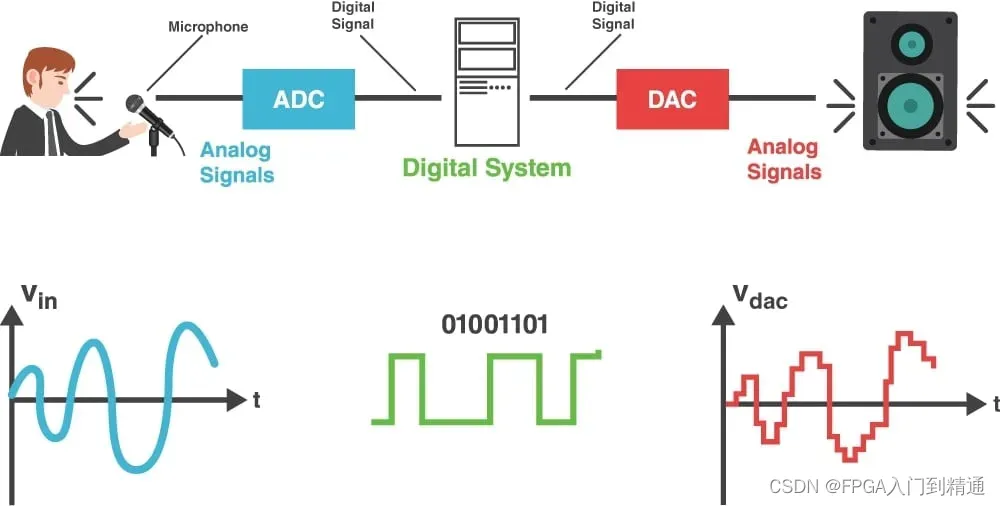
这样采集的离散数字信号,可以使用二进制数据表示,方便数字设备进行存储、处理、传输等操作啦。
二、什么是采样定理?
采样定理可是数字信号处理的核心基础,它提供了如何使模拟信号转换为数字信号而不失真的依据。
1、奈奎斯特定理
fs>2*fmax,其中fs是采样频率,fmax是被采样信号中的最高频率。
也就是说,如果要对一个带宽受限的连续信号进行采样而不引起失真,采样频率必须大于信号最高频率的两倍。
奈奎斯特定理主要适用于理想低通信道,即无噪声且带宽有限的情况。
极限数据传输率 = 2Wlog₂V,其中 W 是信道带宽,V 表示每个码元离散电平的数目。
它给出了无噪声信道中理论上的最大数据传输速率,对码元传输速率进行了限制,要提高数据传输速率可采用多元制调制方法。常被用于理论分析理想信道下的性能。
2、香农定理
香农定理适用于带宽受限且有高斯白噪声干扰的信道。
信道的极限数据传输速率 = Wlog₂(1 + S/N)。这里 W 为信道带宽,S 为信号平均功率,N 为噪声功率,S/N 是信噪比。
考虑了噪声的影响,得出在有噪声干扰情况下信道的极限数据传输速率,对现代通信系统的设计和优化有重要指导意义,可用于确定通信系统参数、选择调制解调方式和编码方案等。
3、采样的时域模型示例
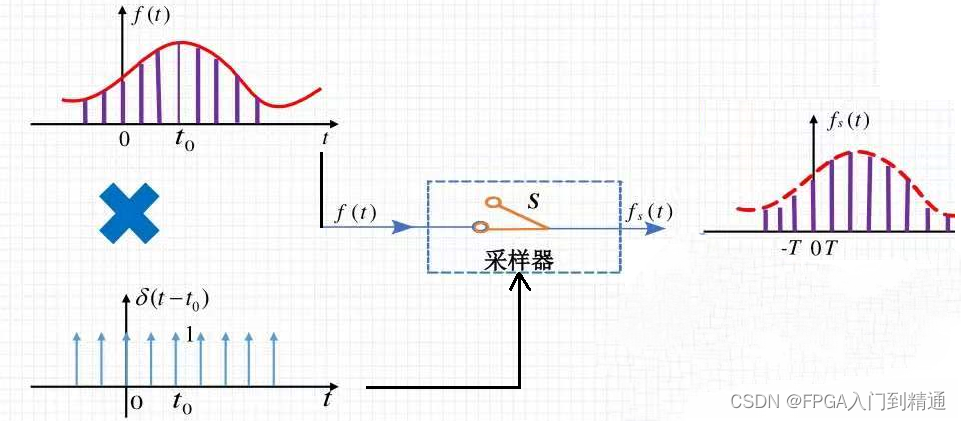
采样器可以看成脉冲式开关,通过周期性开关采样器,来获取时域连续信号的幅度。
当采样器闭合时,时域连续信号所包含的谐波频率分量都可以通过。
这里有两个关键参数:
(1)脉冲信号的持续时间τ,理想值无限趋近于0。
(2)脉冲信号的频率, 即采样频率fs。
采样频率对于采样信息结果的影响很大,采样频率太小,采样点数就很少,信号信息丢失就很大;
三、混叠现象
混叠是指在对连续时间信号进行取样以数字化时,由于取样频率低于两倍奈奎斯特频率,导致取样信号被还原成连续信号时产生彼此交叠而失真的现象。
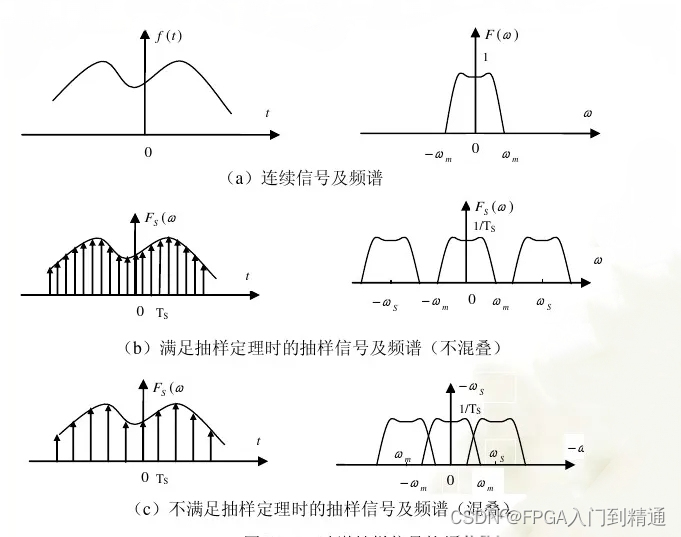
当混叠发生时,原始信号无法从取样信号还原。混叠可能发生在时域上,称作时间混叠,也可能发生在频域上,称作空间混叠。
为了避免混叠现象发生,可以采取提高采样频率(即缩小采样时间间隔),但实际的信号处理系统不可能达到很大的采样频率,且许多信号本身可能含有较高频率成分,不可能将采样频率提高到足够高;
另一种方法是采用抗混滤波器,在采样频率一定的前提下,通过低通滤波器滤掉高于奈奎斯特频率(fs/2)的频率成分,通过低通滤波的信号则可避免出现频率混叠。

如果需要更多学习资料和源码,想要学习FPGA实战入门进阶,请阅读下面这篇文章:
FPGA入门真的难吗?少走弯路,少踩坑。







