信息熵
比特化
等概率时花费的时间比较多
随机变量不是等概率出现的时候,bit更小,传输速率更快

在等概率情况下,具体是哪个意思比较难猜,每个可能都是等概率,很难猜中具体是哪个,信息量就很大
举个我自己理解的小栗子:
“你去刷碗” :很具体,就是就是刷碗这件事,信息熵就小
“你猜猜我想让你干什么?” :这就很模糊,信息量大,信息熵就大
信息熵就是用来描述系统信息量的不确定度
信息熵越小就越纯
条件熵

决策树
可以按照gini系数或者信息熵来做决策树
按照样本的每一列来构造一个树,然后通过这个树来决定和判断这个样本的类型
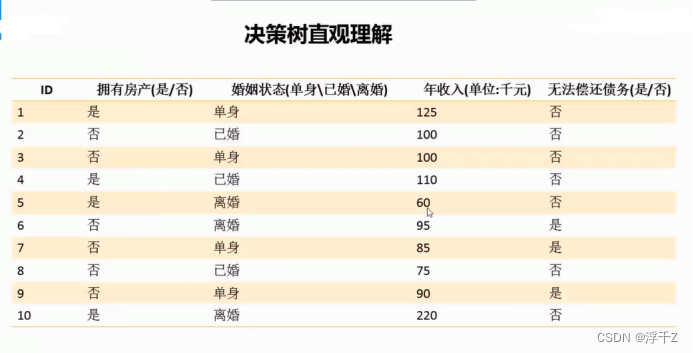
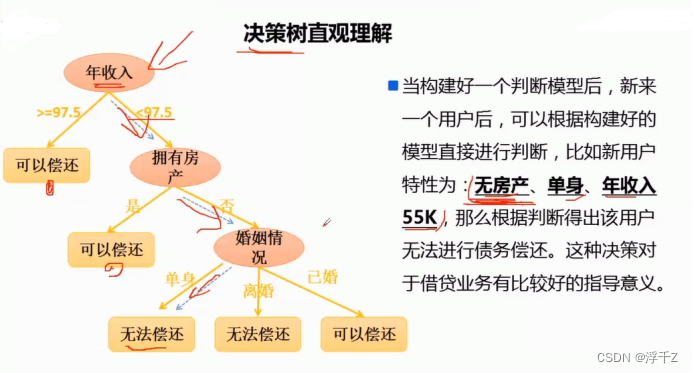
每个叶子结点都代表一个类别
决策树是一个有监督的分类算法
决策树分两大类,分类树和回归树
信息熵:熵值越小,越容易区分


决策树量化纯度

Gain越大,表示用这个条件分越纯,越合理

由上图可见,收入的信息增益Gain最大,先用收入来分
决策树生成算法
建立决策树的主要是以下三种算法
◆ID3
◆C4.5
CART ( Classification And Regression Tree )
ID3

C4.5


CART

分类示例
步骤
数据加载
数据处理(这里用了降维)
数据分割(分割成训练集和测试集)
创建并训练模型
模型评估
5.1 生成不同种类的样本数据
5.2 对数据进行预测
5.3 构建3中颜色map对象
5.4 显示3种背景
5.5 画训练集样本
5.6 画测试集样本
画ROC曲线
代码
#coding=UTF-8
import numpy as np
import pandas as pd
defaultencoding = 'utf-8'
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
#1.数据加载
datas=pd.read_csv("iris.data",header=None,sep=",")#加载数据
X=datas.iloc[:,0:-1]#取x
Y=datas.iloc[:,-1]#最后一列
Y=pd.Categorical(Y).codes#编码
# 在数据分析中,经常需要对分类数据进行编码,即将非数值型的数据转换为数值型的数据,以便进行数据分析和建模。Pandas库中提供了Categorical类型,可以方便地进行分类变量的转换和管理。
# 其中,pd.Categorical(Y).codes可以将分类变量Y转换为数值型变量,并返回一个由整数组成的数组。
# 其中,每个整数都对应于相应分类变量的唯一编码。
#
# 举个例子,如果我们有一个包含颜色信息的分类变量Y,其中包含了"red"、"green"和"blue"三种颜色,
# 我们可以使用pd.Categorical(Y).codes将其转换为对应的整数编码,
# 比如"red"对应的编码为0,"green"对应的编码为1,"blue"对应的编码为2。#2.数据处理 降维
#Laso 求出来theta为0
#主成分析:降维
from sklearn.decomposition import PCA#降维
# 通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中,实现数据特征的降维
pca=PCA(n_components=2)#n_components表示降成2个特征列
X=pca.fit_transform(X)#转换成2列
#3.数据分割
from sklearn.model_selection import train_test_split#训练集测试集分割
train_x,test_x,train_y,test_y=train_test_split(X,Y,test_size=0.2,random_state=2)
#4.创建模型并训练模型
from sklearn.tree import DecisionTreeClassifier#导入决策树分类
# DecisionTreeClassfier的参数有# 1.criterion gini or entropy# 2.splitter best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中(数据量大的时候)# 3.max_features 默认是None(所有),log2,sqrt,N 特征小于50的时候一般使用所有的# #N就是特征属性的个数# 4.max_depth 数据少或者特征少的时候可以不管这个值,如果模型样本量多,特征也多的情况下,可以尝试限制下# #防止过拟合# 5.min_samples_split 如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分。# 如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。# 6.min_samples_leaf 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被# 剪枝,如果样本量不大,不需要管这个值,大些如10W可是尝试下# 7.min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起# 被剪枝默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,# 或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。# 8.max_leaf_nodes 通过限制最大叶子节点数,可以防止过拟合,默认是"None”,即不限制最大的叶子节点数。# 如果加了限制,算法会建立在最大叶子节点数内最优的决策树。# 如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制# 具体的值可以通过交叉验证得到。# 9.class_weight 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多# 导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重# 如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。# 10.min_impurity_split 这个值限制了决策树的增长,如果某节点的不纯度# (基尼系数,信息增益,均方差,绝对差)小于这个阈值# 则该节点不再生成子节点。即为叶子节点 。
# best表示当前数据集是最优,但将来的数据集不一定最优,所以可选 random max_features最多选几个特征(列)
decision_tree=DecisionTreeClassifier(criterion="gini",splitter="random",max_features=2,random_state=2)#这里选择用gini系数来构建决策数
decision_tree.fit(train_x,train_y)#fit用来决策树构建
#预测
# test_y_hat=decision_tree.predict(test_x)#预测:分类:多数表决法,或加权多数表决法
#4.模型评估
score=decision_tree.score(test_x,test_y)#这个方法会返回该模型下的准确率
#求R^2 接近于1更好
# 4.1生成样本数据
# print proba
#得到第0列最大值 最小值
minx1=np.min( X[:,0])
maxx1=np.max( X[:,0])
#得到第1列最大值 最小值
minx2=np.min( X[:,1])
maxx2=np.max( X[:,1])
#
N=100
#根据原数据第0列,最大值,最小值成生100个数据
X1=np.linspace(minx1,maxx1,100)#生成X第一列最大值和最小值之间100个值
#根据原数据第1列最大值,最小值成生100个数据
X2=np.linspace(minx2,maxx2,100)#生成X第二列最大值和最小值之间100个值#生坐标点
X1,X2=np.meshgrid(X1,X2)
#合成2列数据 一万行数据(100*100)
grid_X=np.dstack((X1.ravel(),X2.ravel()))[0]#ravel把二维数组变成一维数组
# 4.2对一万数据进行预测
grid_hat=decision_tree.predict(grid_X) #预测#4.3构建3种颜色map对象
c=mpl.colors.ListedColormap(['aliceblue', 'antiquewhite', 'aqua'])#取pthon颜色前3个
plt.figure()
plt.subplot(2,1,1)#显示第一个子图
print("========================")
print(X1.shape,0000000)
#第三个参数是颜色
#4.4显示3种背景
plt.pcolormesh(X1,X2,grid_hat.reshape(X1.shape),cmap=c)#显示3块背景
# plt.pcolormesh(X1,X2,grid_hat.reshape(X1.shape),cmap=c)是一种用于可视化分类边界的方法,
# 其中X1和X2是两个特征的网格点坐标矩阵,grid_hat是分类器预测的结果,cmap是颜色映射方案。
# 这个函数将会把grid_hat的值根据颜色映射方案显示在网格坐标(X1,X2)对应的位置上,从而形成分类的背景。
#
# 更具体地说,plt.pcolormesh()函数的作用是对网格坐标中每个小矩形(由相邻的四个点围成)进行填充颜色,颜色的深浅取决于grid_hat预测结果的值。
# 因此,如果分类器能够很好地区分不同的类别,则可以看到3块不同颜色的背景。
#
# 需要注意的是,X1、X2和grid_hat都是二维数组,因此需要使用reshape()函数将grid_hat从一维数组变成和X1、X2相同的二维数组,以便正确绘制分类背景。# 4.5画原训练样本
plt.scatter(train_x[:,0],train_x[:,1],c=train_y)#显示训练集点
# 这是一个使用 matplotlib 库中的 scatter 方法进行绘图的例子。
# 其中 train_x[:,0] 和 train_x[:,1] 是训练集中所有样本的第一列和第二列特征,train_y 是训练集中所有样本的标签。
# scatter 方法将第一列特征作为 x 轴,第二列特征作为 y 轴,根据标签 train_y 对数据点进行颜色编码,最终显示出一个二维散点图,其中不同颜色的点代表不同的类别。
#
# 具体而言,plt.scatter(train_x[:,0],train_x[:,1],c=train_y) 中的参数 train_x[:,0] 表示取训练集中所有样本的第一列特征作为 x 轴数据;
# train_x[:,1] 表示取训练集中所有样本的第二列特征作为 y 轴数据;c=train_y 表示根据 train_y 中不同的标签对散点图上的数据点进行颜色编码。# 4.6画原测试集样本
plt.scatter(test_x[:,0],test_x[:,1],c=test_y)#显示测试集点
plt.title("决策树算法 准确率"+str(score))
#5.画ROC曲线
plt.subplot(2,1,2)#显示第二个子图
import sklearn.metrics as metrics
from sklearn.preprocessing import label_binarize
proba=decision_tree.predict_proba(test_x)#求概率
lbl=label_binarize(test_y,classes=(0,1,2))
fpr,tpr,tharehold=metrics.roc_curve(lbl.ravel(),proba.ravel())
plt.plot(fpr,tpr,c="red")#ROC
plt.title("AUC:"+str(metrics.auc(fpr,tpr)))
plt.show()结果
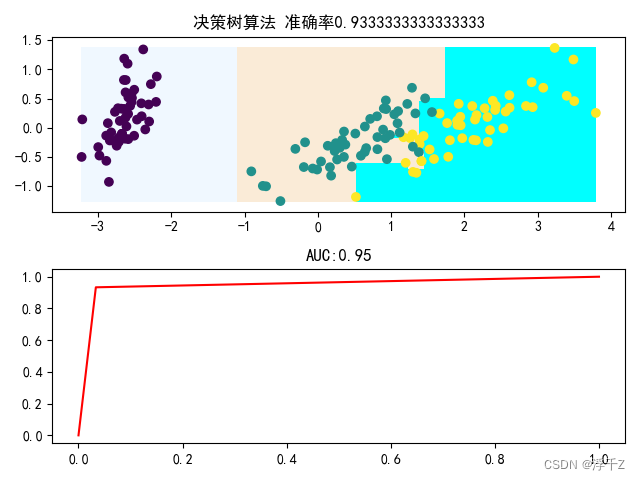
并不是列数越多越好,容易造成过拟合,得适中
Lasso回归里面,求出来theta为0,就是降维操作
这里用的是PCA降维
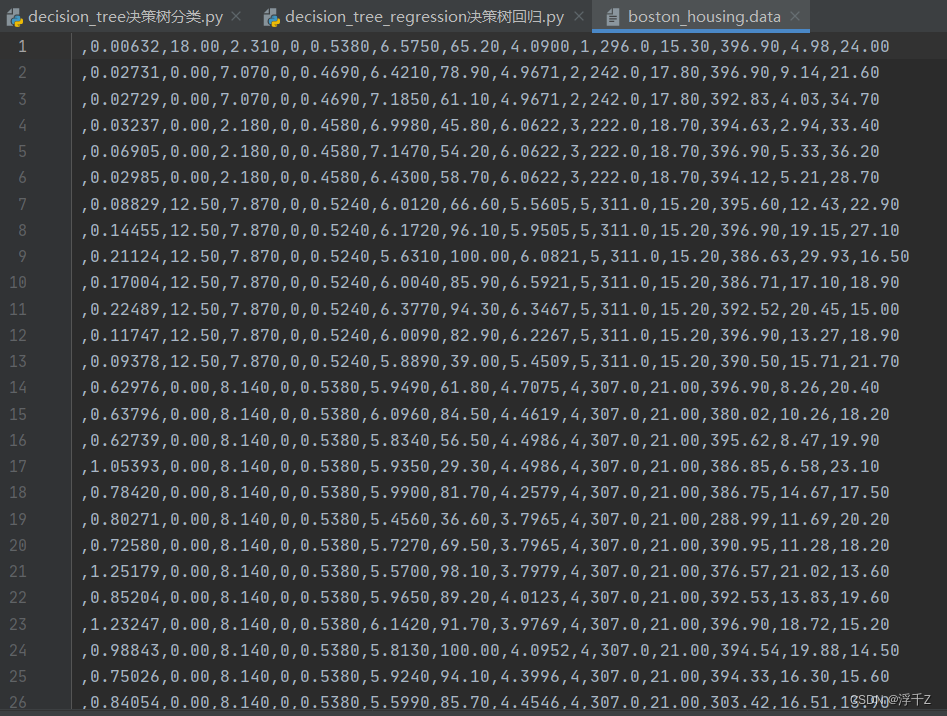
数据预览
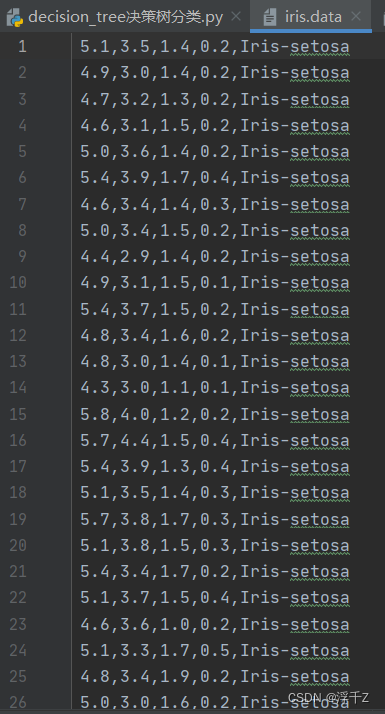
回归示例
代码
#coding=UTF-8
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression,RidgeCV,LassoCV
from sklearn.preprocessing import StandardScaler
import matplotlib as mpl
import sys
defaultencoding = 'utf-8'mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
# CRIM - per capita crime rate by town 城镇人均犯罪率
# ZN - proportion of residential land zoned for lots over 25,000 sq.ft.占地面积超过25000平方英尺的住宅用地比例。
# INDUS - proportion of non-retail business acres per town.每个城镇非零售商业用地的比例
# CHAS - Charles River dummy variable (1 if tract bounds river; 0 otherwise) Charles River虚拟变量(如果tract bounds river,则为1;否则为0)
# NOX - nitric oxides concentration (parts per 10 million)一氧化氮浓度(百万分之一)
# RM - average number of rooms per dwelling每个住宅的平均房间数
# AGE - proportion of owner-occupied units built prior to 19401940年以前建设的业主单位比例
# DIS - weighted distances to five Boston employment centres 到波士顿五个就业中心的加权距离
# RAD - index of accessibility to radial highways 放射状公路可达性指标
# TAX - full-value property-tax rate per $10,000 每10000美元的全额物业税税率
# PTRATIO - pupil-teacher ratio by town 城镇师生比
# B - 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town1000(bk-0.63)^2,其中bk是按城镇划分的黑人比例
# LSTAT - % lower status of the population 人口地位低下状态
datas=pd.read_csv("boston_housing.data",sep=",",header=None)
datas=datas.replace(np.NaN,0)
datas=datas.dropna(axis=1,how="any")
X=datas.iloc[:,1:-1]
Y=datas.iloc[:,-1]
# print Y
train_x,test_x,train_y,test_y=train_test_split(X,Y,test_size=0.2,random_state=2)
#决策树,训练、预测值、算分数
decisionTree=DecisionTreeRegressor(criterion="friedman_mse",splitter="random",min_samples_leaf=4)
decisionTree.fit(train_x,train_y)
decisionTree_y_hat=decisionTree.predict(test_x)
print(decisionTree.score(test_x,test_y))
#线性回归,训练、预测值、算分数
linear=LinearRegression()
linear.fit(train_x,train_y)
linear_y_hat=linear.predict(test_x)
# print linear.score(test_x,test_y)
#岭回归,训练、预测值、算分数
ridge=RidgeCV(alphas=np.logspace(-3,1,20),cv=2)
ridge.fit(train_x,train_y)
ridge_x_hat=ridge.predict(test_x)
ridge_score=ridge.score(test_x,test_y)
#lasso回归,训练、预测值、算分数
lasso=LassoCV(alphas=np.logspace(-3,1,20),cv=2)
lasso.fit(train_x,train_y)
lasso_x_hat=lasso.predict(test_x)
lasso_score=lasso.score(test_x,test_y)
#开始画图
plt.figure()
r=range(len(test_x))
import matplotlib.colors as colors
print(colors.cnames.keys())
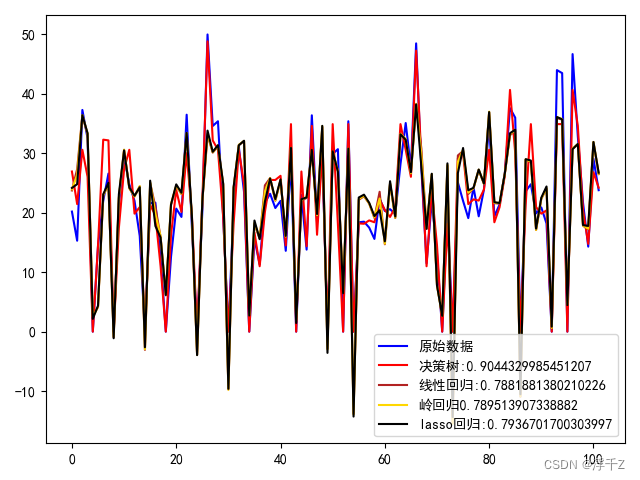
plt.plot(r,test_y,c="blue",label="原始数据")
plt.plot(r,decisionTree_y_hat,c="red",label="决策树:"+str(decisionTree.score(test_x,test_y)))
plt.plot(r,linear_y_hat,c="firebrick",label="线性回归:"+str(linear.score(test_x,test_y)))
plt.plot(r,ridge_x_hat,c="gold",label="岭回归"+str(ridge_score))
plt.plot(r,lasso_x_hat,c="black",label="lasso回归:"+str(lasso_score))
plt.legend()
plt.show()
结果
数据预览