1.基于BN层剪枝
基于Batch Normalization (BN)层进行剪枝是一种常用的模型压缩方法,特别是在卷积神经网络(CNNs)中。BN层在训练期间用于加速收敛和提高模型的泛化能力,而在剪枝过程中,BN层提供的统计信息(特别是均值(mean)和方差(variance))可以用来指导剪枝决策,帮助识别哪些特征图或通道的重要性较低,从而可以安全移除。下面是基于BN层剪枝的基本步骤和原理:
### 原理
1. **重要性评估**:BN层提供了每个通道的均值和方差,这些统计量可以反映通道的活跃程度。一般认为,具有较低方差的通道对模型的输出贡献较小,因为它们传递的信息变化不大,因此可以视为不太重要的特征。此外,还可以考虑使用BN层的γ(scale)参数,因为γ反映了该通道在标准化后被放大的程度,γ值接近于零的通道可以视为贡献较小。
2. **通道排序**:基于上述指标(通常是方差或γ值),对所有通道进行排序,以确定哪些通道是最不重要的。
3. **剪枝决策**:根据预设的剪枝比例(比如想要移除50%的通道),从排序列表的底部开始移除通道。实际操作中,可能会设置一个阈值,只有当γ值或方差低于该阈值的通道才会被剪除。
4. **微调**:剪枝后的模型需要重新训练(微调)以恢复因剪枝可能造成的性能损失。这个阶段模型会重新学习如何高效利用剩下的通道。
### 注意事项
- **剪枝策略**:除了基于BN层的统计信息外,还可以结合其他指标,如通道的绝对权重大小,或是基于输出的敏感度分析来辅助剪枝决策。
- **结构化剪枝**:确保剪枝操作保持网络结构的规则性,例如,整除的通道数利于在硬件上实现加速。
- **多次迭代**:剪枝和微调可能需要多次迭代进行,逐步减少通道数量直至达到理想的模型大小与性能平衡。
基于BN层的剪枝方法因其简单有效,成为了模型压缩领域中的一个标准技术,尤其适合于深度学习模型的轻量化和加速部署。
2.稀疏训练
稀疏训练模型是一种优化技术,旨在通过在训练过程中引入稀疏性来减少神经网络中的参数数量,进而提升模型的效率、减少内存占用和计算成本,同时保持或接近原始模型的预测能力。以下是稀疏训练模型的一些核心技术优势和特点:
1. **高效计算**:稀疏模型通过让大部分权重为零或近似零,可以利用稀疏矩阵运算技术大幅减少实际参与计算的参数数量,从而降低计算复杂度和所需资源。
2. **内存与存储节省**:由于大量参数为零,存储和传输模型时只需关注非零参数,这显著减小了模型的体积,降低了对内存和硬盘空间的需求。
3. **加速硬件执行**:现代硬件加速器(如GPU和TPU)能够高效处理稀疏数据结构,通过跳过零值计算,加快了模型推理速度。
4. **负载均衡**:在诸如稀疏专家混合模型(SMoE)中,通过智能的门控机制实现专家间的负载均衡,确保计算资源的有效利用,避免计算瓶颈。
5. **模型性能提升**:通过集中利用少数关键参数,稀疏模型有时能在特定任务上达到或超越密集模型的性能,尤其是在处理高维度数据和大规模模型时。
6. **特征选择与可解释性**:稀疏性促进了特征选择,使得模型更容易解释,因为非零权重对应了对预测贡献显著的特征。
7. **训练与优化策略**:稀疏训练涉及特定的训练和优化策略,如使用稀疏正则化(如L1、L0正则化)、动态剪枝、稀疏激活函数等,以在训练过程中逐步诱导模型趋向稀疏。
8. **结构化稀疏性**:在某些情况下,稀疏性被设计成有结构的形式(如整个通道或滤波器的移除),这有利于硬件加速并保持模型结构的完整性。
综上所述,稀疏训练模型是一种重要的机器学习优化技术,它通过减少模型的冗余,提高了模型的效率和实用性,同时在很多情况下保持了模型的预测性能。随着计算硬件对稀疏计算支持的不断优化,稀疏训练模型的应用前景愈发广泛。
3.权重衰减
模型训练中的权重衰减(Weight Decay)是一种常用的正则化技术,旨在减少模型过拟合的风险,提升模型的泛化能力。它通过在损失函数中加入一个惩罚项来实现,这个惩罚项与模型参数(权重)的平方和成正比。权重衰减的数学表达式通常被整合进梯度下降或其他优化算法中,形式上等同于L2正则化。
### 基本原理
权重衰减的工作原理是通过向损失函数添加一个与模型参数的平方和成正比的惩罚项,促使学习算法在最小化经验误差的同时,也倾向于学习到权重较小的模型。具体来说,假设原始的损失函数为\(L(\theta)\),其中\(\theta\)代表模型的所有参数,权重衰减项(L2正则化)可以表示为\(\lambda \sum_{i} \theta_i^2\),其中\(\lambda\)是超参数,控制正则化的强度。因此,带权重衰减的损失函数变为:
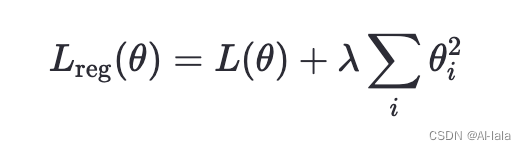
### 效果
1. **防止过拟合**:通过限制权重的大小,权重衰减有助于避免模型过度依赖训练数据中的噪声或偶然特性,从而提高模型在未见数据上的表现。
2. **促进权重稀疏**:虽然L1正则化更直接地促进稀疏解,但较大的L2正则化系数也可能导致某些权重趋近于零,间接实现一定程度的稀疏性。
3. **提高泛化能力**:通过减少模型复杂度,权重衰减有助于模型学习到更一般性的数据规律,提升泛化性能。
4. **数值稳定性**:权重衰减还有助于提高训练过程的数值稳定性,因为它可以防止权重值在迭代过程中变得过大。
### 实现
在实践中,权重衰减经常直接内置在优化算法中,例如,在使用Adam、SGD等优化器时,可以直接设置weight_decay参数来启用权重衰减功能。需要注意的是,不同库或框架在实现时可能对\(\lambda\)的定义稍有不同,有些会将其乘以0.5以便与L2范数的数学定义相匹配。
总之,权重衰减是一种简单而有效的正则化技术,通过增加对模型复杂度的惩罚,帮助模型在学习数据特征的同时,保持一定的泛化能力。