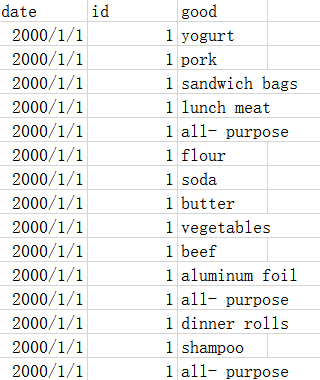第2关：动手实现Apriori算法

任务描述

本关任务：编写 Python 代码实现 Apriori 算法。

相关知识

为了完成本关任务，你需要掌握 Apriori 算法流程。

Apriori 算法流程

Apriori 算法的两个输人参数分别是最小支持度和数据集。该算法首先会生成所有单个物品的项集列表。接着扫描交易记录来查看哪些项集满足最小支持度要求，那些不满足最小支持度的集合会被去掉。然后，对剩下来的集合进行组合以生成包含两个元素的项集。接下来，再重新扫描交易记录，去掉不满足最小支持度的项集。该过程重复进行直到所有项集都被去掉。

所以 Apriori 算法的伪代码如下：

1. while 集合中的项的个数 > 0:
2. 构建一个由 k 个项组成的候选项集的列表
3. 确认每个项集都是频繁的
4. 保留频繁项集并构建 k+1 项组成的候选项集的列表

从整个算法的流程来看，首先需要实现一个能够构建只有一个项集的函数，代码如下：

1. # 构建只有一个元素的项集， 假设dataSet为[[1, 2], [0, 1]. [3, 4]]
2. # 那么该项集为frozenset({0}), frozenset({1}), frozenset({2}),frozenset({3}), frozenset({4})
3. def createC1(dataset):
4. C1 = set()
5. for t in dataset:
6. for item in t:
7. item_set = frozenset([item])
8. C1.add(item_set)
9. return C1

有了从无到有之后，接下来需要从 1 到 K 。不过需要注意的是，这个时候需要排除掉支持度小于最小支持度的项集。代码实现如下：

1. # 从只有k个元素的项集，生成有k+1个元素的频繁项集，排除掉支持度小于最小支持度的项集
2. # D为数据集，ck为createC1的输出，minsupport为最小支持度
3. def scanD(D, ck, minsupport):
4. ssCnt = {}
5. for tid in D:
6. for can in ck:
7. if can.issubset(tid):
8. if can not in ssCnt.keys():
9. ssCnt[can] = 1
10. else:
11. ssCnt[can] += 1
12. numItems = len(D)
13. reList = []
14. supportData = {}
15. for key in ssCnt:
16. support = ssCnt[key]/numItems
17. if support >= minsupport:
18. reList.insert(0, key)
19. supportData[key] = support
20. #reList为有k+1个元素的频繁项集，supportData为频繁项集对应的支持度
21. return reList, supportData

这就完了吗？还没有！我们还需要一个能够实现构建含有 K 个元素的频繁项集的函数。实现代码如下：

1. #构建含有k个元素的频繁项集
2. #如输入为{0},{1},{2}会生成{0,1},{0, 2},{1,2}
3. def aprioriGen(Lk, k):
4. retList = []
5. lenLk = len(Lk)
6. for i in range(lenLk):
7. for j in range(i+1, lenLk):
8. L1 = list(Lk[i])[k:-2]
9. L2 = list(Lk[j])[:k-2]
10. if L1 == L2:
11. retList.append(Lk[i] | Lk[j])
12. return retList

有了这些小功能后，我们就能根据 Apriori 算法的流程来实现 Apriori 算法了。

编程要求

根据提示，在右侧编辑器 Begin-End 补充代码，实现 Apriori 算法。

测试说明

平台会对你编写的代码进行测试，若与预期输出一致，则算通关。

def createC1(dataset):C1 = set()for t in dataset:for item in t:item_set = frozenset([item])C1.add(item_set)return C1def scanD(D, ck, minsupport):ssCnt = {}for tid in D:for can in ck:if can.issubset(tid):if can not in ssCnt.keys():ssCnt[can] = 1else:ssCnt[can] += 1numItems = len(D)reList = []supportData = {}for key in ssCnt:support = ssCnt[key]/numItemsif support >= minsupport:reList.insert(0, key)supportData[key] = supportreturn reList, supportDatadef aprioriGen(Lk, k):retList = []lenLk = len(Lk)for i in range(lenLk):for j in range(i+1, lenLk):L1 = list(Lk[i])[k:-2]L2 = list(Lk[j])[:k-2]if L1 == L2:retList.append(Lk[i] | Lk[j])return retListdef apriori(dataSet,minSupport):# 首先找出最开始的数据项集C1 = createC1(dataSet)D = list(map(set,dataSet))# 把只有一个项集的支持率算出来L1,supportData = scanD(D,C1,minSupport)L = [L1]# 设置关联数k = 2while(len(L[k - 2]) > 0):# 然后开始循环找Ck = aprioriGen(L[k - 2], k)Lk, supK = scanD(D,Ck,minSupport)supportData.update(supK)L.append(Lk)k += 1return L,supportData

第3关：从频繁项集中挖掘关联规则

任务描述

本关任务：编写 Python 代码，实现挖掘关联规则的功能。

相关知识

为了完成本关任务，你需要掌握：关联规则挖掘算法流程。

从频繁项集中挖掘关联规则

要找到关联规则，需要从一个频繁项集开始。我们知道集合中的元素是不重复的，但我们想知道基于这些元素能否获得其他内容。例如某个元素或者某个元素集合可能会推导出另一个元素 。从小卖铺的例子可以得到，如果有一个频繁项集{薯片，西瓜}，那么就可能有一条关联规则薯片->西瓜。这意味着如果有人购买了薯片，那么在统计上他会购买西瓜的概率较大。

但是，这一条反过来并不总是成立。也就是说，即使薯片->西瓜统计上显著，那么薯片->西瓜也不一定成立。(从逻辑研究上来讲，箭头左边的集合称作前件，箭头右边的集合称为后件。)

那么怎样挖掘关联规则呢？在发现频繁项集时我们发现的是高于最小支持度的频繁项集，对于关联规则，也是用这种类似的方法。以小卖铺的例子为例，从项集{0, 1, 2, 3}产生的关联规则中，找出可信度高于最小可信度的关联规则。(PS:Apriori 原理对于关联规则同样适用。)

所以，想要根据上一关发现的频繁项集中找出关联规则，需要排除可信度比较小的关联规则，所以首先需要实现计算关联规则的可信度的功能。代码实现如下：

1. # 计算关联规则的可信度，并排除可信度小于最小可信度的关联规则
2. # freqSet为频繁项集，H为规则右边可能出现的元素的集合，supportData为频繁项集的支持度，brl为存放关联规则的列表，minConf为最小可信度
3. def calcConf(freqSet, H, supportData, brl, minConf = 0.7):
4. prunedH = []
5. for conseq in H:
6. conf = supportData[freqSet]/supportData[freqSet - conseq]
7. if conf >= minConf:
8. brl.append((freqSet - conseq, conseq, conf))
9. prunedH.append(conseq)
10. return prunedH

接下来就需要实现从频繁项集中生成关联规则的功能了，实现如下：

1. # 从频繁项集中生成关联规则
2. # freqSet为频繁项集，H为规则右边可能出现的元素的集合，supportData为频繁项集的支持度，brl为存放关联规则的列表，minConf为最小可信度
3. def ruleFromConseq(freqSet, H, supportData, brl, minConf = 0.7):
4. m = len(H[0])
5. if len(freqSet) > m+1:
6. Hmp1 = aprioriGen(H, m+1)
7. Hmp1 = calcConf(freqSet, Hmp1, supporData, brl, minConf)
8. if len(Hmp1) > 1:
9. ruleFromConseq(freqSet, Hmp1, supportData, brl, minConf)

编程要求

根据提示，在右侧编辑器 Begin-End 补充代码，将所有知识全部串联起来，实现关联规则生成功能。

测试说明

平台会对你编写的代码进行测试，若与预期输出一致，则算通关

代码：

from utils import apriori, aprioriGendef calcConf(freqSet, H, supportData, brl, minConf = 0.7):prunedH = []for conseq in H:conf = supportData[freqSet]/supportData[freqSet - conseq]if conf >= minConf:brl.append((freqSet - conseq, conseq, conf))prunedH.append(conseq)return prunedHdef ruleFromConseq(freqSet, H, supportData, brl, minConf = 0.7):m = len(H[0])if len(freqSet) > m+1:Hmp1 = aprioriGen(H, m+1)Hmp1 = calcConf(freqSet, Hmp1, supporData, brl, minConf)if len(Hmp1) > 1:ruleFromConseq(freqSet, Hmp1, supportData, brl, minConf)def generateRules(dataset, minsupport, minConf):'''生成关联规则，可以使用apriori函数获得数据集中的频繁项集列表与支持度:param dataset:数据集，类型为list:param minsupport:最小支持度，类型为float:param minConf:最小可信度，类型为float:return:关联规则列表，类型为list'''digRuleList = []L, supportData = apriori(dataset, minsupport)for i in range(1, len(L)):# freqSet为含有i个元素的频繁项集for freqSet in L[i]:H1 = [frozenset([item]) for item in freqSet]if i > 1:# H1为关联规则右边的元素的集合ruleFromConseq(freqSet, H1, supportData, digRuleList, minConf)else:calcConf(freqSet, H1, supportData, digRuleList, minConf)return digRuleList

第4关：超市购物清单关联规则分析

任务描述

本关任务：编写 Python 代码，挖掘出超市购物清单中潜在的关联规则。

相关知识

为了完成本关任务，你需要掌握：将知识运用到实际数据中。

超市购物清单关联规则分析

这里有一份超市的购物清单数据，数据的特征只有 3 个，分别为：交易时间，交易 id 和商品名称。如下图所示：

可以看出，在挖掘关联规则之前，我们需要整理一下数据，即根据交易 id 来将商品信息聚合起来，将数据变成我们关联规则分析算法所需要的形式。

当数据处理好之后，我们就可以使用之前编写的代码，来挖掘该数据的关联规则了。

编程要求

根据提示，在右侧编辑器 Begin-End 处补充代码，实现超市购物清单数据的关联规则挖掘功能。要求如下：

1.将所有商品名称转换为数字，转换关系如下：

1. {'yogurt':1, 'pork':2, 'sandwich bags':3, 'lunch meat':4, 'all- purpose':5, 'flour':6, 'soda':7, 'butter':8, 'vegetables':9, 'beef':10, 'aluminum foil':11, 'dinner rolls':12, 'shampoo':13, 'mixes':14, 'soap':15, 'laundry detergent':16, 'ice cream':17, 'toilet paper':18, 'hand soap':19, 'waffles':20, 'cheeses':21, 'milk':22, 'dishwashing liquid/detergent':23, 'individual meals':24, 'cereals':25, 'tortillas':26, 'spaghetti sauce':27, 'ketchup':28, 'sandwich loaves':29, 'poultry':30, 'bagels':31, 'eggs':32, 'juice':33, 'pasta':34, 'paper towels':35, 'coffee/tea':36, 'fruits':37, 'sugar':38}

2.关联规则列表中的商品必须是转换后的数字。

注意：数据文件为.csv文件，字段名分别为:date，id，good。

测试说明

平台会对你编写的代码进行测试，判题程序将自动将数字转换为商品名称：

测试输入：{'min_support':0.2,'min_conf':0.7} 预期输出：

1. eggs->vegetables:0.8378378378378379
2. juice->vegetables:0.780885780885781
3. cereals->vegetables:0.7849223946784922
4. individual meals->vegetables:0.7593457943925235
5. laundry detergent->vegetables:0.8167053364269142
6. butter->vegetables:0.7708830548926013
7. ice cream->vegetables:0.7599118942731278
8. yogurt->vegetables:0.8310502283105023                             

代码：

from utils import generateRules
import pandas as pddef T(x):m = {'yogurt': 1, 'pork': 2, 'sandwich bags': 3, 'lunch meat': 4, 'all- purpose': 5, 'flour': 6, 'soda': 7, 'butter': 8,'vegetables': 9, 'beef': 10, 'aluminum foil': 11, 'dinner rolls': 12, 'shampoo': 13, 'mixes': 14, 'soap': 15,'laundry detergent': 16, 'ice cream': 17, 'toilet paper': 18, 'hand soap': 19, 'waffles': 20, 'cheeses': 21,'milk': 22, 'dishwashing liquid/detergent': 23, 'individual meals': 24, 'cereals': 25, 'tortillas': 26,'spaghetti sauce': 27, 'ketchup': 28, 'sandwich loaves': 29, 'poultry': 30, 'bagels': 31, 'eggs': 32, 'juice': 33,'pasta': 34, 'paper towels': 35, 'coffee/tea': 36, 'fruits': 37, 'sugar': 38}return m[x]def aprior_data(data):basket = []for id in data['id'].unique():a = [data['good'][i] for i, j in enumerate(data['id']) if j == id]basket.append(a)return basketdef genRules(data_path, min_support, min_conf):# *********Begin*********#data1 = pd.read_csv(data_path)data1['good'] = data1['good'].apply(T)data2 = aprior_data(data1)rult = generateRules(data2, min_support, min_conf)return rult
#*********End*********#