目录
- 缺省参数
- 缺省参数概念
- 缺省参数分类
- 全缺省参数
- 半缺省参数
- 声明与定义分离
- 缺省参数的应用
- 函数重载
- 函数重载概念
- 例子1 参数类型不同
- 例子2 参数的个数不同
- 例子3 参数的顺序不同
- C++支持函数重载的原理--名字修饰(name Mangling)
感谢各位大佬对我的支持,如果我的文章对你有用,欢迎点击以下链接
🐒🐒🐒 个人主页
🥸🥸🥸 C语言
🐿️🐿️🐿️ C语言例题
🐣🐣🐣 python
🐓🐓🐓 数据结构C语言
🐔🐔🐔 C++
🐿️🐿️🐿️ 文章链接目录
缺省参数
缺省参数概念
缺省参数是声明或定义函数时为函数的参数指定一个缺省值。在调用该函数时,如果没有指定实参则采用该形参的缺省值,否则使用指定的实参
voivoid Func(int a = 0)
{cout << a << endl;
}
int main()
{Func();Func(10);return 0;
}
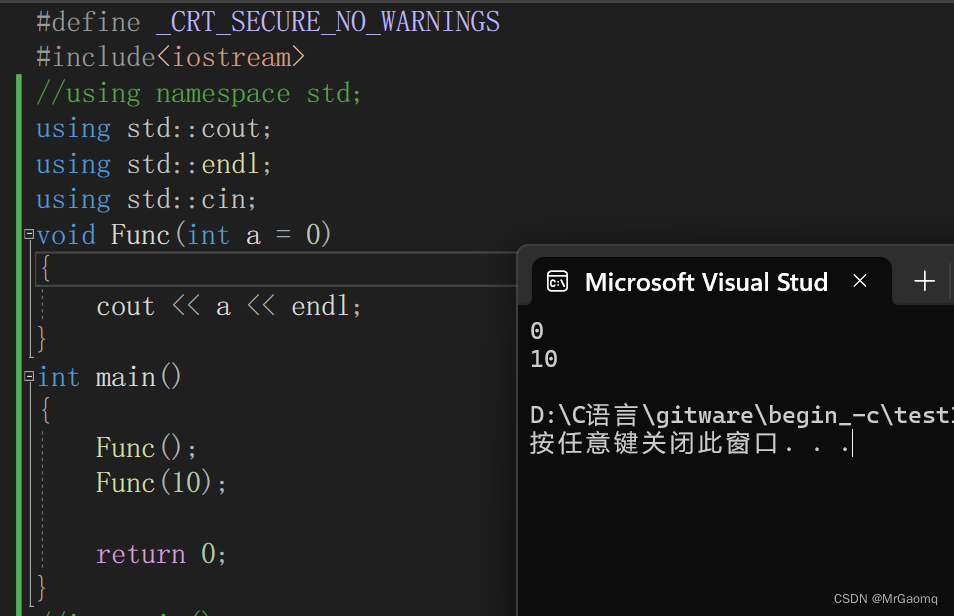
Func括号中的int a=0就是函数的缺省值
当我们在调用函数的时候,如果没有传入参数,那么就会让a=0作为我们传入的参数
当我们调用函数时,传入了参数10,那么传入的参数a就不等于0,而是等于10
许多函数传入的参数不止一个,缺省参数也是一样的
缺省参数分类
全缺省参数
void Func(int a = 10, int b = 20, int c = 30){cout<<"a = "<<a<<endl;cout<<"b = "<<b<<endl;cout<<"c = "<<c<<endl;}
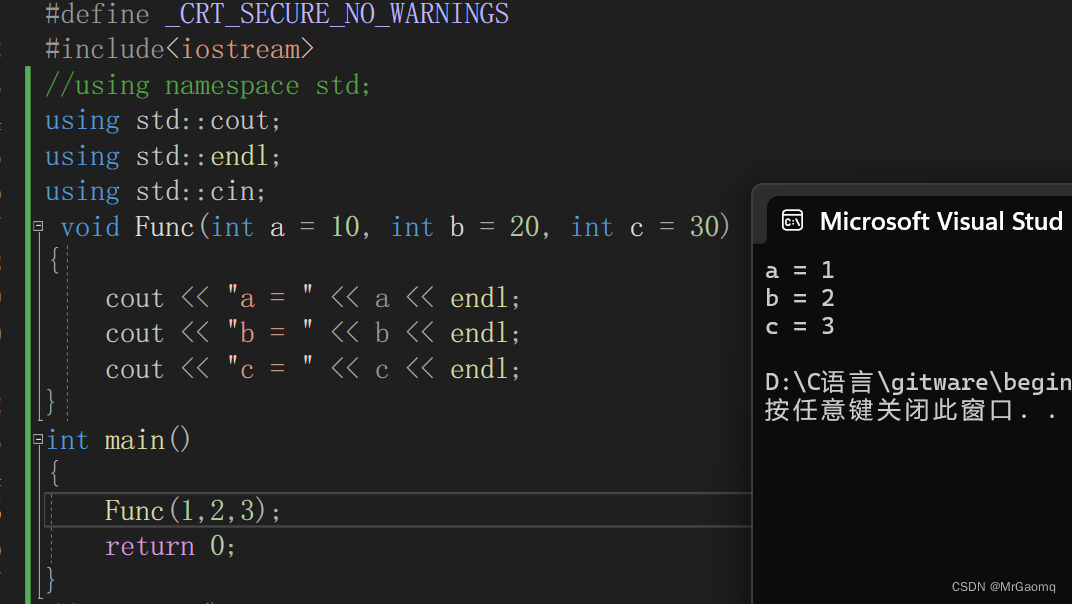
当只传两个参数时,打印的结果为
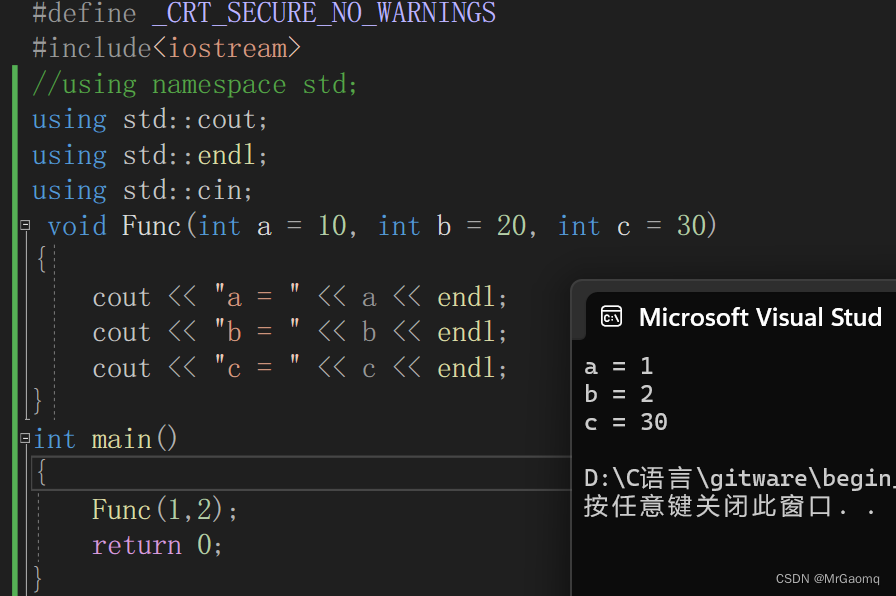
显然传入参数的顺序是从左往右依次开始传的
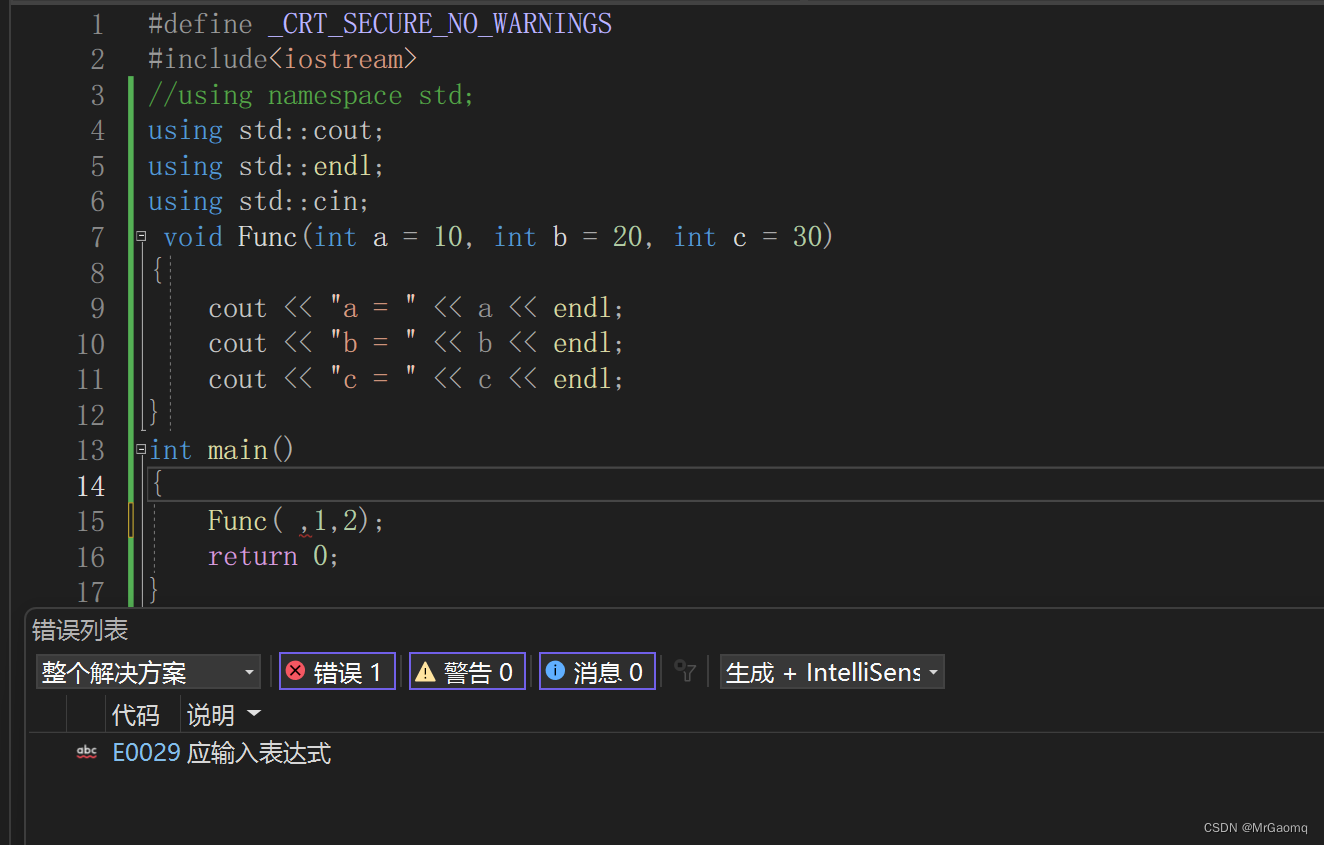
有的人想用Func(,1,2)这种方法去表示1为传给b的参数,2为传给c的参数,事实上这样是不行的
半缺省参数
void Func(int a, int b = 10, int c = 20){cout<<"a = "<<a<<endl;cout<<"b = "<<b<<endl;cout<<"c = "<<c<<endl;}
注意:
1. 半缺省参数必须从右往左依次来给出,不能间隔着给
2. 缺省参数不能在函数声明和定义中同时出现
3. 半缺省是缺省部分参数
声明与定义分离
//.h文件
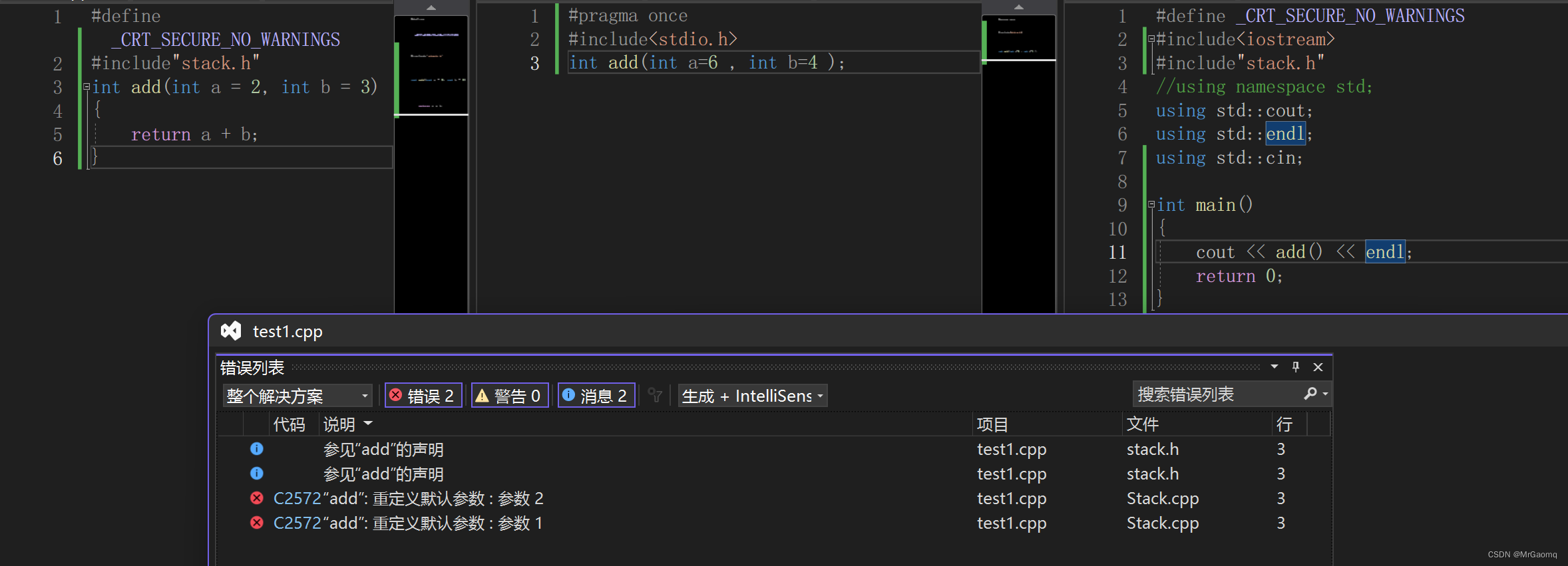
int add(int a = 6, int b = 4);// .cpp文件
int add(int a = 2, int b = 3)
{return a + b;
}
代码运行后会报错,重复默认参数,因为a和b在.h文件和.cpp文件中的缺省参数值不同起了冲突
如果.h文件和.cpp文件缺省参数值都相同时
//.h文件
int add(int a = 6, int b = 4);// .cpp文件
int add(int a = 6, int b = 4)
{return a + b;
}

那如果.h文件中我们不用缺省参数,而.cpp用缺省参数会怎么样
.h文件
int add(int a , int b );
.cpp文件
int add(int a=2 , int b=3 )
{return a + b;
}

这次只让.h文件用缺省参数
.h文件
int add(int a=6 , int b=4 );
.cpp文件
int add(int a , int b)
{return a + b;
}
综上声明和定义分离时缺省参数只能在声明给(.h文件),因为在test.cpp文件中要包含#include< xxx.h>文件,而包含了头文件后,编译器在预处理阶段会将头文件内容展开(把头文件的代码拷贝过来)
就相当于下面这段代码
int add(int a = 6, int b = 4);
int main()
{cout << add() << endl;return 0;
}
但是由于只有一个函数的声明,我们还需要找到函数的地址(函数具体实现的地方),想要找到函数实现的地址,就要了解编译器的几个阶段:预处理->编译->汇编->链接,
预处理是将头文件展开,宏替换(#define),条件编译(if…),去掉注释
编译是检查语法,然后生成汇编代码
汇编将汇编代码转换成二进制的机器码
在链接的时候会将包含的头文件和test.cpp等等文件合并到一起,然后根据函数的名称去帮你找到具体实现函数的地址
所以在最后链接的时候,会帮你找到函数的地址,如果找不到就会报错
补充:缺省参数的缺省值必须是常量或者全局变量,C语言不支持确实参数(编译器不支持)
缺省参数的应用
下面是之前我们写栈的代码,因为这个栈是数组实现的,在扩容的时候比较麻烦,并且经常会消耗空间
typedef struct stack//数组栈
{int* a;int top;//栈顶int capacity;空间
}ST;
void STInit(ST* pst)//栈的初始化
{assert(pst);pst->a = NULL;pst->capacity = 0;pst->top = 0//或者pst->top = -1;
}
void STPush(ST* pst, STDataType x)//栈的插入和扩容
{assert(pst);if (pst->top == pst->capacity){int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;STDataType* tmp = realloc(pst->a, sizeof(STDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}pst->a = tmp;pst->capacity = newcapacity;}pst->a[pst->top] = x;pst->top++;
}
假设这个栈需要插入100个数据,根据上面的代码,扩容的过程如下
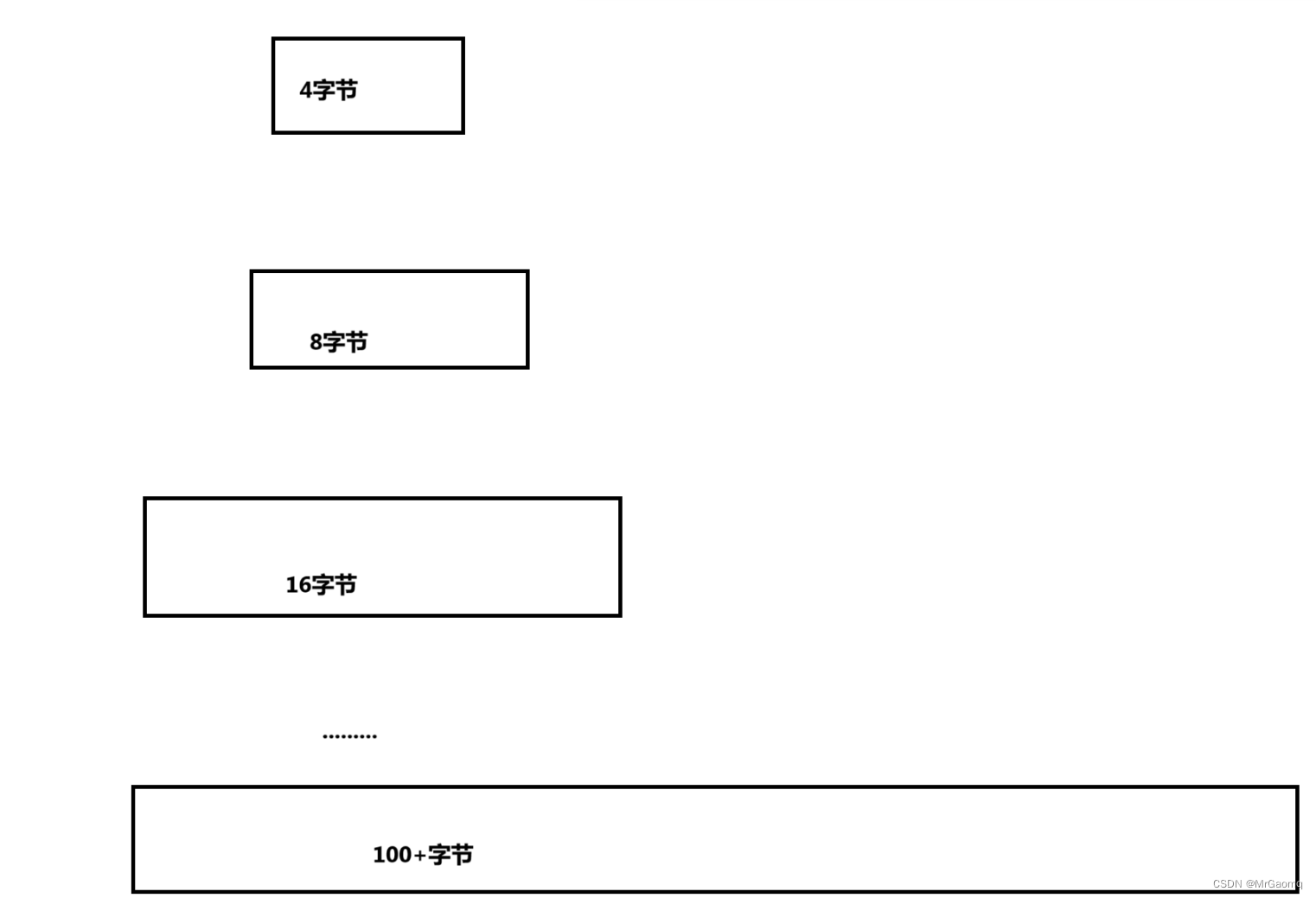
产生这个情况的原因就是因为这句代码STDataType* tmp = realloc(pst->a, sizeof(STDataType) * newcapacity),因为sizeof(STDataType) * newcapacity把扩容给写死了,每次扩容都是二倍的方式去括,而且有时扩容后的空间非常大,我们并不需要那么大的空间,就导致空间浪费
而有了缺省参数这个方法后,扩容的问题就得到了解决
我们只需要在栈的插入函数中加入缺省参数n=4
当栈为空时,就直接让栈扩容
当我们想要插入100个数据的时候,就给n传100
而当我们不知道要插入多少个数据的时候,就不给n传值,虽然可能会有空间浪费,但是问题不大
void STPush(ST* pst, STDataType x,int n=4)//栈的插入和扩容
{assert(pst);if (pst->top == pst->capacity){int newcapacity == n;STDataType* tmp = realloc(pst->a, sizeof(STDataType) * n);if (tmp == NULL){perror("realloc fail");return;}pst->a = tmp;pst->capacity = newcapacity;}pst->a[pst->top] = x;pst->top++;
}
函数重载
自然语言中,一个词可以有多重含义,人们可以通过上下文来判断该词真实的含义,即该词被重载了
函数重载概念
函数重载:是函数的一种特殊情况,C++允许在同一作用域中声明几个功能类似的同名函数
这些同名函数的形参列表(参数个数 或 类型 或 类型顺序)不同,常用来处理实现功能类似数据类型不同的问题
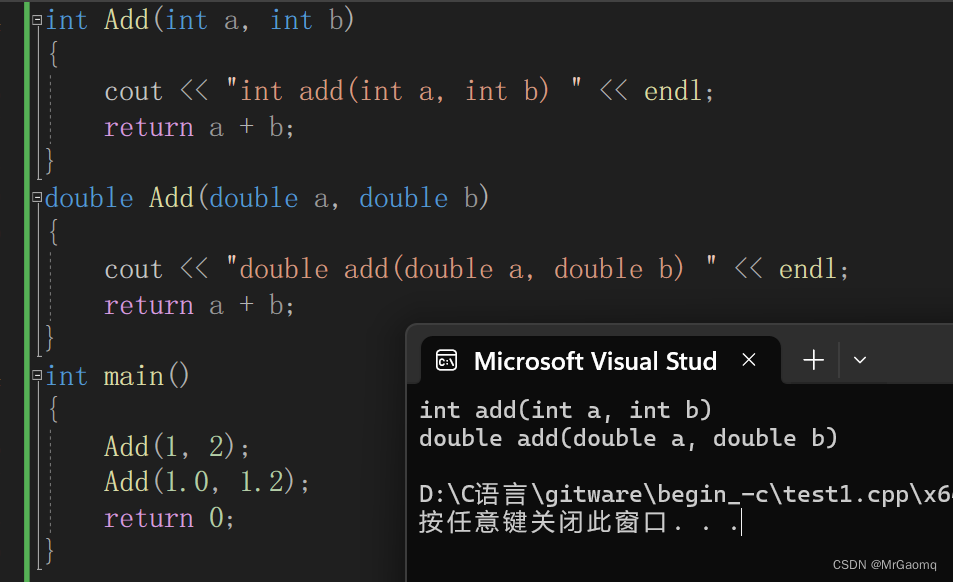
例子1 参数类型不同
int Add(int a, int b)
{cout << "int add(int a, int b) " << endl;return a + b;
}
double Add(double a, double b)
{cout << "double add(double a, double b) " << endl;return a + b;
}
int main()
{Add(1, 2);Add(1.0, 1.2);return 0;
}
例子2 参数的个数不同
int Add(int a, int b)
{cout << "int add(int a, int b) " << endl;return a + b;
}
int Add(int a)
{cout << "int add(int a) " << endl;return a ;
}
int main()
{Add(1, 2);Add(1);return 0;
}

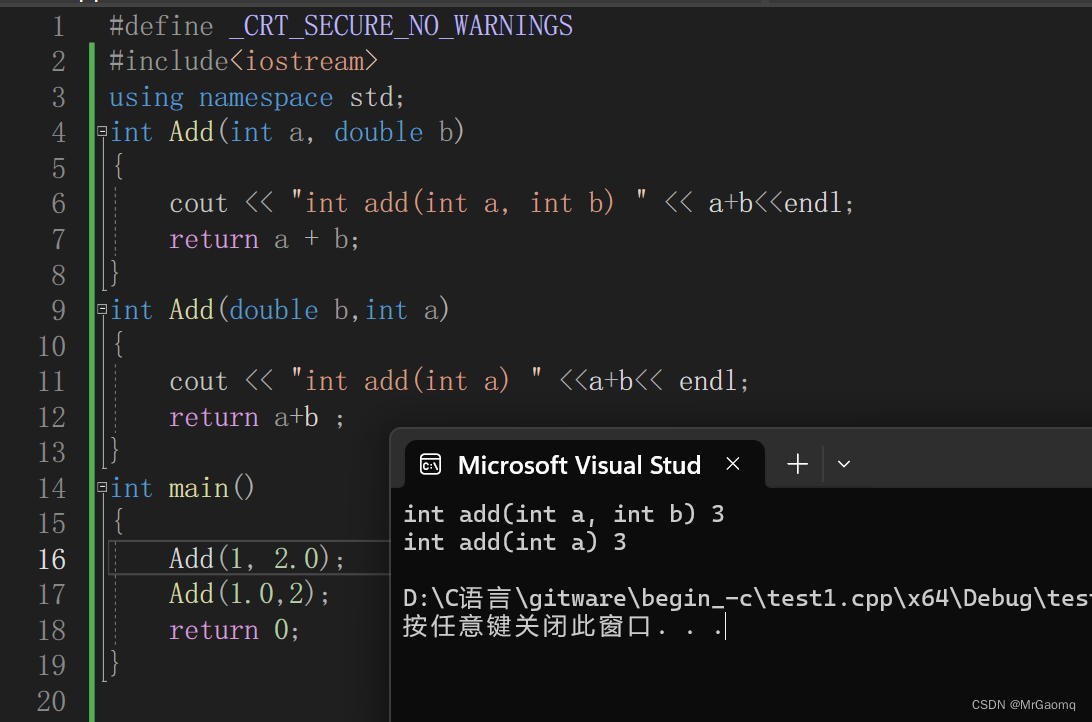
例子3 参数的顺序不同
int Add(int a, double b)
{cout << "int add(int a, int b) " << a+b<<endl;return a + b;
}
int Add(double b,int a)
{cout << "int add(int a) " <<a+b<< endl;return a+b ;
}
int main()
{Add(1, 2.0);Add(1.0,2);return 0;
}
C++支持函数重载的原理–名字修饰(name Mangling)
在上面的缺省函数中有提到过,C/C++中,一个程序要运行起来,需要经历以下几个阶段:预处理、编译、汇编、链接
为什么C++和C语言都要经历这几个阶段,而C++却可以支持函数重载呢?
在C语言实现声明和定义的分离时,如果函数名重复,那么编译器在链接的过程中会根据函数名去找函数的地址,而由于函数名重复,导致分不清具体是要用哪个函数,所以会报链接错误

而C++却可以
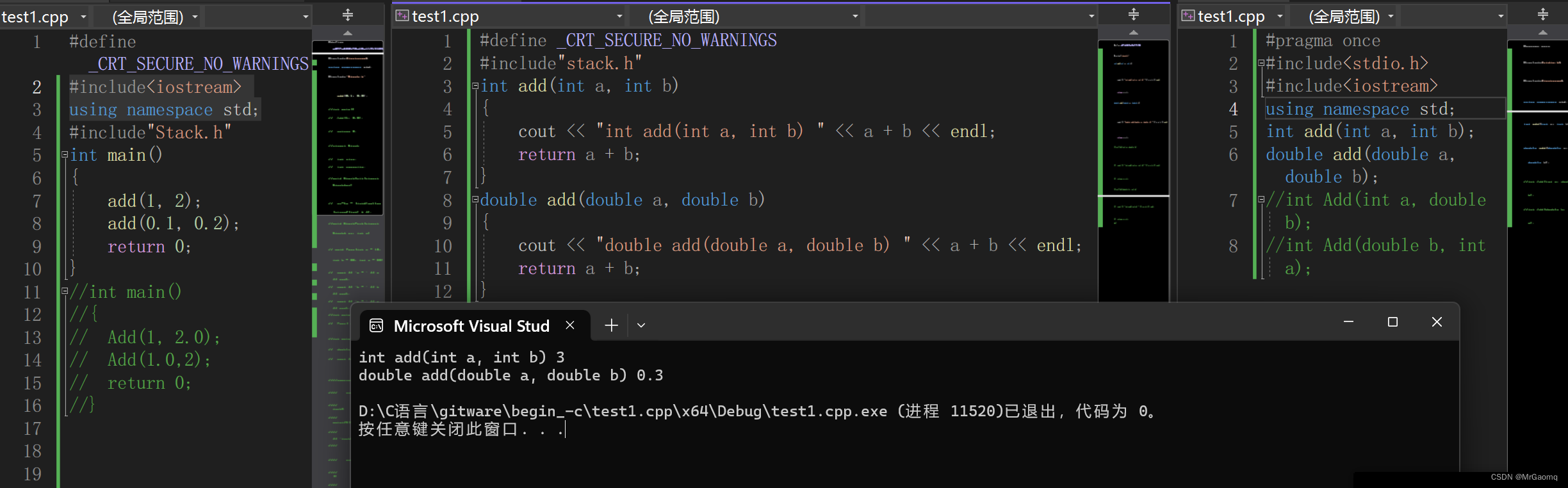
所以C++和C语言在链接部分是有一些不同的
事实上C++在链接中并不是直接用函数名去找地址,而是根据不同的参数类型,返回值的类型等等用一些手段去修饰函数,各个编译器的方式是不一样的
我们以linux为例
int add(int a, int b)
{return a + b;
}
这个函数在修饰后为-Z3addii,其中3为函数名长度,后面两个i为参数类型
double add(double a, double b)
{return a + b;
}
这个函数在修饰后为-Z3adddd