1. 源由

回归是一种监督学习形式，旨在模拟一个或多个输入变量（特征）与一个连续的（目标）变量之间的关系。我们假设输入变量 x 与目标变量 y 之间的关系可以表示为输入的加权和（即，模型在参数上是线性的）。简而言之，线性回归旨在学习一个函数，将一个或多个输入特征映射到单个数值目标值上。

在学习深度神经网络之前，我们将从线性回归的话题开始。

2. 举例 - 波士顿房价

本次将使用波士顿房屋数据集。这个数据集包含了美国人口普查局关于马萨诸塞州波士顿地区房屋的信息。数据集包含了14个独特的属性，其中包括给定郊区的房屋的中位数价值（以千美元为单位）。

接下去使用Keras提供的API进行波士顿房价的一次线性回归解析，基本定义如下：

2.1 获取波士顿房价信息

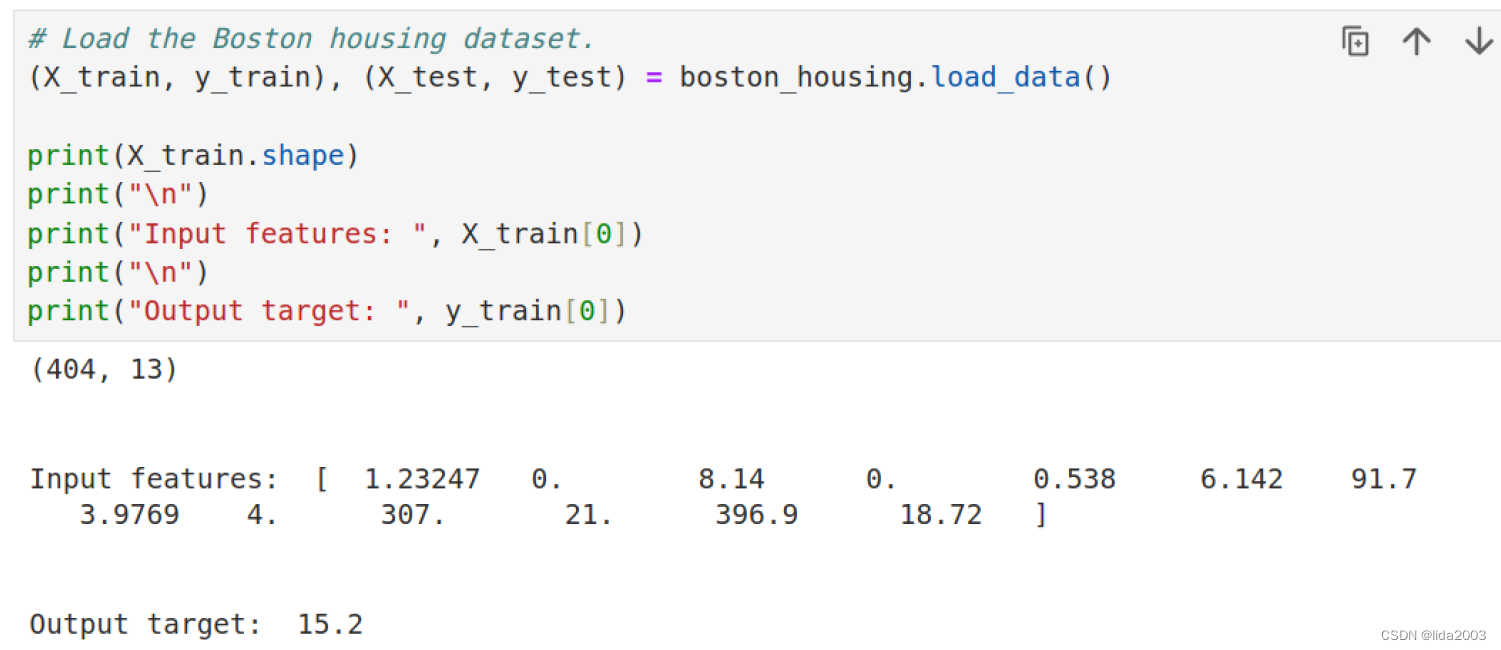
Keras提供了load_data()函数来加载这个数据集。数据集通常被分成训练和测试两个部分，load_data()函数为每个部分返回一个元组。每个元组包含一个特征的二维数组（例如X_train）和一个包含数据集中每个样本的相关目标值的向量（例如y_train）。

从加载的数据中，可以看出，总共404组数据，每组数据有13个特性，1个房价价格。

2.2 抽取波士顿房价和房间数

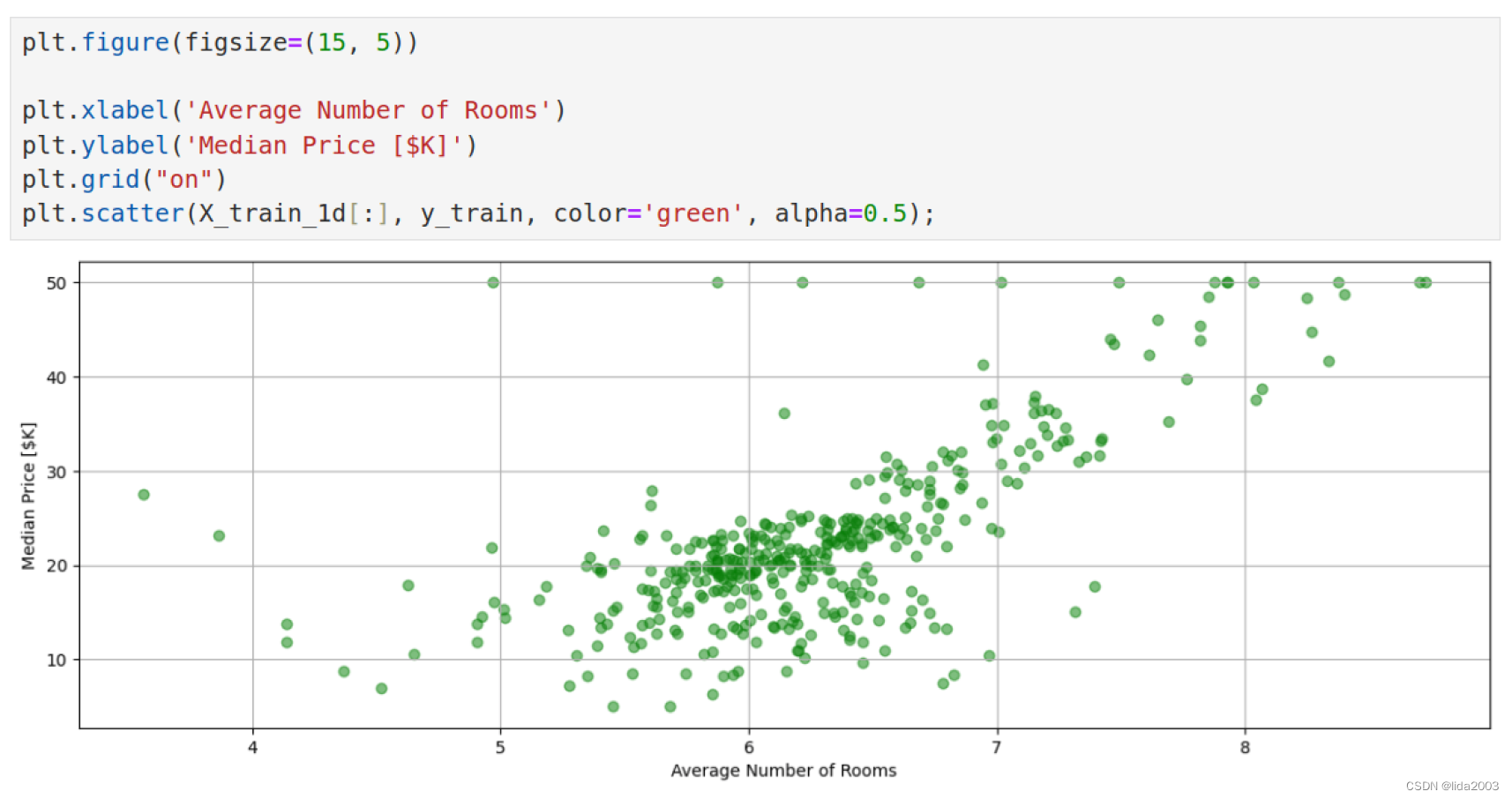
其中第6列为平均房间数，训练数据集404个。

2.3 展示训练集数据

2.4 分析业务逻辑

2.4.1 理解业务

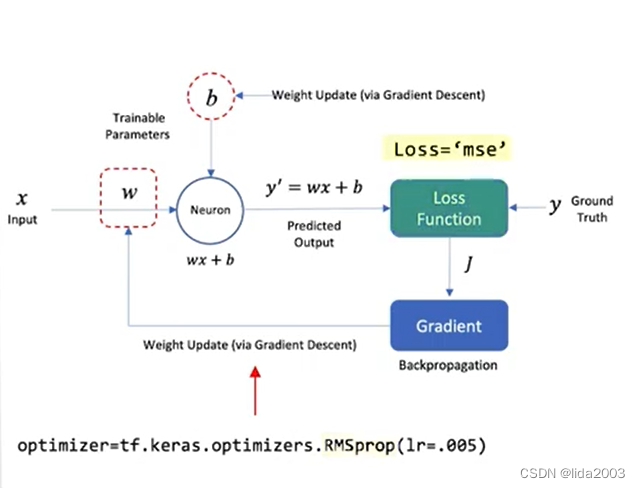
下图展示了如何将这个模型表示为一个具有单个神经元的神经网络。我们将使用这个简单的例子来介绍神经网络的组件和术语。输入数据（x）包含一个特征（房屋的平均房间数），而预测输出（y’）是一个标量（房屋的预测中位价格）。

注：数据集中的每个数据样本表示了波士顿郊区的统计信息。

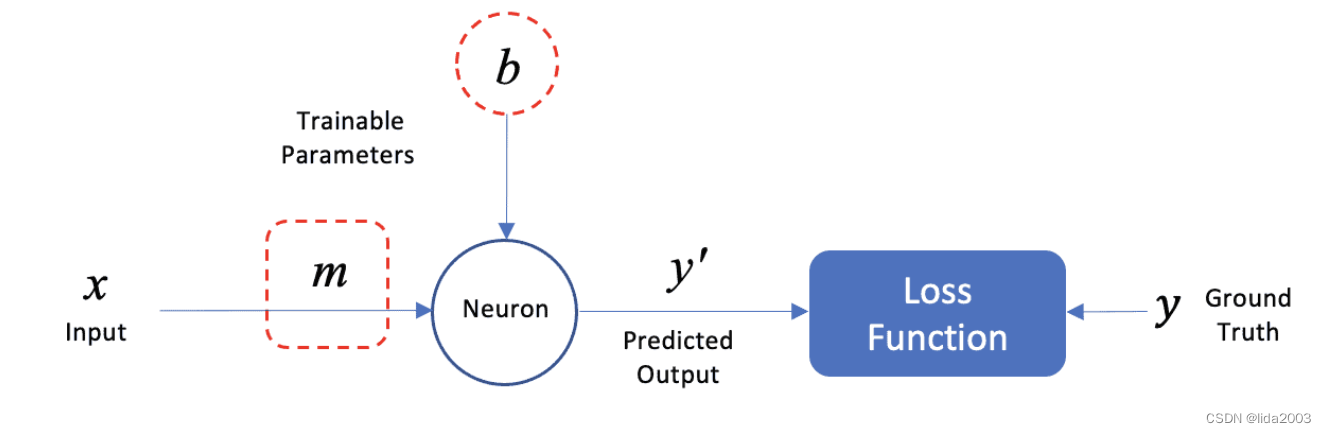
在训练过程中，模型参数（m和b）是通过迭代学习得到的。正如你可能已经知道的那样，模型参数可以通过最小二乘法（OLS）在闭式形式下计算得到。然而，我们也可以使用一种称为梯度下降的数值技术来迭代地解决这个问题，这是神经网络训练的基础。我们在这里不会涵盖梯度下降的细节，但重要的是要理解它是一种迭代技术，用于调整模型的参数。

该网络仅包含一个神经元，它接受单个输入（x）并产生单个输出（y’），即房屋的预测（平均）价格。这个单个神经元有两个可训练的参数，分别是线性模型的斜率（m）和y轴截距（b）。这些参数通常更广泛地被称为权重和偏置。

在回归问题中，模型通常具有多个输入特征，其中每个输入特征都有一个关联的权重（w_i）。然而，在这个例子中，我们将只使用一个输入特征来预测输出。因此，一般来说，一个神经元通常具有多个权重（w_1，w_2，w_3等）和一个单一的偏置项（b）。在这个例子中，你可以将神经元看作是数学计算wx + b，它产生了预测值y’。

2.4.2 参数更新

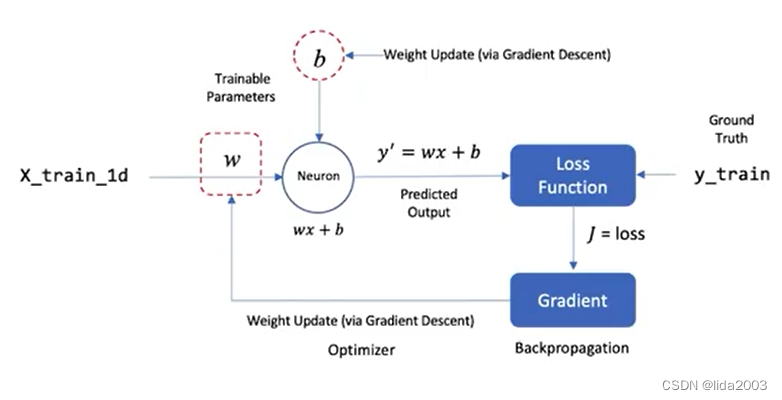
模型参数被初始化为小的随机值。在训练过程中，当训练数据通过网络时，模型的预测值（y’）与数据集中给定样本的真实值（y）进行比较。这些值被用作计算损失的基础，然后作为反馈在网络中，以调整模型参数，从而改善预测结果。

这个权重更新过程涉及两个步骤，称为梯度下降和反向传播。在这个阶段理解这些算法的数学细节并不重要，但重要的是要理解训练模型是一个迭代过程。

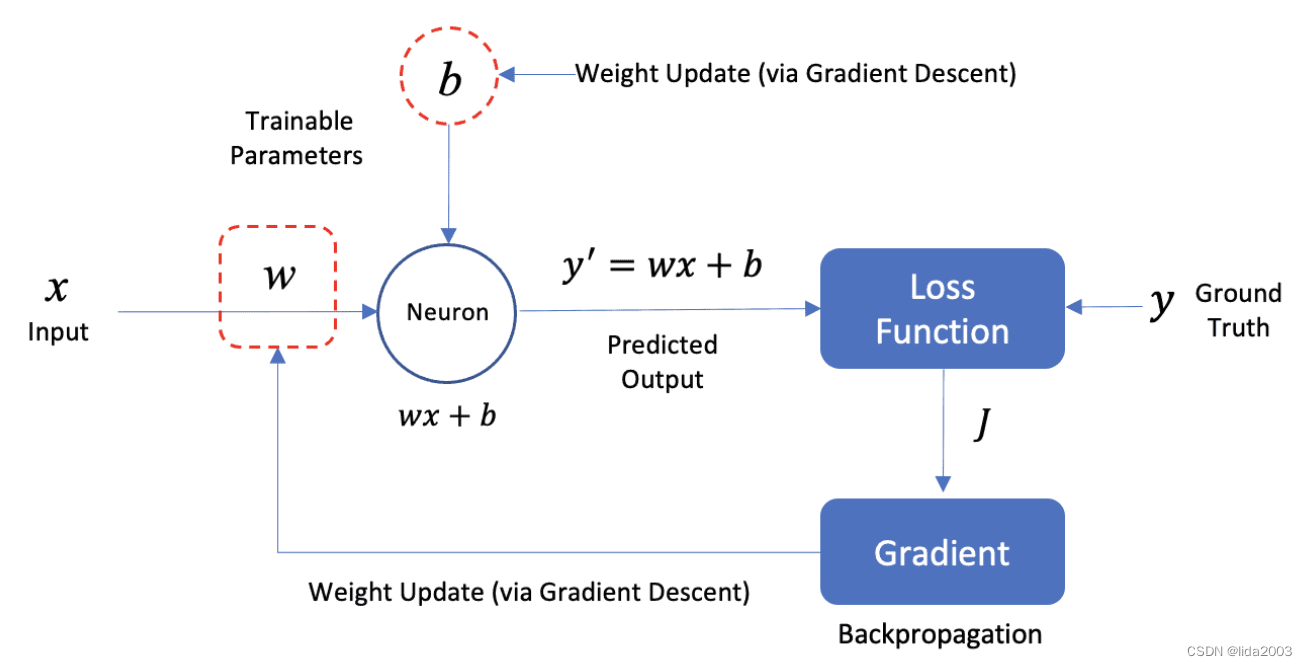
我们使用的损失函数可以有很多形式。在这种情况下，我们将使用均方误差（MSE），这是在回归问题中非常常见的损失函数。

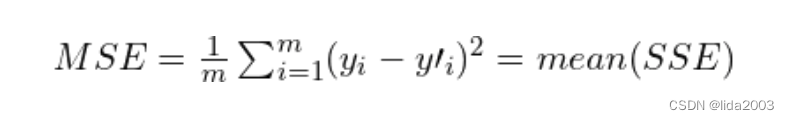基本思想是我们希望最小化这个函数的值，这个函数表示我们的模型与训练数据集之间的误差。在上面的方程中，m 是训练样本的数量。

2.5 Keras建模

2.5.1 定义模型

units=1代表只有一个神经节点；input_shape=(1,)代表只有一个输入参数。

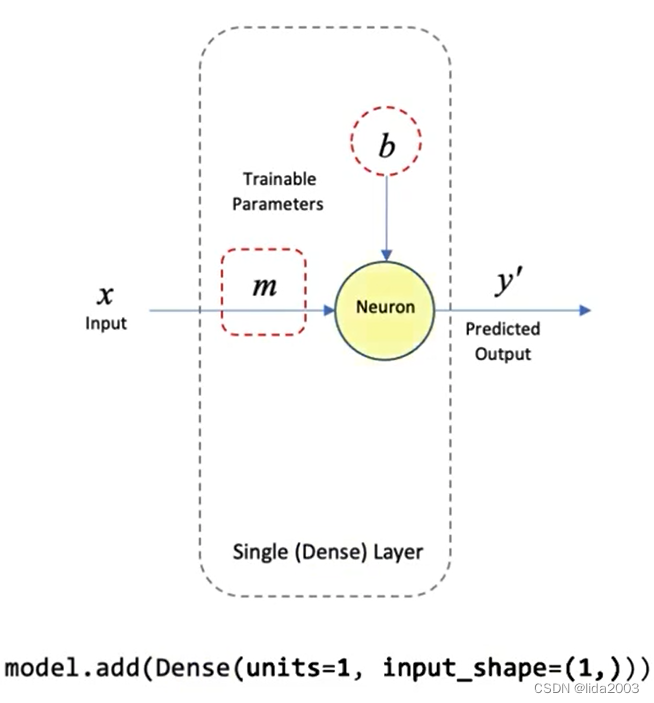
2.5.2 编译模型

通常learning_rate=.005是一个小于1的数，太大可能会振荡，太小收敛的速度太慢，需要权衡。

2.5.3 训练模型

通过不断地迭代，训练模型。

• batch_size批量的数据集
• epochs迭代的次数
• validation_split训练集分割，训练集/验证集

2.5.4 检查迭代损失渐进曲线

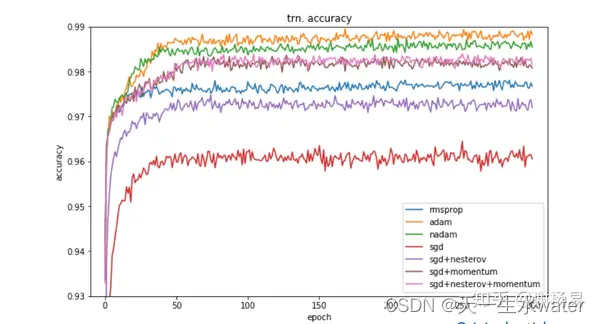
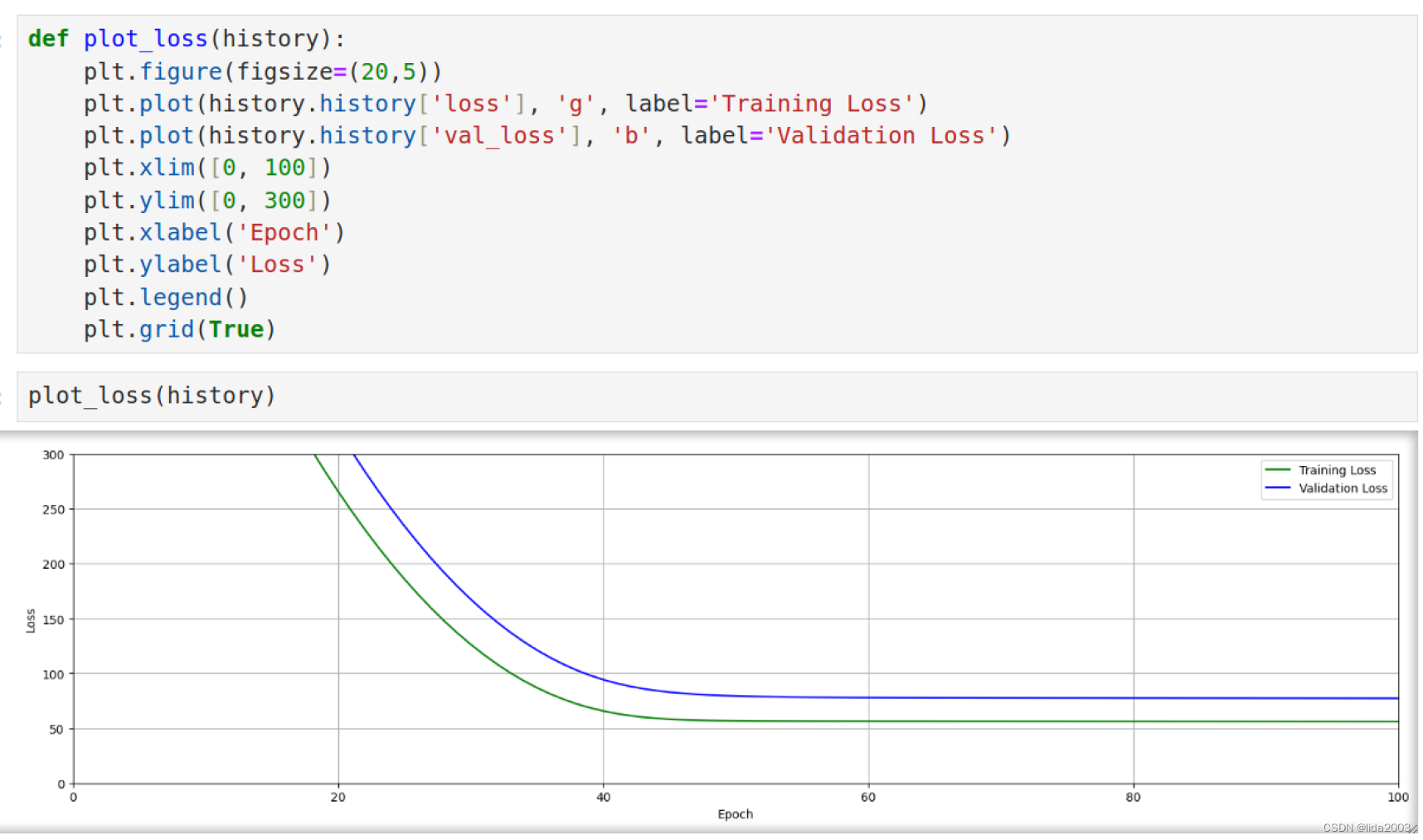上面的损失曲线是相当典型的。首先，注意到有两条曲线，一条是训练损失，另一条是验证损失。两种损失最初都很大，然后逐渐减小，并最终在大约 30 个 epochs 后趋于稳定，不再有进一步的改善。由于模型只是在训练数据上进行训练，训练损失低于验证损失也是相当典型的。

2.6 使用模型进行预测

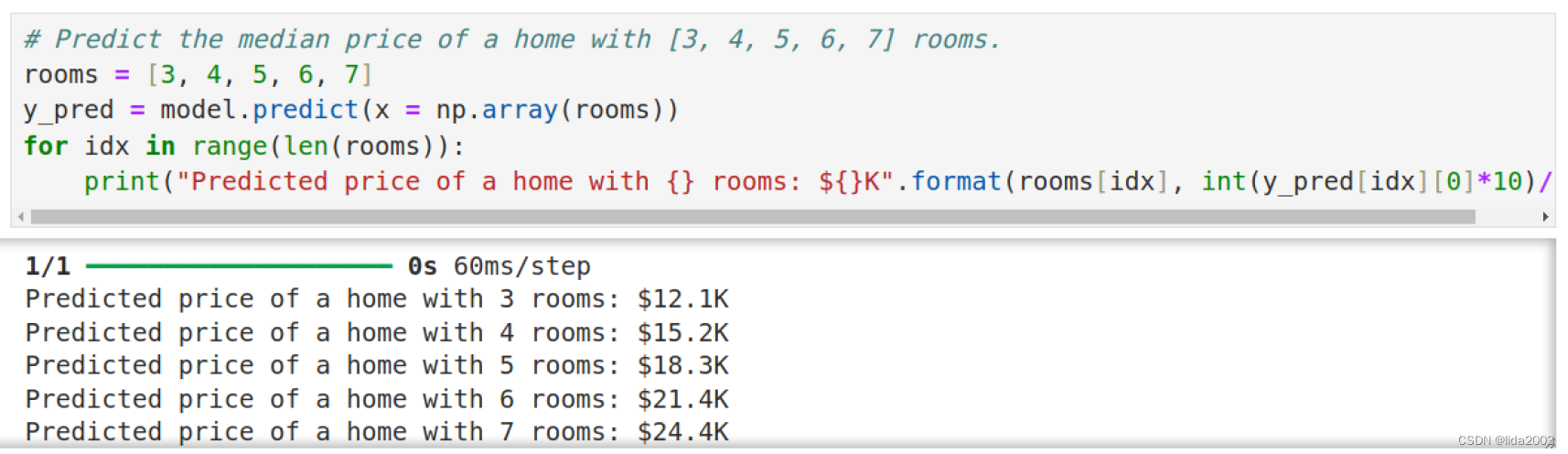
2.7 数据预测

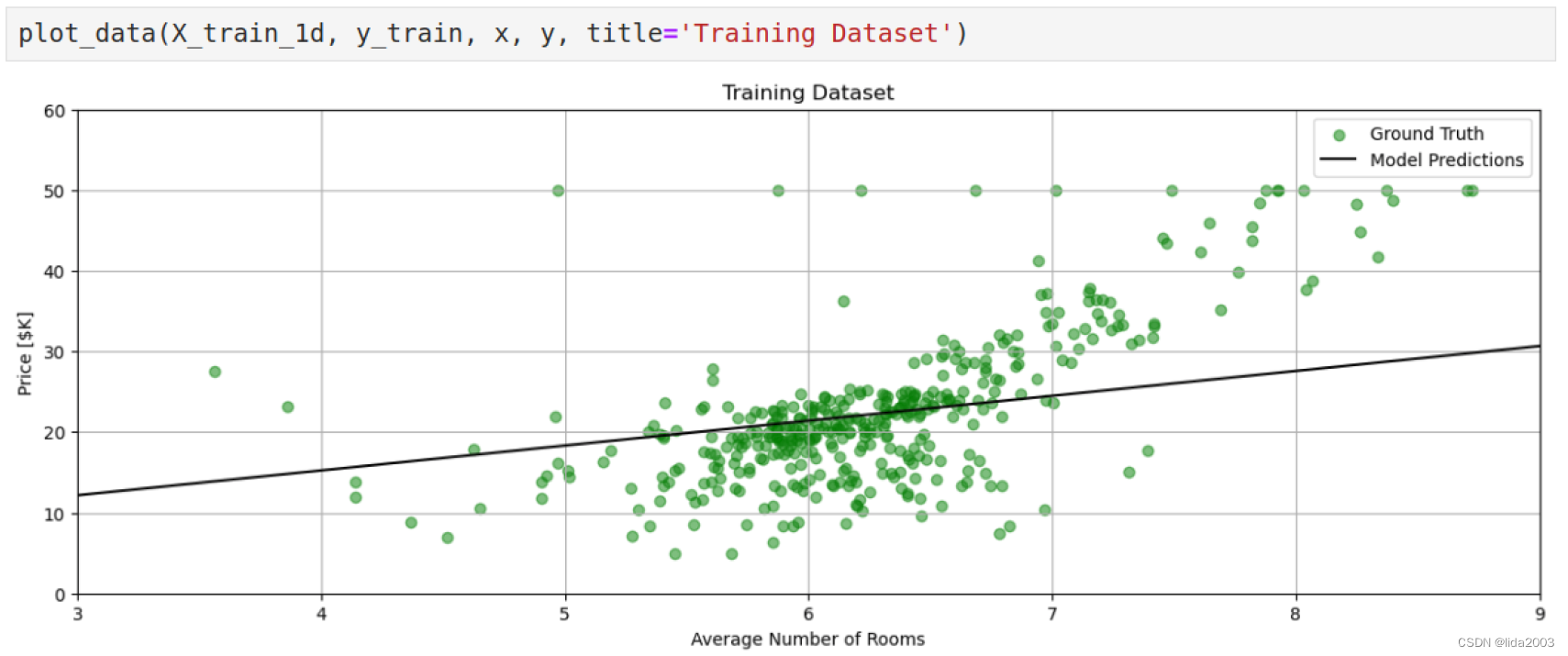
2.7.1 训练数据集 v.s. 线性归一

线性归一，确实有一些拟合，数据平均在两侧都有。

2.7.2 测试数据集 v.s. 线性归一

测试数据集和线性拟合归一似乎有一段距离，貌似斜率不够。

其实这里也可以看出房价并非仅仅与房间数量有关。另外，还可以看出这个拟合归一或者说迭代出来的模型有训练数据集的“记忆”或者说偏置，导致训练数据集并非能很好的均匀分布在线性拟合两边。

3. 步骤抽象

根据上面波士顿房价使用神经网络模型进行线性拟合的例子，可以抽象出以下步骤：

1. 获取数据集（训练/验证）
2. 预处理数据
3. 分析业务逻辑，建立合理的模型
4. 使用Keras建模，并对模型进行评估（损失曲线）
5. 使用模型进行预测

4. 总结

• 数据集的采集需要全面、完整，否则可能产生模型的偏置，尤其是监督式训练。
  

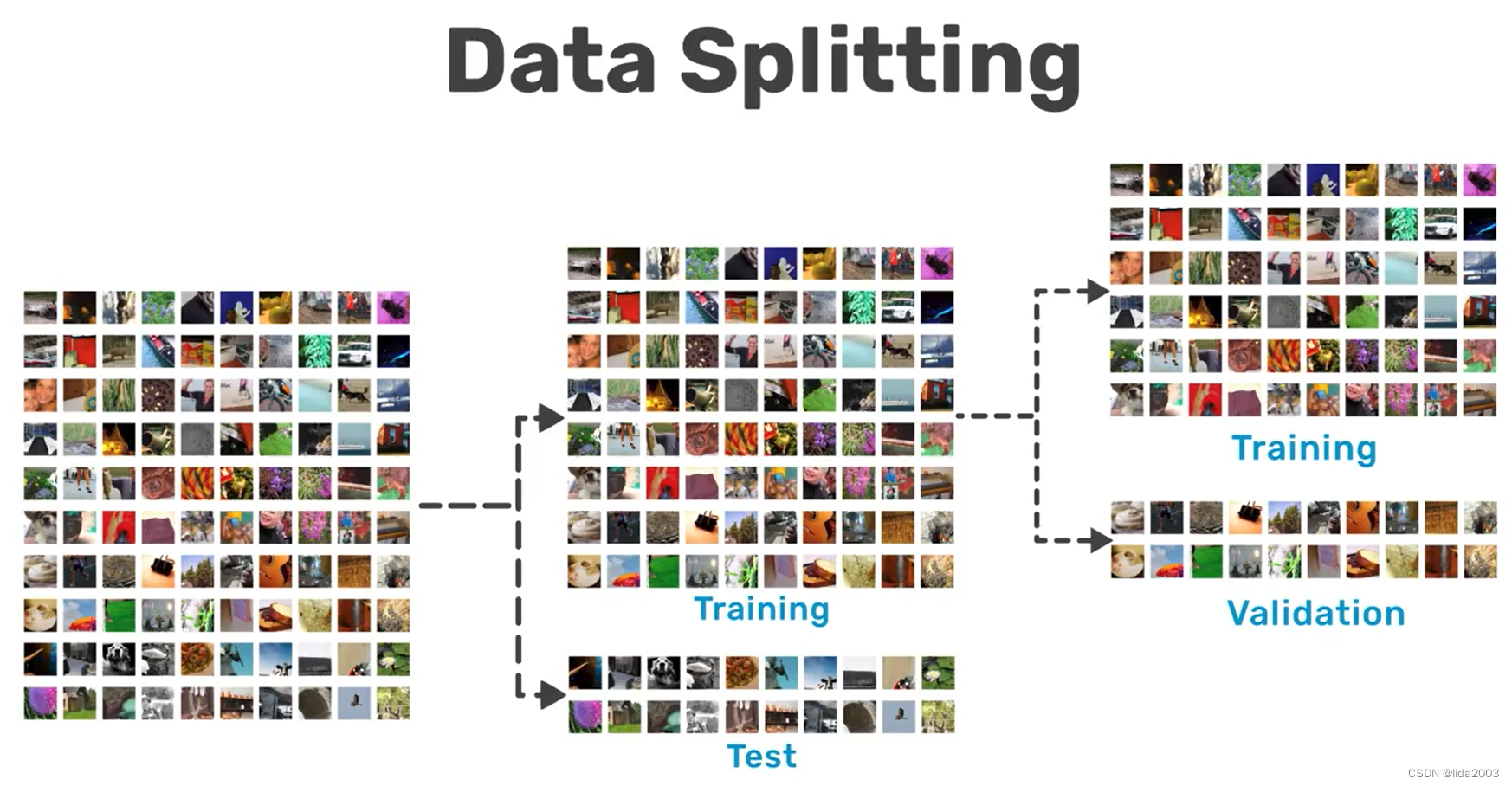
• 一维是在线上渐进，二维则是在平面渐进，当多维的时候，数据将在超平面中渐进，此时的损失函数将会更加复杂，而且并不一定是一个凸面或者凹面

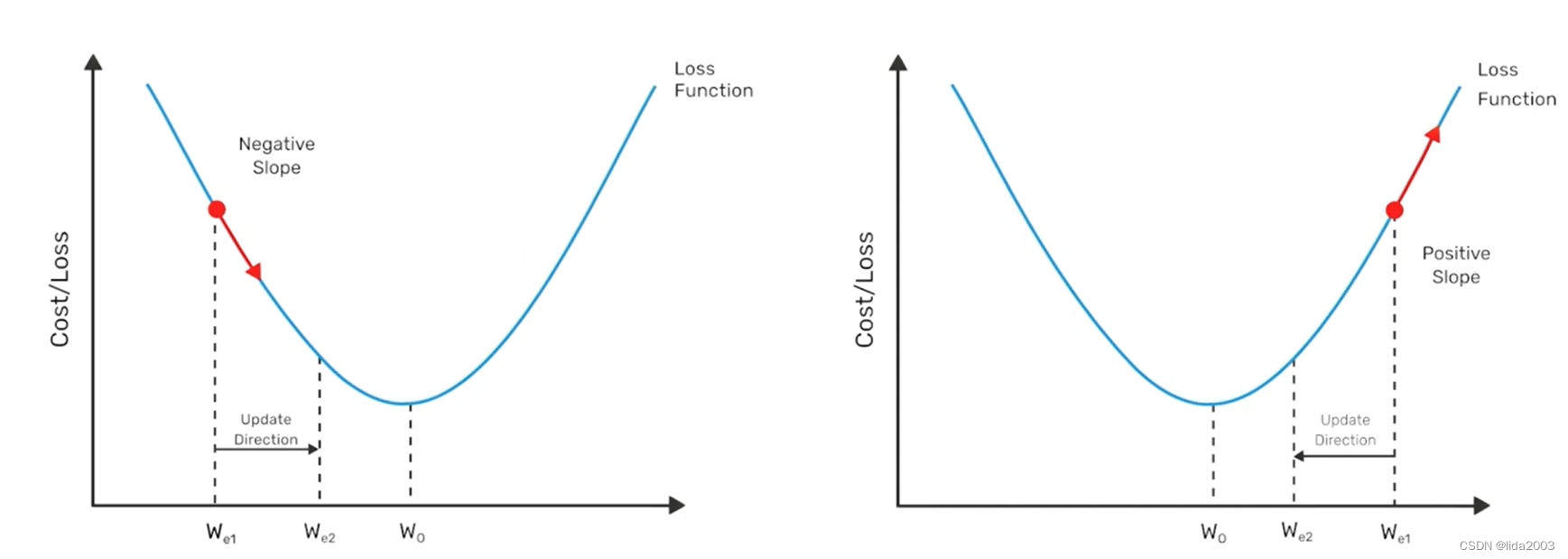
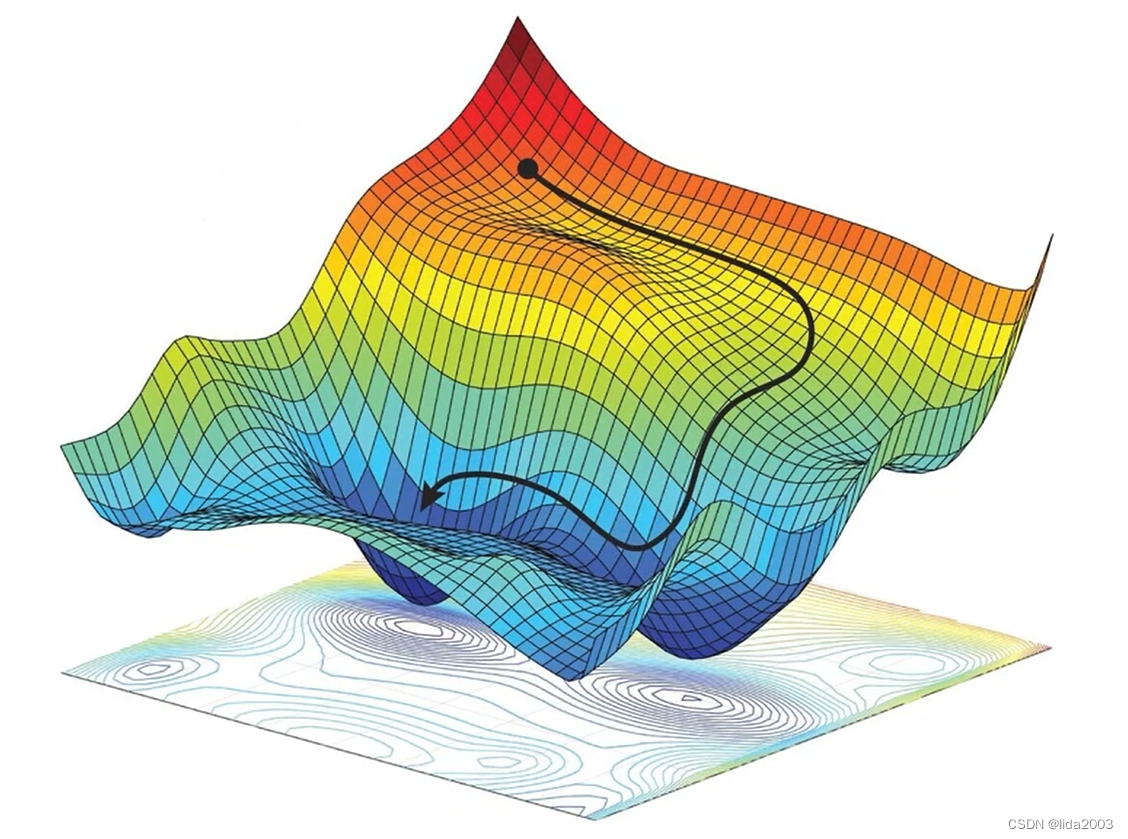
上面展示了如何使用Keras来建模和训练网络以学习线性模型的参数，以及如何可视化模型的预测结果。

测试代码：001_Keras-Linear-Regression

5. 参考资料

【1】Jammy@Jetson Orin - Tensorflow & Keras Get Started