引言

在数据科学中，有很多概念，其中，最容易搞混的就是标量、向量、矩阵、张量了。具体到这些概念的落地实现，又与多维数组有着密不可分的联系。

本文就来尝试对这些概念进行简要地梳理，从而更加清晰地理解这些概念及其关系。

本文的主要内容有：

1、标量与向量

2、矩阵与二维数组

3、张量与多维数组

标量与向量

如果初中数学的知识还没有全部归还给老师，那么对标量和向量的概念，应该还是有些印象的。

标量（Scalar）

所谓标量，是一个单一的数值，起到标识大小的作用，只具有大小，而没有方向。

对应到Python中，它可以是整数、浮点数或者复数等，比如5、-10、3.14159都是标量。

向量（Vector）

所谓向量，最大的特点是既有大小，又有方向。

一个向量，在Python或者NumPy中，可以对应到一个一维数组。数组中的每一个值都是一个标量。

如果将向量放置到空间当中，向量的元素个数，对应到向量所处的空间的维度。

所以，一个具有n个元素的向量，在n维空间中，可以标识为从原点（每个维度的标量值均为0）出发，指向这个向量在n维空间中所对应的点。

矩阵与二维数组

矩阵（Matrix）同样是一个数学概念，通常用于在线性代数中，用来表示一组数字或其他数学对象的矩形数组。

矩阵的元素按行和按列的形式进行排列，通常称为“行”和“列”。在计算机科学中，尤其在数据分析、机器学习和图像处理等领域，矩阵的概念与二维数组是密切相关的。

概括来说，矩阵是一个数据概念，其投射、应用到计算机科学中，对应的实现方式通常是二维数组。比如，我们可以通过NumPy定义一个二维数组来表示矩阵。

在机器学习、深度学习中，会反复应用到矩阵的乘法运算，但是，我们只需要知道矩阵乘法的规则， 就足够应付常见的需求场景了。

矩阵的乘法，必须满足：

(M行，N列) x (N行，L列) = (M行，L列)

感兴趣的同学，可以自行检索补充。

在NumPy中可以通过ndarray来表示矩阵，也可以通过matrix，下面通过代码简单演示一下：

首先创建两个二维数组表示矩阵A和B：

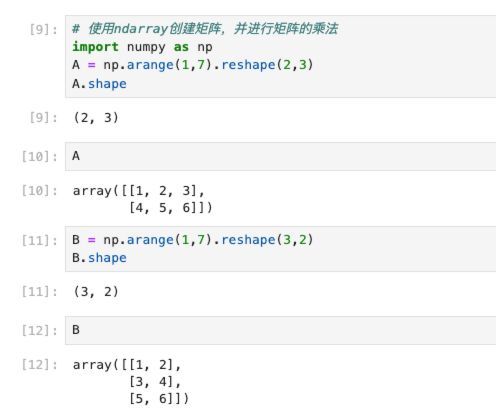
在NumPy中进行基于ndarry的矩阵相乘（点乘）的方法有3种：

1、np.dot(A, B)

2、np.matmul(A, B)

3、A@B

代码如下：

在NumPy中还提供了matrix直接来表示矩阵，这里只是演示一下，通常还是建议使用ndarray：

首先创建两个matrix：

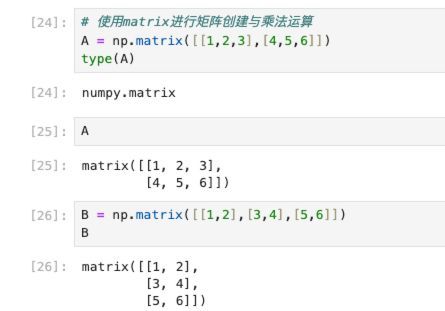
同样有3种方法进行矩阵相乘，np.dot()和np.matmul()两个函数是可以通用的，不同于ndarray，matrix可以直接使用*表示矩阵的点乘运算：

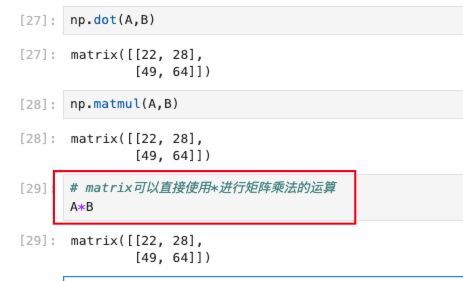
张量与多维数组

如果没有接触过深度学习，可能对“张量”这个概念比较陌生，甚至从未听过。

张量（Tensor）其实是一个更为广泛的数学概念，它通常用于进行多维数据的表示。在机器学习、深度学习和物理学等多个领域中，张量的使用变得越来越普遍。

由于张量是一个更加广泛的概念，因而可以将标量、向量、矩阵的概念进行统一：

1、标量可以看作是0阶张量。

2、向量可以看作是1阶张量。

3、矩阵可以看作是2阶张量。

4、3阶及3阶以上的张量，通常被称之为高阶张量。

可以通过ndarray分别创建不同阶的张量：

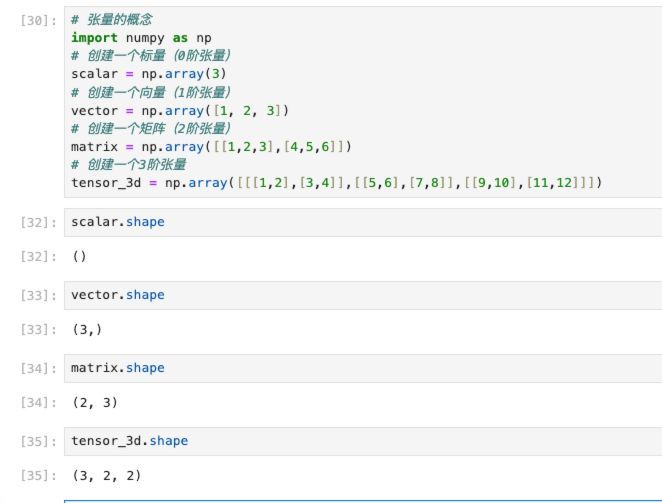
张量概念的底层，同样是基于多维数组进行存储实现。为了便于使用，在Tensorflow和PyTorch等深度学习框架中，张量都是作为最基本的数据结构进行支持的，可以用于表示输入数据、模型参数等。

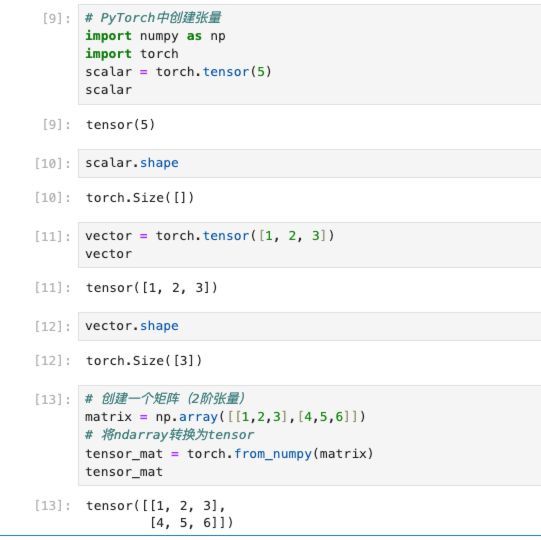
比如，使用PyTorch进行张量的创建：

总结

本文简单辨析了标量、向量、矩阵和张量这几个术语的含义，标量、向量和矩阵可以看作是特殊的张量。所有的张量，在Python、NumPy、PyTorch中，底层可以理解为都是以多维数组的形成进行实现。

以上就是本文的全部内容，感谢您的拨冗阅读！