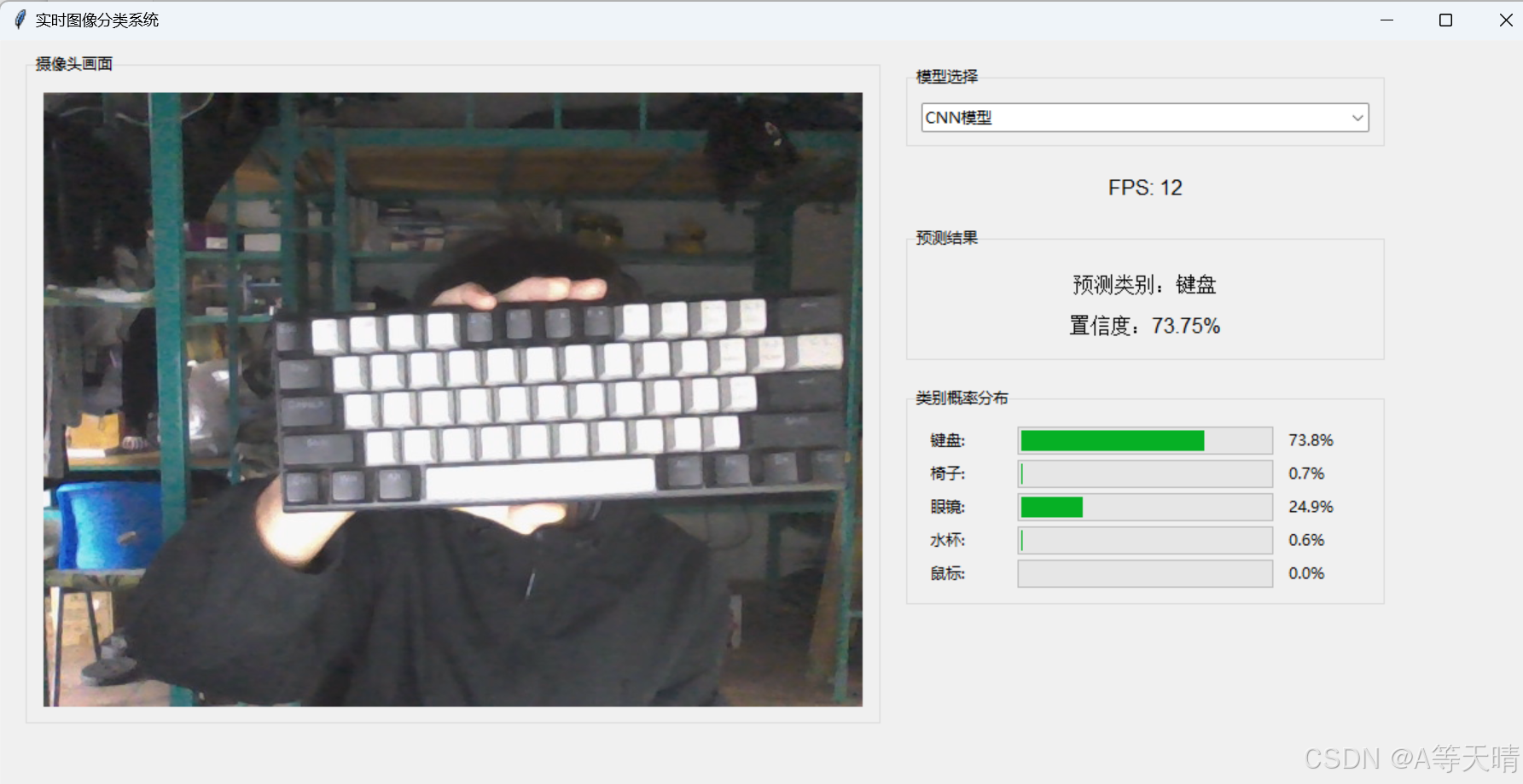
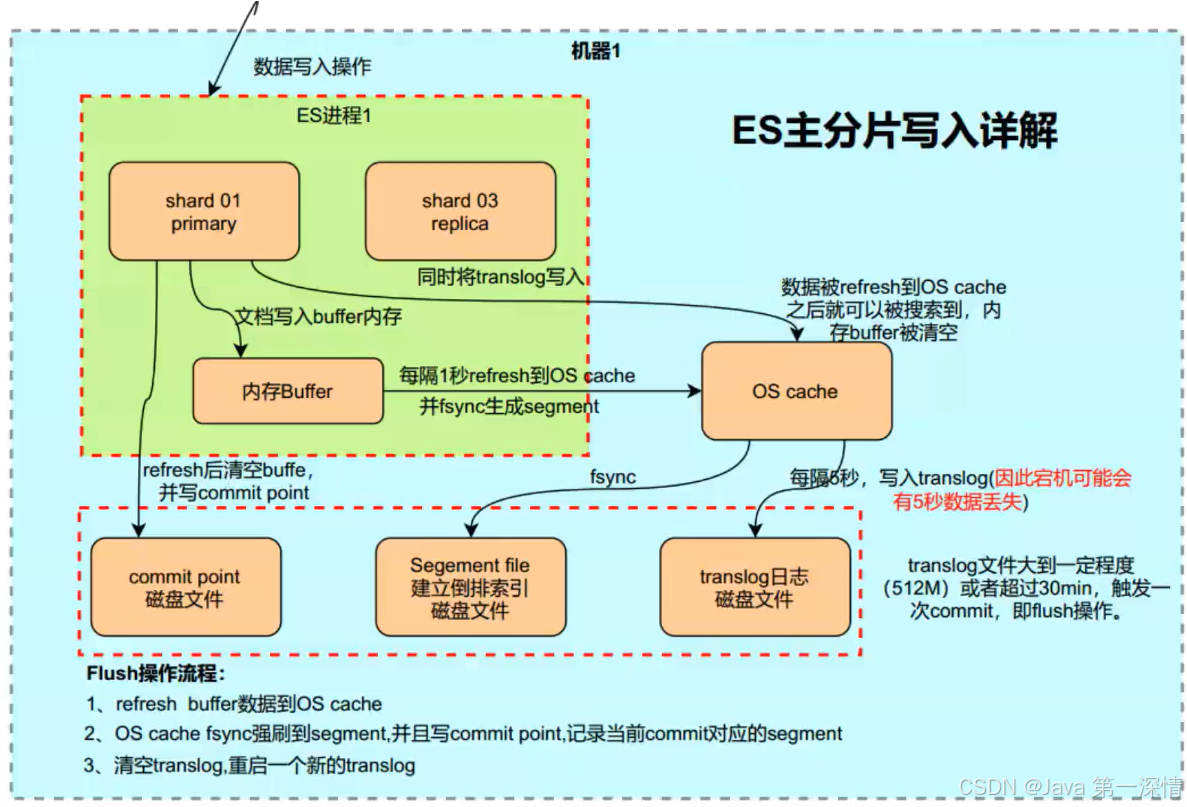
A*v(j) = lambda(j)*v(j)
0,预备环境
编译一份 Lapack源代码,会生成两个 静态链接库:
liblapack.a librefbals.a
1,C版本
源码:
hello.c
/*SSYEVD Example.==============Program computes all eigenvalues and eigenvectors of a real symmetricmatrix A using divide and conquer algorithm, where A is:6.39 0.13 -8.23 5.71 -3.180.13 8.37 -4.46 -6.10 7.21-8.23 -4.46 -9.58 -9.25 -7.425.71 -6.10 -9.25 3.72 8.54-3.18 7.21 -7.42 8.54 2.51Description.============The routine computes all eigenvalues and, optionally, eigenvectors of ann-by-n real symmetric matrix A. The eigenvector v(j) of A satisfiesA*v(j) = lambda(j)*v(j)where lambda(j) is its eigenvalue. The computed eigenvectors areorthonormal.If the eigenvectors are requested, then this routine uses a divide andconquer algorithm to compute eigenvalues and eigenvectors.Example Program Results.========================SSYEVD Example Program ResultsEigenvalues-17.44 -11.96 6.72 14.25 19.84Eigenvectors (stored columnwise)-0.26 0.31 -0.74 0.33 0.42-0.17 -0.39 -0.38 -0.80 0.16-0.89 0.04 0.09 0.03 -0.45-0.29 -0.59 0.34 0.31 0.60-0.19 0.63 0.44 -0.38 0.48
*/
#include <stdlib.h>
#include <stdio.h>/* SSYEVD prototype */
extern void ssyevd_( char* jobz, char* uplo, int* n, float* a, int* lda,float* w, float* work, int* lwork, int* iwork, int* liwork, int* info );
/* Auxiliary routines prototypes */
extern void print_matrix( char* desc, int m, int n, float* a, int lda );/* Parameters */
#define N 5
#define LDA N/* Main program */
int main() {/* Locals */int n = N, lda = LDA, info, lwork, liwork;int iwkopt;int* iwork;float wkopt;float* work;/* Local arrays */float w[N];float a[LDA*N] = {6.39f, 0.00f, 0.00f, 0.00f, 0.00f,0.13f, 8.37f, 0.00f, 0.00f, 0.00f,-8.23f, -4.46f, -9.58f, 0.00f, 0.00f,5.71f, -6.10f, -9.25f, 3.72f, 0.00f,-3.18f, 7.21f, -7.42f, 8.54f, 2.51f};/* Executable statements */printf( " SSYEVD Example Program Results\n" );/* Query and allocate the optimal workspace */lwork = -1;liwork = -1;ssyevd_( "Vectors", "Upper", &n, a, &lda, w, &wkopt, &lwork, &iwkopt,&liwork, &info );lwork = (int)wkopt;work = (float*)malloc( lwork*sizeof(float) );liwork = iwkopt;iwork = (int*)malloc( liwork*sizeof(int) );/* Solve eigenproblem */ssyevd_( "Vectors", "Upper", &n, a, &lda, w, work, &lwork, iwork,&liwork, &info );/* Check for convergence */if( info > 0 ) {printf( "The algorithm failed to compute eigenvalues.\n" );exit( 1 );}/* Print eigenvalues */print_matrix( "Eigenvalues", 1, n, w, 1 );/* Print eigenvectors */print_matrix( "Eigenvectors (stored columnwise)", n, n, a, lda );/* Free workspace */free( (void*)iwork );free( (void*)work );exit( 0 );
} /* End of SSYEVD Example *//* Auxiliary routine: printing a matrix */
void print_matrix( char* desc, int m, int n, float* a, int lda ) {int i, j;printf( "\n %s\n", desc );for( i = 0; i < m; i++ ) {for( j = 0; j < n; j++ ) printf( " %6.2f", a[i+j*lda] );printf( "\n" );}
}2,fortran77 版本
源码:
hello.f
* SSYEVD Example.
* ==============
*
* Program computes all eigenvalues and eigenvectors of a real symmetric
* matrix A using divide and conquer algorithm, where A is:
*
* 6.39 0.13 -8.23 5.71 -3.18
* 0.13 8.37 -4.46 -6.10 7.21
* -8.23 -4.46 -9.58 -9.25 -7.42
* 5.71 -6.10 -9.25 3.72 8.54
* -3.18 7.21 -7.42 8.54 2.51
*
* Description.
* ============
*
* The routine computes all eigenvalues and, optionally, eigenvectors of an
* n-by-n real symmetric matrix A. The eigenvector v(j) of A satisfies
*
* A*v(j) = lambda(j)*v(j)
*
* where lambda(j) is its eigenvalue. The computed eigenvectors are
* orthonormal.
* If the eigenvectors are requested, then this routine uses a divide and
* conquer algorithm to compute eigenvalues and eigenvectors.
*
* Example Program Results.
* ========================
*
* SSYEVD Example Program Results
*
* Eigenvalues
* -17.44 -11.96 6.72 14.25 19.84
*
* Eigenvectors (stored columnwise)
* -0.26 0.31 -0.74 0.33 0.42
* -0.17 -0.39 -0.38 -0.80 0.16
* -0.89 0.04 0.09 0.03 -0.45
* -0.29 -0.59 0.34 0.31 0.60
* -0.19 0.63 0.44 -0.38 0.48
* =============================================================================
*
* .. Parameters ..INTEGER NPARAMETER ( N = 5 )INTEGER LDAPARAMETER ( LDA = N )INTEGER LWMAXPARAMETER ( LWMAX = 1000 )
*
* .. Local Scalars ..INTEGER INFO, LWORK, LIWORK
*
* .. Local Arrays ..INTEGER IWORK( LWMAX )REAL A( LDA, N ), W( N ), WORK( LWMAX )DATA A/$ 6.39, 0.00, 0.00, 0.00, 0.00,$ 0.13, 8.37, 0.00, 0.00, 0.00,$ -8.23,-4.46,-9.58, 0.00, 0.00,$ 5.71,-6.10,-9.25, 3.72, 0.00,$ -3.18, 7.21,-7.42, 8.54, 2.51$ /
*
* .. External Subroutines ..EXTERNAL SSYEVDEXTERNAL PRINT_MATRIX
*
* .. Intrinsic Functions ..INTRINSIC INT, MIN
*
* .. Executable Statements ..WRITE(*,*)'SSYEVD Example Program Results'
*
* Query the optimal workspace.
*LWORK = -1LIWORK = -1CALL SSYEVD( 'Vectors', 'Upper', N, A, LDA, W, WORK, LWORK,$ IWORK, LIWORK, INFO )LWORK = MIN( LWMAX, INT( WORK( 1 ) ) )LIWORK = MIN( LWMAX, IWORK( 1 ) )
*
* Solve eigenproblem.
*CALL SSYEVD( 'Vectors', 'Upper', N, A, LDA, W, WORK, LWORK,$ IWORK, LIWORK, INFO )
*
* Check for convergence.
*IF( INFO.GT.0 ) THENWRITE(*,*)'The algorithm failed to compute eigenvalues.'STOPEND IF
*
* Print eigenvalues.
*CALL PRINT_MATRIX( 'Eigenvalues', 1, N, W, 1 )
*
* Print eigenvectors.
*CALL PRINT_MATRIX( 'Eigenvectors (stored columnwise)', N, N, A,$ LDA )STOPEND
*
* End of SSYEVD Example.
*
* =============================================================================
*
* Auxiliary routine: printing a matrix.
*SUBROUTINE PRINT_MATRIX( DESC, M, N, A, LDA )CHARACTER*(*) DESCINTEGER M, N, LDAREAL A( LDA, * )
*INTEGER I, J
*WRITE(*,*)WRITE(*,*) DESCDO I = 1, MWRITE(*,9998) ( A( I, J ), J = 1, N )END DO
*9998 FORMAT( 11(:,1X,F6.2) )RETURNEND3, Makefile
EXE := hello.c.out hello.f.out
all: $(EXE)%.c.out: %.cgcc $< -o $@ $(LD_FLAGS_C)LD_FLAGS_C := -L /home/hipper/ex_lapack/lapack-3.11 -llapack -lrefblas -lgfortran -lm%.f.out: %.fgfortran -g $< -o $@ $(LD_FLAGS_FORT)LD_FLAGS_FORT := -L /home/hipper/ex_lapack/lapack-3.11/ -llapack -lrefblas.PHONY: clean
clean:-rm -rf $(EXE)4,编译运行

5,参考
mkl