目录
摘要:
简介:
动态规范和定义
动态规格:
双面到单边的功率谱转换
摘要:
模数转换器(adc)代表了接收器、测试设备和其他电子设备中的模拟世界和数字世界之间的联系。正如本文系列的第1部分中所概述的,许多关键的动态参数提供了从给定的ADC中预期的动态性能的准确相关性。本文系列的第2部分介绍了用于测试高速adc的动态规范的一些设置配置、设备建议和测量程序。
简介:
下面讨论测试高速数据转换器的设置和程序。它包括软件工具,硬件配置,数据捕获和分析仪器,需要测试一个新的10位,+3V,高速数据转换器。如果不小心地执行设备选择、设置配置、布局和基于FFT的分析,它还会警告您可能会遇到的陷阱。本文将介绍以下主题。
动态规范和定义
电路板布局及硬件配置
功率谱、箱子、频谱泄漏和窗口功能
用于测试信噪比、SINAD、THD、SFDR和TTIMD的软件工具。
有许多方法可用于从A/D转换器中获取输出数据(而不仅仅是高速转换器),并分析它们的动态性能。这里介绍的方法代表了一种经过验证的方法,并鼓励读者根据手头的应用程序对它们进行修改。
动态规格:
信噪比(SNR)SNRdB = 6.02 × N + 1.76
Signal-to-Noise and Distortion Ratio (SINAD) =20 × log10 (ASIGNAL[rms] / ANOISE[rms]).
ENOB= (SINAD - 1.76) / 6.02
显著的孔径抖动限制了ADC的信噪比性能如下:

其中,fIN为模拟输入频率,tAJ为孔径抖动的时间。时钟抖动对于欠采样的应用程序尤其重要。
功率谱,箱,频谱泄漏和开窗
快速傅里叶变换(FFT)和功率谱是测量和分析来自捕获数据记录的信号的有力工具。它们可以捕获时域信号,测量它们的频率内容,将结果转换为方便的单元,并显示它们。然而,要执行基于FFT的测量,就必须了解这些问题和所涉及的计算。基于FFT的信号分析的基本功能是FFT本身和功率谱。两者都对测量平稳或瞬态信号的频率含量非常有用。fft通常在获取信号的时间间隔内产生一个信号的频率内容的平均值。因此,fft总是被推荐用于平稳信号分析。
双面到单边的功率谱转换
在信号分析中,最基本和最重要的计算方法是使用FFT从双面转换到单侧功率谱,调整频率分辨率,并显示频谱。功率谱通常返回一个包含频域内时域信号功率的双边表示的矩阵。这个矩阵中的值与构成时域信号的每个频率分量的振幅的平方成正比。双侧功率谱的曲线图通常同时包含负频率分量和正频率分量。然而,实际的频率分析工具只关注频谱的正一半,注意到真实信号的频谱是围绕直流电对称的。因此,负频率信息是不相关的。在双边频谱中,一半的能量在正频率,一半在负频率。因此,要将双面频谱转换为单侧频谱,请丢弃矩阵的后半部分,并将每个点(DC除外)乘以2。
箱和频率分辨率
频谱图的x轴和频率范围上的分辨率(见下面的程序代码提取)取决于采样率和数据记录的大小(采集点的数量)。功率谱中的频点或线数为N/2,其中N为时域中捕获的信号点数。功率谱中的第一条频率线总是代表直流电。最后一条频率线可以在fSAMPLE/2 - fSAMPLE/N处找到。频率线以fSAMPLE/N的偶数间隔间隔开,通常被称为频率箱或FFT箱(图3)。

对于fSAMPLE =的采样频率为82.345MHz,记录长度为8192个数据点,FFT图中每条频率线之间的距离正好是10.052kHz。
对频率轴(x轴)的计算证明了采样频率决定了频谱的范围或带宽。对于一个给定的采样频率,在时域中获得的点数决定了分辨率频率。为了提高给定频率范围的分辨率,可以在相同的采样频率下增加数据记录的深度(参见下面的程序代码提取)。
%Find the signal bin number, DC = bin 1
fin=find(Dout_dB(1:numpt/2)==maxdB);
%Span of the input frequency on each side
span=max(round(numpt/200),5);
%Approximate search span for harmonics on each side
spanh=2;
%Determine power spectrum
spectP=(abs(Dout_spect)).×(abs(Dout_spect));
%Find DC offset power
Pdc=sum(spectP(1:span));
%Extract overall signal power
Ps=sum(spectP(fin-span:fin+span));
%Vector/matrix to store both frequency and power of signal and harmonics
Fh=[];
%The 1st element in the vector/matrix represents the signal, the next element represents % the 2nd harmonic, etc.
Ph=[];
光谱泄漏和窗口功能
窗口函数在FFT分析中很常见,而它们的正确使用在基于FFT的分析中是至关重要的量度下面关于频谱泄漏的讨论强调了需要选择一个合适的窗口函数,并为给定的应用程序适当地缩放它。然而,为了准确地确定频谱泄漏,仅仅使用足够的信号采集技术,将双边功率谱转换为单面功率谱,并重新调整结果可能是不够的。为了更好地理解这一项,我们应该在一个频谱纯正弦输入上执行一个n点FFT。
谱泄漏是FFT算法中假设的结果,即时间记录在所有时间中都精确地重复,并且该时间记录中包含的所有信号都是以与时间记录长度对应的间隔为周期的。然而,时间记录(fIN/fSAMPLEn/nwandods)中的非积分循环数违反了这一条件,并导致频谱泄漏(图4)。(请参见第1部分的附录2。)只有两种情况可以保证获得整数个周期:
然而,在大多数情况下,该应用程序处理一个未知的平稳3输入。这意味着不能保证采样是一个整数个的周期。光谱泄漏通过将给定频率分量的能量分散到相邻的频率线或箱上而使测量失真。选择一个合适的窗口函数可以尽量减少这种频谱泄漏的影响。

为了充分理解一个给定的窗口函数如何影响频谱,我们必须更仔细地观察窗口的频率特征。输入数据的窗口化相当于将原始信号的频谱与窗口的频谱进行卷积。即使对于相干采样4,信号也与均匀高度的矩形窗口进行卷积。
窗口的实频特征是由一个主叶和几个侧叶组成的连续频谱。主叶以时域内信号的每个频率分量为中心。侧瓣在主瓣的每一侧的间隔接近于零。另一方面,FFT产生一个离散的频谱。窗口的连续周期谱由FFT采样,就像ADC在时域采样输入信号一样。在FFT的每条频率线上出现的是每个FFT频率线上的连续卷积谱的值。
如果原始信号的频率分量与频率线完全匹配,就像当您获得一个整数周期时一样,您只看到频谱的主瓣。侧叶不出现,因为窗口光谱在主叶两侧的箱式频率间隔上趋近于零。如果时间记录不包含整数周期,则窗口的连续谱从主瓣中心移到频率箱的一部分,该频率箱对应于频率分量和FFT频率线之间的差值。这种变化导致侧裂片出现在光谱中。因此,窗口的侧叶特征直接影响相邻频率分量“泄漏”到相邻频率箱的程度。
窗口特征
在选择适当的窗口之前,有必要定义允许用户比较窗口的参数和特征。这些特征包括-3dB主叶宽度、-6dB主叶宽度、最大侧叶水平和侧叶翻转率(表1)。窗口的侧叶的特征是侧叶峰值的最大侧叶水平(定义为最大侧叶水平)和侧叶水平(定义为以dB/十年或频率八度为单位的渐近衰减率)。
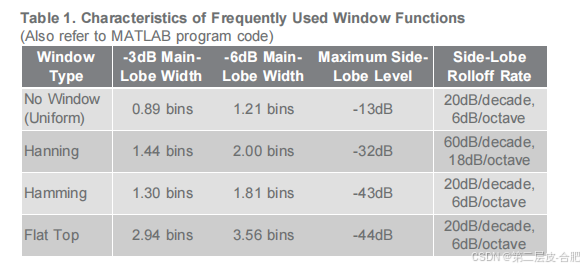
窗口的侧叶的特征是侧叶峰值的最大侧叶水平(定义为最大侧叶水平)和侧叶波动(定义为以dB/十年或频率八度为单位的渐近衰减率)。
选择正确得窗口
不同的窗口适合不同的应用程序。要选择正确的光谱窗口,就必须猜测信号的频率内容。如果信号包含远离感兴趣的频率的强干扰频率分量,那么您应该选择一个侧叶具有高滚动率的窗口。如果强干扰信号接近感兴趣的频率,则侧叶最大水平较低的窗口更合适。
如果感兴趣的频带包含两个或两个以上彼此接近的信号,则具有光谱分辨率变得很重要。在这种情况下,带有狭窄主叶的窗口更好。对于单个频率分量,其中的焦点是振幅精度,而不是其精确的位置在频率箱,推荐一个具有宽主叶的窗口。最后,建议对平面或宽带频谱进行相干采样(而不是窗口)(请参见下面的程序代码提取)。
汉宁窗口函数具有良好的频率分辨率和降低频谱泄漏,在大多数应用中都得到令人满意的结果。平顶窗口具有良好的振幅精度,但其宽的主叶提供了较差的频率分辨率和更多的光谱泄漏。平顶窗口的最大侧瓣水平比汉宁窗口更低,但汉宁窗口有更快的滚动率。
一个只由瞬态信号组成的应用程序应该完全没有光谱窗口,因为它们倾向于在样本块的开始时衰减重要的信息。在瞬态信号的情况下,您应该选择一个非光谱窗口,如力或指数窗口。选择一个合适的窗口并不容易,但如果信号内容未知,就可以从汉宁特性开始。比较多个窗口函数的性能以找到最适合给定应用程序的函数也是一个很好的主意
动态范围规格信噪比、SINAD、THD和SFDR
SNR = 10×log10(Ps/Pn)
SINAD = 10×log10(Ps/(Pn+Pd))
THD = 10×log10(Pd/Ph(1))
SFDR = 10×log10(Ph(1)/max(Ph(2:10))),
其中Ps为信号功率,Pn为噪声功率,Pd为2阶至5阶谐波引起的失真功率,Ph (1)为基本谐波功率,Ph(2:10)为2阶至9次谐波的谐波功率(功率谱水平见下面的程序代码提取)。
基于MATLAB源代码(见下文),MAX1448不仅对其数据表规格进行了测试,而且还对许多其他过采样和过采样的输入频率进行了测试。它在所有条件下都取得了良好的动态性能。






