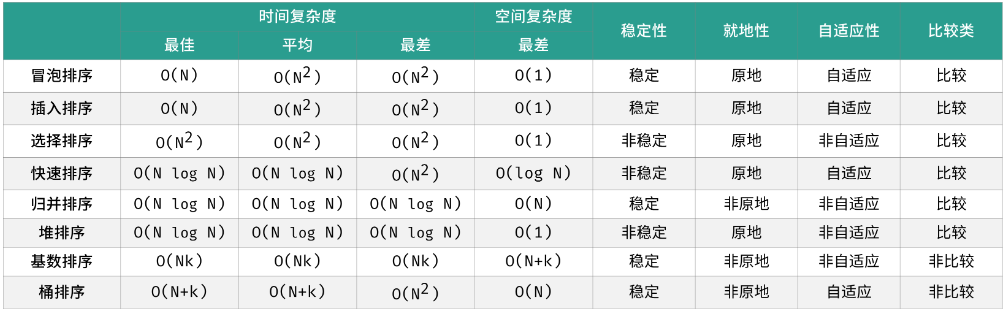
- How to choose:
- 如果对时间复杂度要求比较高并且键的分布范围比较广,可以使用归并排序、快速排序和堆排序。
- 如果不能使用额外的空间,那么快速排序和堆排序都是不错的选择。
- 如果规定了排序的键的范围,可以优先考虑使用桶排序。
- 如果不想写太多的代码同时时间复杂度没有太高的要求,可以考虑冒泡排序、选择排序和插入排序。
- 如果排序的过程中没有复杂的额外操作,直接使用编程语言内置的算法>排序算法就行了。
冒泡排序
从前往后(或从后往前比较两个元素,若逆序则交换)
- 内循环(相邻双指针比较) + 外循环(重复内循环)
- 标志位优化:如果在某轮内循环中未执行任何交换操作,说明数组已经完成排序,直接返回结果
public int[] BubbleSort(int[] nums) {int n = nums.length;for(int i = 0; i < n - 1; i++){boolean flag = false;for(int j = 0; j < n - i - 1; j++){ // 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端if(nums[j] > nums[j+1]){int tmp = nums[j];nums[j] = nums[j+1];nums[j+1] = tmp;flag = true;}}if(!flag) break; //此轮“冒泡”未交换任何元素,直接跳出}return nums;
}
选择排序
在待排序元素中选取最小(最大)的元素加入序列
与冒泡排序的区别是:冒泡在每个内循环都会交换,而选择只会在外循环交换
public int[] sortArray(int[] nums) {int n = nums.length;for(int i = 0; i < n; i++){int min = i;for(int j = i + 1; j < n; j++){if(nums[j] < nums[min]) min = j;}if(min != i){int tmp = nums[i];nums[i] = nums[min];nums[min] = tmp;}}return nums;
}
插入排序
遍历整个数组,保持左侧的始终是排序好的数组,将当前元素插入到左侧对应的位置。
void insertionSort(int[] nums) {// 外循环:已排序区间为 [0, i-1]for (int i = 1; i < nums.length; i++) {int base = nums[i], j = i - 1;// 内循环:将 base 插入到已排序区间 [0, i-1] 中的正确位置while (j >= 0 && nums[j] > base) {nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位j--;}nums[j + 1] = base; // 将 base 赋值到正确位置}
}
希尔排序
进行多次的、间隔的插入排序
public int[] sortArray(int[] nums) {int n = nums.length;int gap = n >> 1; // gap首先取nums.length的一半while (gap > 0) {for (int index = 0; index < gap; index++) { //多次的//间隔的for (int i = index + gap; i < n; i += gap) {int j = i;while (j > index && nums[j] < nums[j - gap]) {int tmp = nums[j];nums[j] = nums[j - gap];nums[j - gap] = tmp;j -= gap;}}}gap >>= 1; // gap除2}return nums;
}
归并排序
分治思想:将两个或多个已经有序的序列合并成一个
先划分【中点处】后合并
void mergeSort(int[] nums, int left, int right) {if (left >= right) return; // 当子数组长度为 1 时终止递归// 划分int mid = (left + right) / 2; // 中点处mergeSort(nums, left, mid); // 递归左子数组mergeSort(nums, mid + 1, right); // 递归右子数组// 合并merge(nums, left, mid, right);
}/* 合并左子数组和右子数组 */
void merge(int[] nums, int left, int mid, int right) {// 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]// 创建一个临时数组 tmp ,用于存放合并后的结果int[] tmp = new int[right - left + 1];// 初始化左子数组和右子数组的起始索引int i = left, j = mid + 1, k = 0;// 当左右子数组都还有元素时,进行比较并将较小的元素复制到临时数组中while (i <= mid && j <= right) {if (nums[i] <= nums[j])tmp[k++] = nums[i++];elsetmp[k++] = nums[j++];}// 将左子数组和右子数组的剩余元素复制到临时数组中while (i <= mid) {tmp[k++] = nums[i++];}while (j <= right) {tmp[k++] = nums[j++];}// 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间for (k = 0; k < tmp.length; k++) {nums[left + k] = tmp[k];}
}
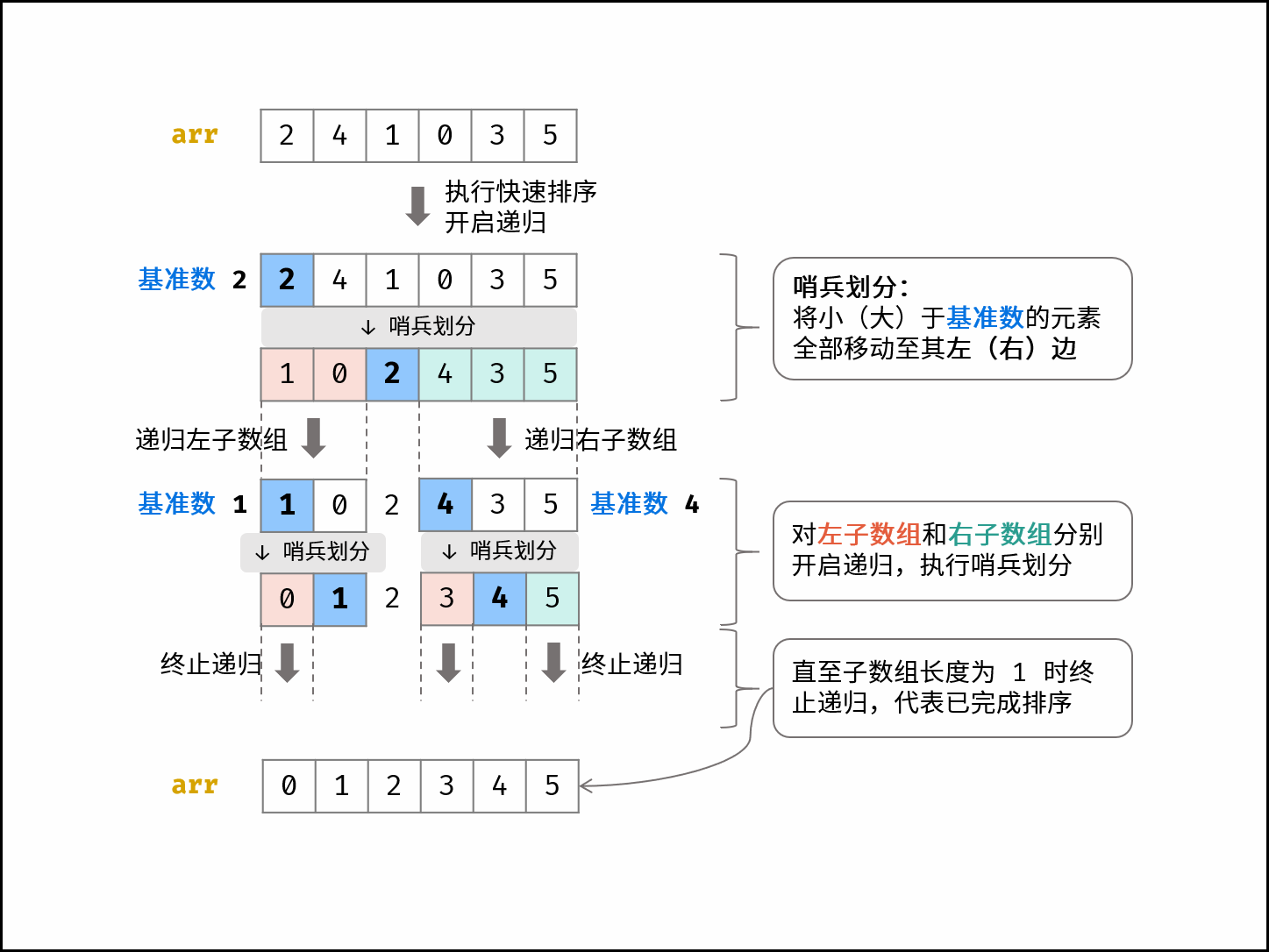
快速排序
- 取一个枢轴
pivot作为基准值- 哨兵划分:将大于
pivot的值排到右边,小于pivot的值排到左边- 递归左子表:重复步骤1、2
- 递归右子表:重复步骤1、2
public int[] sortArray(int[] nums) {int l = 0, r = nums.length - 1;quickSort(nums, l, r);return nums;
}
void quickSort(int[] nums, int l, int r){if(l >= r) return;int pivot = partition(nums, l, r); // 步骤2quickSort(nums, l, pivot - 1); // 步骤3quickSort(nums, pivot + 1, r); // 步骤4
}
int partition(int[] nums, int l, int r){int i = l, j = r; //步骤1:选取最左边元素为pivotwhile(i < j){while(i < j && nums[j] >= nums[l]) j--; //大的放左边while(i < j && nums[i] <= nums[l]) i++; //小的放右边swap(nums, i, j);}swap(nums, l, i);return i;
}
void swap(int[] nums, int i, int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;return;
}
- 优化:
-
随机
pivot:在数组中选取三个候选元素(通常为数组的首、尾、中点元素),并将这三个候选元素的中位数作为pivot。【解决输入数组是完全倒序的最差情况】 -
尾递归:每轮递归时,仅对 较短的子数组 执行哨兵划分 partition() 【完全有序的输入数组在每次划分时占用栈帧空间大】
-
public int[] sortArray(int[] nums) {int l = 0, r = nums.length - 1;quickSort(nums, l, r);return nums;
}
void quickSort(int[] nums, int l, int r){if(l >= r) return;int pivot = partition(nums, l, r); // 步骤2// 😊尾递归优化if (pivot - l < r - pivot) {quickSort(nums, l, pivot - 1); // 递归排序左子数组l = pivot + 1; // 剩余未排序区间为 [pivot + 1, r]} else {quickSort(nums, pivot + 1, r); // 递归排序右子数组r = pivot - 1; // 剩余未排序区间为 [l, pivot - 1]}
}
// 😊随机pivot优化
/* 选取三个候选元素的中位数 */
int medianThree(int[] nums, int left, int mid, int right) {int l = nums[left], m = nums[mid], r = nums[right];if ((l <= m && m <= r) || (r <= m && m <= l))return mid; // m 在 l 和 r 之间if ((m <= l && l <= r) || (r <= l && l <= m))return left; // l 在 m 和 r 之间return right;
}int partition(int[] nums, int l, int r){// 😊随机pivot优化int m = medianThree(nums, l, (l + r) / 2, r); // 选取三个候选元素的中位数swap(nums, l, m); // 将中位数交换至数组最左端int i = l, j = r; //步骤1:选取最左边元素为pivotwhile(i < j){while(i < j && nums[j] >= nums[l]) j--; //大的放左边while(i < j && nums[i] <= nums[l]) i++; //小的放右边swap(nums, i, j);}swap(nums, l, i);return i;
}
void swap(int[] nums, int i, int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;return;
}
- 快排为什么快:
- 虽然快速排序的最差时间复杂度为 O ( n 2 ) O(n^2) O(n2),没有归并排序稳定,但在绝大多数情况下,快速排序能在 O ( n log n ) O(n \text{log}n) O(nlogn)的时间复杂度下运行,出现最差情况的概率很低。
- 在执行哨兵划分操作时,系统可将整个子数组加载到缓存,因此访问元素的效率较高。而像“堆排序”这类算法需要跳跃式访问元素,从而缺乏这一特性,缓存使用效率较低。
- 快速排序的比较、赋值、交换等操作的总数量最少,复杂度的常数系数小。
堆排序
- 建大顶堆
- 循环:交换堆顶元素和堆底元素 —> 堆长度-1 ——>自顶向下调整堆(即堆化)
- n - 1次循环后 升序排序完成
void heapSort(int[] nums) {// 建堆操作:堆化除叶节点以外的其他所有节点for (int i = nums.length / 2 - 1; i >= 0; i--) {siftDown(nums, nums.length, i);}// 从堆中提取最大元素,循环 n-1 轮for (int i = nums.length - 1; i > 0; i--) {// 交换根节点与最右叶节点(交换首元素与尾元素)int tmp = nums[0];nums[0] = nums[i];nums[i] = tmp;// 以根节点为起点,从顶至底进行堆化siftDown(nums, i, 0);}
}/* 堆的长度为 n ,从节点 i 开始,从顶至底堆化 */
void siftDown(int[] nums, int n, int i) {while (true) {// 判断节点 i, l, r 中值最大的节点,记为 maint l = 2 * i + 1, int r = 2 * i + 2;int ma = i;if (l < n && nums[l] > nums[ma]) ma = l;if (r < n && nums[r] > nums[ma]) ma = r;// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出if (ma == i) break;// 交换两节点int temp = nums[i];nums[i] = nums[ma];nums[ma] = temp;// 循环向下堆化i = ma;}
}