1143.最长公共子序列

力扣题目链接(opens new window)

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

• 输入：text1 = "abcde", text2 = "ace"
• 输出：3
• 解释：最长公共子序列是 "ace"，它的长度为 3。

示例 2:

• 输入：text1 = "abc", text2 = "abc"
• 输出：3
• 解释：最长公共子序列是 "abc"，它的长度为 3。

示例 3:

• 输入：text1 = "abc", text2 = "def"
• 输出：0
• 解释：两个字符串没有公共子序列，返回 0。

提示:

• 1 <= text1.length <= 1000
• 1 <= text2.length <= 1000 输入的字符串只含有小写英文字符。

本题和 718.最长重复子数组 区别在于这里不要求是连续的了，但要有相对顺序，即："ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

继续动规五部曲分析如下：

• 确定dp数组（dp table）以及下标的含义

dp[i][j]：长度为[0, i - 1]的字符串 text1 与长度为[0, j - 1]的字符串 text2 的最长公共子序列为dp[i][j]

有同学会问：为什么要定义长度为[0, i - 1]的字符串text1，定义为长度为[0, i]的字符串text1不香么？

这样定义是为了后面代码实现方便，如果非要定义为长度为[0, i]的字符串 text1 也可以，其实就是简化了dp数组第一行和第一列的初始化逻辑。

• 确定递推公式

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

代码如下：

java">if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;
} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}

• dp数组如何初始化

先看看dp[i][0]应该是多少呢？

test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;

同理dp[0][j]也是0。

其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

代码：

java">int[][] dp = new int[text1.length() + 1][text2.length() + 1];

• 确定遍历顺序

从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：

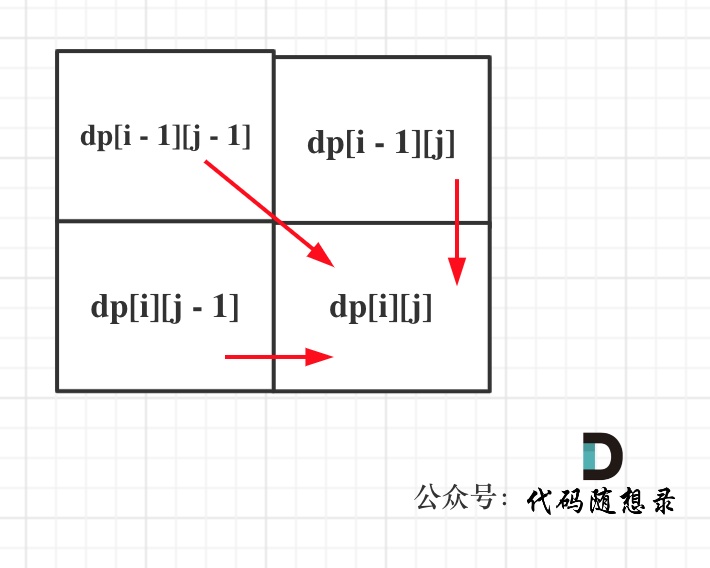
那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

• 举例推导dp数组

以输入：text1 = "abcde", text2 = "ace" 为例，dp状态如图：

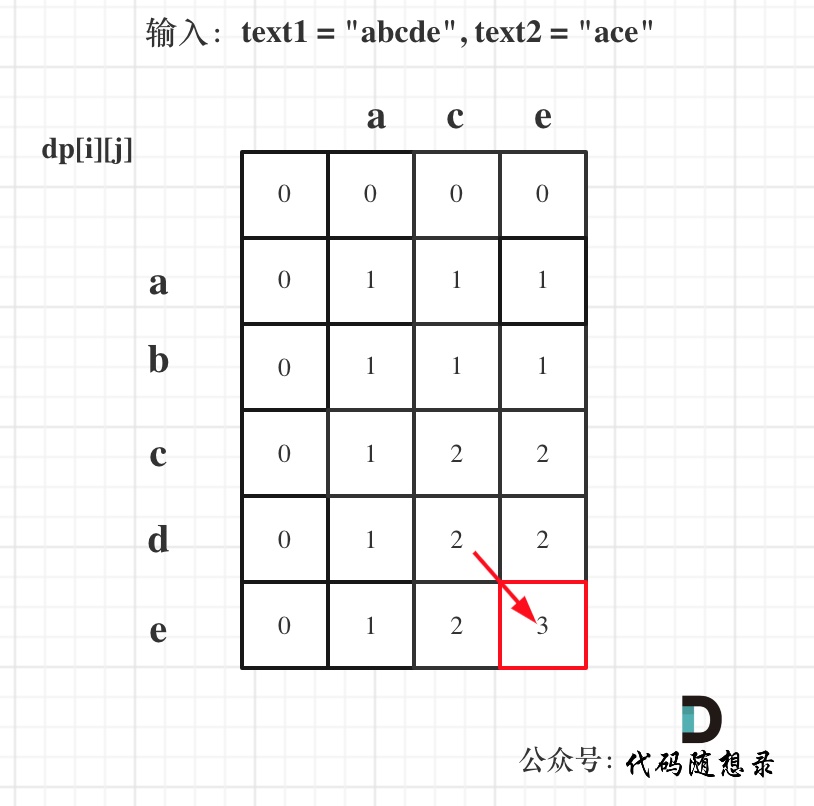
最后红框dp[text1.length][text2.length]为最终结果

以上分析完毕，Java代码如下：

java">class Solution {public int longestCommonSubsequence(String text1, String text2) {// char[] char1 = text1.toCharArray();// char[] char2 = text2.toCharArray();// 可以在一開始的時候就先把text1, text2 轉成char[]，之後就不需要有這麼多爲了處理字串的調整int[][] dp = new int[text1.length() + 1][text2.length() + 1]; // 先对dp数组做初始化操作for (int i = 1 ; i <= text1.length() ; i++) {char char1 = text1.charAt(i - 1);for (int j = 1; j <= text2.length(); j++) {char char2 = text2.charAt(j - 1);if (char1 == char2) { // 开始列出状态转移方程dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[text1.length()][text2.length()];}
}

• 时间复杂度: O(n * m)，其中 n 和 m 分别为 text1 和 text2 的长度
• 空间复杂度: O(n * m)

java">class Solution {public int longestCommonSubsequence(String text1, String text2) {int n1 = text1.length();int n2 = text2.length();// 多从二维dp数组过程分析  // 关键在于  如果记录  dp[i - 1][j - 1]// 因为 dp[i - 1][j - 1]  <!=>  dp[j - 1]  <=>  dp[i][j - 1]int [] dp = new int[n2 + 1];for(int i = 1; i <= n1; i++){// 这里pre相当于 dp[i - 1][j - 1]int pre = dp[0];for(int j = 1; j <= n2; j++){//用于给pre赋值int cur = dp[j];if(text1.charAt(i - 1) == text2.charAt(j - 1)){//这里pre相当于dp[i - 1][j - 1]   千万不能用dp[j - 1] !!dp[j] = pre + 1;} else{// dp[j]     相当于   dp[i - 1][j]// dp[j - 1] 相当于   dp[i][j - 1]dp[j] = Math.max(dp[j], dp[j - 1]);}//更新dp[i - 1][j - 1], 为下次使用做准备pre = cur;}}return dp[n2];}
}

---

1035.不相交的线

力扣题目链接(opens new window)

我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。

现在，我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且我们绘制的直线不与任何其他连线（非水平线）相交。

以这种方法绘制线条，并返回我们可以绘制的最大连线数。

相信盆友看到这道题目都没啥思路，我们来逐步分析一下。

绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！

直线不能相交，这就是说明在字符串A中 找到一个与字符串 B 相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。

拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：

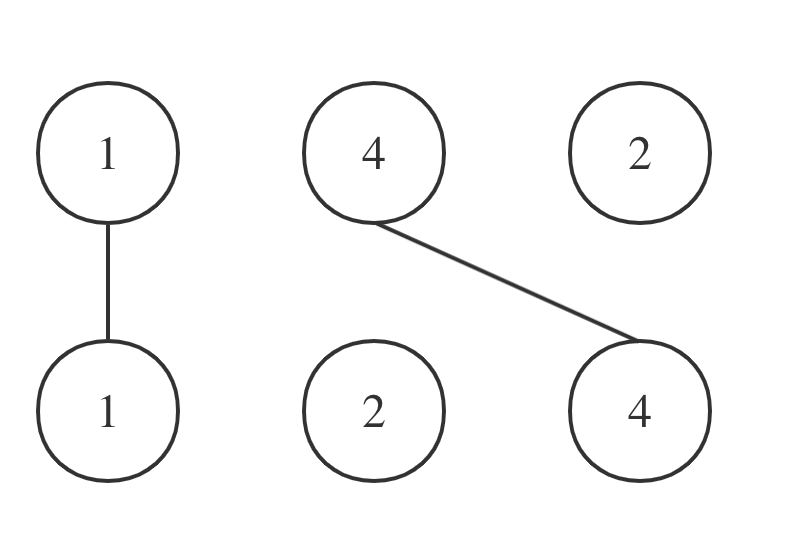
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）

这么分析完之后，大家可以发现：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

那么本题就和我们刚刚讲过的上一道题目 1143.最长公共子序列 就是一样一样的了。

一样到什么程度呢？ 把字符串名字改一下，其他代码都不用改，直接copy过来就行了。

所以本题我就不再做动规五部曲分析了。

java">class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int len1 = nums1.length;int len2 = nums2.length;int[][] dp = new int[len1 + 1][len2 + 1];for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[len1][len2];}
}

总结

看到代码大家也可以发现其实就是求两个字符串的最长公共子序列，但如果没有做过 1143.最长公共子序列，本题其实还有很有难度的。

大家会发现一个正确的刷题顺序对算法学习是非常重要的！

---

53. 最大子序和

力扣题目链接(opens new window)

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

• 输入: [-2,1,-3,4,-1,2,1,-5,4]
• 输出: 6
• 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

这道题之前我们在讲解贪心专题的时候用贪心算法解决过一次，贪心算法：最大子序和。

这次我们用动态规划的思路再来分析一次。

动规五部曲如下：

• 确定dp数组（dp table）以及下标的含义

dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。

• 确定递推公式

dp[i]只有两个方向可以推出来：

• dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
• nums[i]，即：从头开始计算当前连续子序列和

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

• dp数组如何初始化

从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。

dp[0]应该是多少呢?

根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。

• 确定遍历顺序

递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。

• 举例推导dp数组

以示例一为例，输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，对应的dp状态如下： 

动态规划）" height="239" src="https://img-blog.csdnimg.cn/img_convert/af2ab1628c37c83b69e504662eefb7f6.png" width="450" />

注意最后的结果可不是dp[nums.size() - 1]！，而是dp[6]。

在回顾一下dp[i]的定义：包括下标i之前的最大连续子序列和为dp[i]。

那么我们要找最大的连续子序列，就应该找每一个 i 为终点的连续最大子序列。

所以在递推公式的时候，可以直接选出最大的dp[i]。

以上动规五部曲分析完毕，完整代码如下：

java"> /*** 1.dp[i]代表当前下标对应的最大值* 2.递推公式 dp[i] = max (dp[i-1]+nums[i],nums[i]) res = max(res,dp[i])* 3.初始化 都为 0* 4.遍历方向，从前往后* 5.举例推导结果。。。** @param nums* @return*/public static int maxSubArray(int[] nums) {if (nums.length == 0) {return 0;}int res = nums[0];int[] dp = new int[nums.length];dp[0] = nums[0];for (int i = 1; i < nums.length; i++) {dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);res = res > dp[i] ? res : dp[i];}return res;}

• 时间复杂度：O(n)
• 空间复杂度：O(n)

总结

这道题目用贪心也很巧妙，但有一点绕，需要仔细想一想。动规的解法还是很直接的。

---

392.判断子序列

力扣题目链接(opens new window)

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

示例 1：

• 输入：s = "abc", t = "ahbgdc"
• 输出：true

示例 2：

• 输入：s = "axc", t = "ahbgdc"
• 输出：false

提示：

• 0 <= s.length <= 100
• 0 <= t.length <= 10^4

两个字符串都只由小写字符组成。

（这道题也可以用双指针的思路来实现，时间复杂度也是O(n)）

这道题应该算是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

所以掌握本题的动态规划解法是对后面要讲解的编辑距离的题目打下基础。

动态规划五部曲分析如下：

• 确定dp数组（dp table）以及下标的含义

dp[i][j] 表示以下标 i-1 为结尾的字符串s，和以下标 j-1 为结尾的字符串 t，相同子序列的长度为dp[i][j]。

注意这里是判断 s 是否为 t 的子序列。即 t 的长度是大于等于 s 的。

有同学问了，为啥要表示下标 i-1 为结尾的字符串呢，为啥不表示下标i为结尾的字符串呢？

其实用 i 来表示也可以！

但我统一以下标 i-1 为结尾的字符串来计算，这样在下面的递归公式中会容易理解一些，如果还有疑惑，可以继续往下看。

• 确定递推公式

在确定递推公式的时候，首先要考虑如下两种操作，整理如下：

• if (s[i - 1] == t[j - 1])
  • t 中找到了一个字符在 s 中也出现了
• if (s[i - 1] != t[j - 1])
  • 相当于 t 要删除元素，继续匹配

if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1;，因为找到了一个相同的字符，相同子序列长度自然要在dp[i-1][j-1]的基础上加1（如果不理解，在回看一下dp[i][j]的定义）

if (s[i - 1] != t[j - 1])，此时相当于 t 要删除元素，t 如果把当前元素 t[j - 1] 删除，那么 dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];

其实这里 大家可以发现和 ​​​​​​​1143.最长公共子序列 的递推公式基本那就是一样的，区别就是 本题 如果删元素一定是字符串 t，而 1143.最长公共子序列 是两个字符串都可以删元素。

• dp数组如何初始化

从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。

这里大家已经可以发现，在定义dp[i][j]含义的时候为什么要表示以下标 i-1 为结尾的字符串 s，和以下标 j-1 为结尾的字符串 t，相同子序列的长度为dp[i][j]。

因为这样的定义在dp二维矩阵中可以留出初始化的区间，如图：

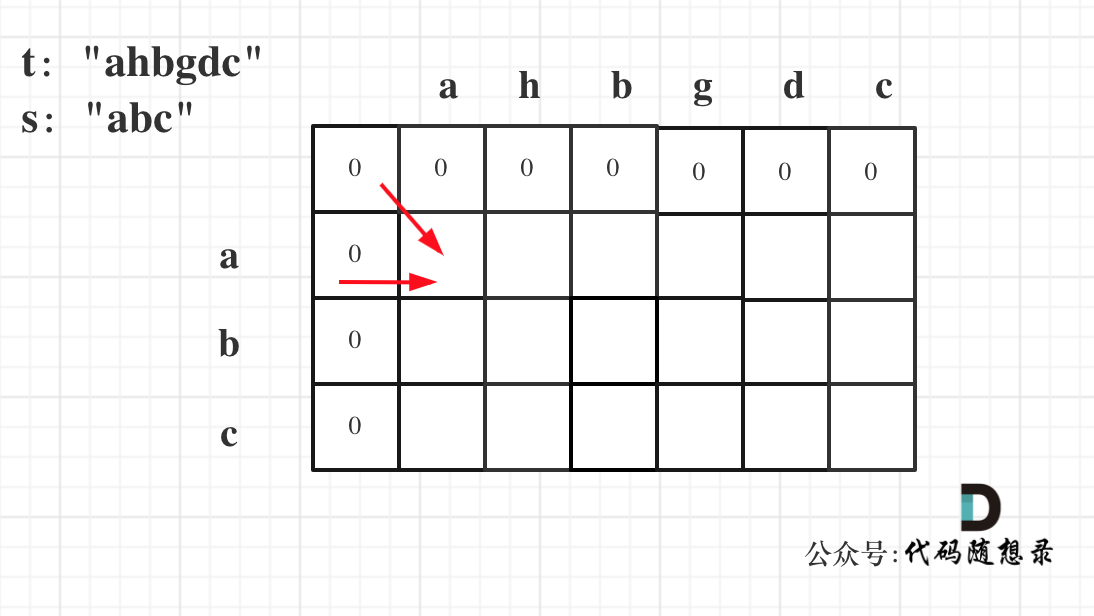
如果要是定义的dp[i][j]是以下标 i 为结尾的字符串 s 和以下标 j 为结尾的字符串 t，初始化就比较麻烦了。

dp[i][0] 表示以下标 i-1 为结尾的字符串，与空字符串的相同子序列长度，所以为0。

dp[0][j]同理。

Java中数组默认初始化为0，所以可以不用单独赋值

java">int[][] dp = new int[length1+1][length2+1];

• 确定遍历顺序

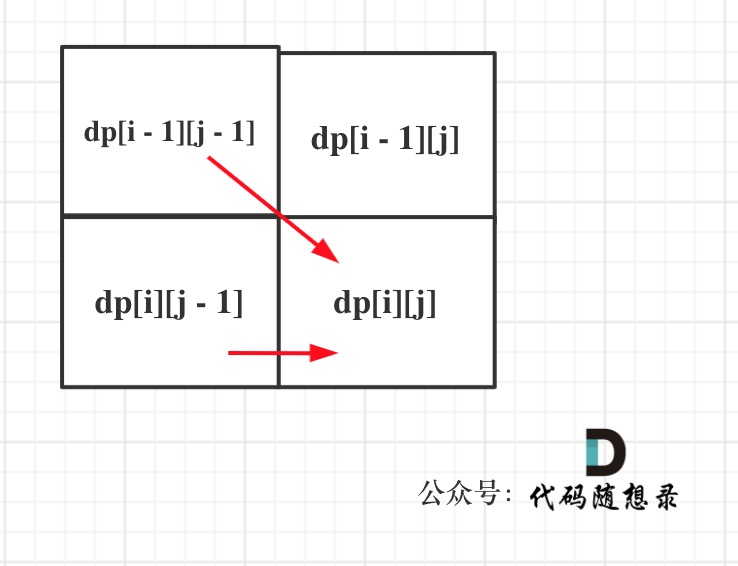
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序也应该是从上到下，从左到右

如图所示：

• 举例推导dp数组

以示例一为例，输入：s = "abc", t = "ahbgdc"，dp状态转移图如下：

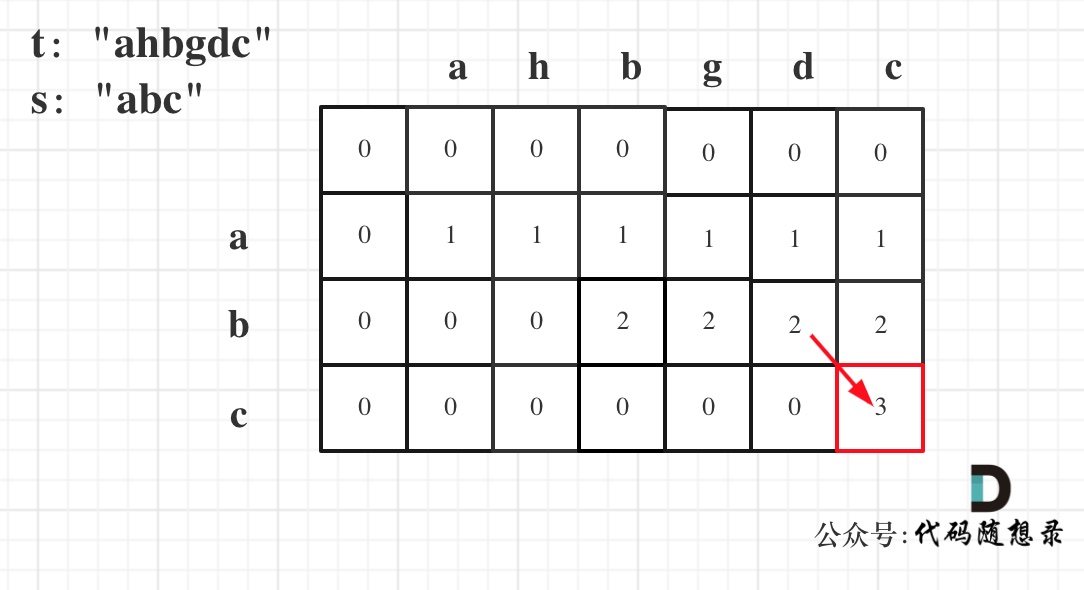
dp[i][j]表示以下标 i-1 为结尾的字符串 s 和以下标 j-1 为结尾的字符串 t 相同子序列的长度，所以如果 dp[s.length()][t.length()] 与字符串 s 的长度相同说明：s 与 t 的最长相同子序列就是 s，那么 s 就是 t 的子序列。

图中dp[s.length()][t.length()] = 3， 而s.length() 也为3。所以 s 是 t 的子序列，返回true。

动规五部曲分析完毕，Java代码如下：

java">class Solution {public boolean isSubsequence(String s, String t) {int length1 = s.length(); int length2 = t.length();int[][] dp = new int[length1+1][length2+1];for(int i = 1; i <= length1; i++){for(int j = 1; j <= length2; j++){if(s.charAt(i-1) == t.charAt(j-1)){dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = dp[i][j-1];}}}if(dp[length1][length2] == length1){return true;}else{return false;}}
}

• 时间复杂度：O(n × m)
• 空间复杂度：O(n × m)

总结

这道题目算是编辑距离的入门题目（毕竟这里只是涉及到减法），也是动态规划解决的经典题型。

这一类题都是题目读上去感觉很复杂，模拟一下也发现很复杂，用动规分析完了也感觉很复杂，但是最终代码却很简短。

编辑距离的题目最能体现出动规精髓和巧妙之处，大家可以好好体会一下。